Закономерности изменения физико-механических свойств семян

После определения признака, по которому отличаются компоненты смеси, и соответствующего рабочего органа, с помощью которого их можно разделить, встает вопрос о выборе рабочего размера элемента, отделяющего одни частицы от других. Например, если семена основной культуры имеют длину 8 мм, а у сопутствующего сорняка ‑ 4 мм, то их можно разделить в триерном цилиндре с размером рабочего элемента (ячейки), предположим, 5 мм. Но поскольку размеры семян (да и все другие физические признаки) являются случайными величинами, то выбор рабочих элементов часто становится затруднительным. Допустим, что длина семян основной культуры изменяется в пределах от 5 до 10 мм, а у сорняков ‑ от 3 до 8 мм. Возникает по меньшей мере два вопроса: возможно ли разделение смеси по данному признаку (длине семян) и какой диаметр ячейки триера следует выбрать, чтобы засоренность семян основной культуры хотя бы не превышала допустимых пределов.

Для ответа на эти вопросы нужно знать закономерность изменчивости размеров семян, т. е. уметь определять относительное количество мелких, крупных семян и т.д. Разумеется, поскольку размер каждого конкретного семени случаен, то при исследовании его изменчивости речь может идти лишь о вероятности появления семян с теми или иными размерами.

Связь между возможными значениями случайной величины и вероятностью их появления определяется законом распределения случайной величины.

Для непрерывной случайной величины X закон распределения F(x) определяет вероятность Р того, что случайная величина X окажется меньше заданного значения х:

F(x) = Р(Х < х)

Часто F(x) называют интегральной (суммарной) функцией распределения (рис. 6), которая очень удобна для вычислений вероятностных характеристик результатов очистки семян. С ее помощью легко определяется вероятность проходовой фракции, если задаться, предположим, размером отверстия решета х, или рассчитывается вероятность того, что размеры семян окажутся в каких-то пределах, допустим х...х+Dх. Вероятность этого события будет равна

F(x+Dx) ‑ F(x). (8)

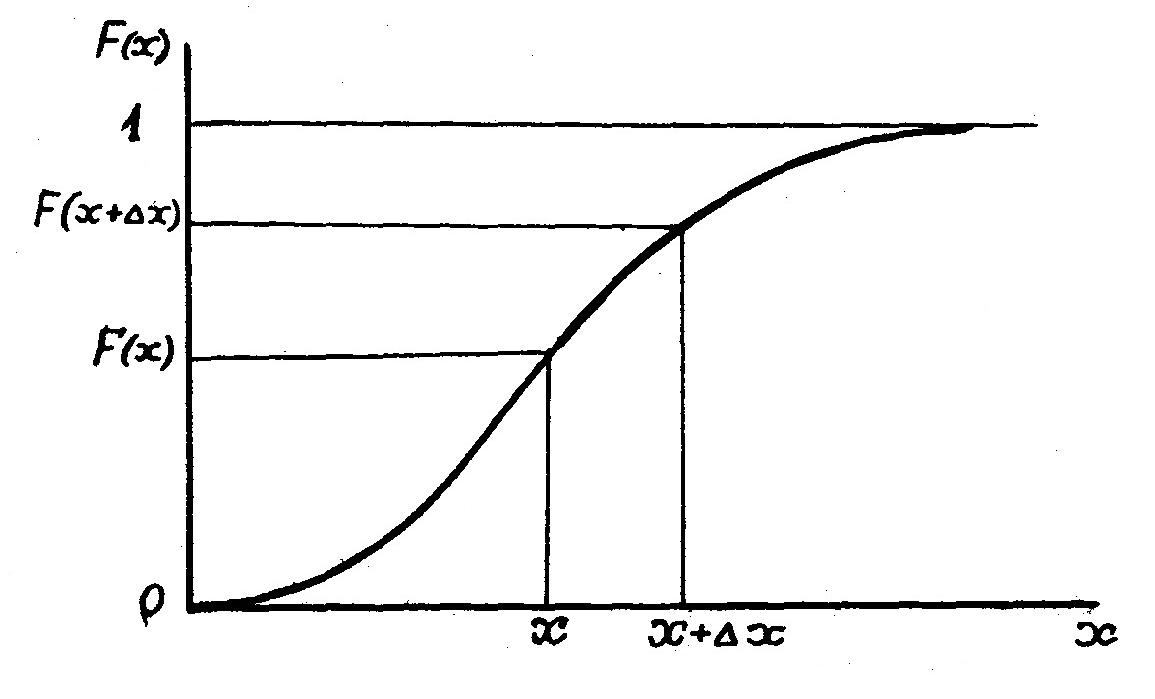
Рис. 6. Интегральная функция распределения случайной величины

К сожалению, интегральная функция не дает наглядной картины изменчивости ряда распределения. Трудно судить, глядя на график, каких семян больше, ‑ мелких, близких к среднему размеру или крупных.

Гораздо более наглядную картину изменчивости размеров семян дает дифференциальная функция распределения или, как ее еще называют, плотность распределения, так как она характеризует величину вероятности, приходящейся на единицу длины участка Dх.

В самом деле, вероятность того, что случайная величина X окажется на участке Dх, как только что было отмечено, равна

Р(х < Х < х + Dх) =F(x + Dx) ‑ F(x). (9)

Если найти отношение данной вероятности к длине участка Dх, т. е. определить среднюю вероятность, приходящуюся на единицу длины на этом участке, и перейти к пределу при Dх ®0, то

. (10)

Характерный вид дифференциальной функции распределения представлен на рис. 7.

Для того чтобы с помощью дифференциальной функции определить вероятность попадания случайной величины X на участок Dх, необходимо f(x) умножить на Dх, а если Dх ‑ достаточно большой интервал, скажем, от x₁ до х₂, то

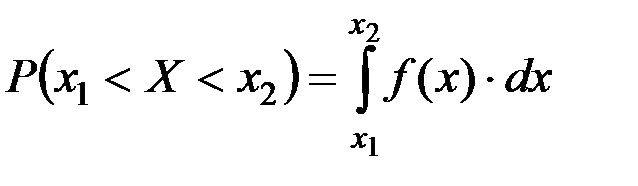, (11)

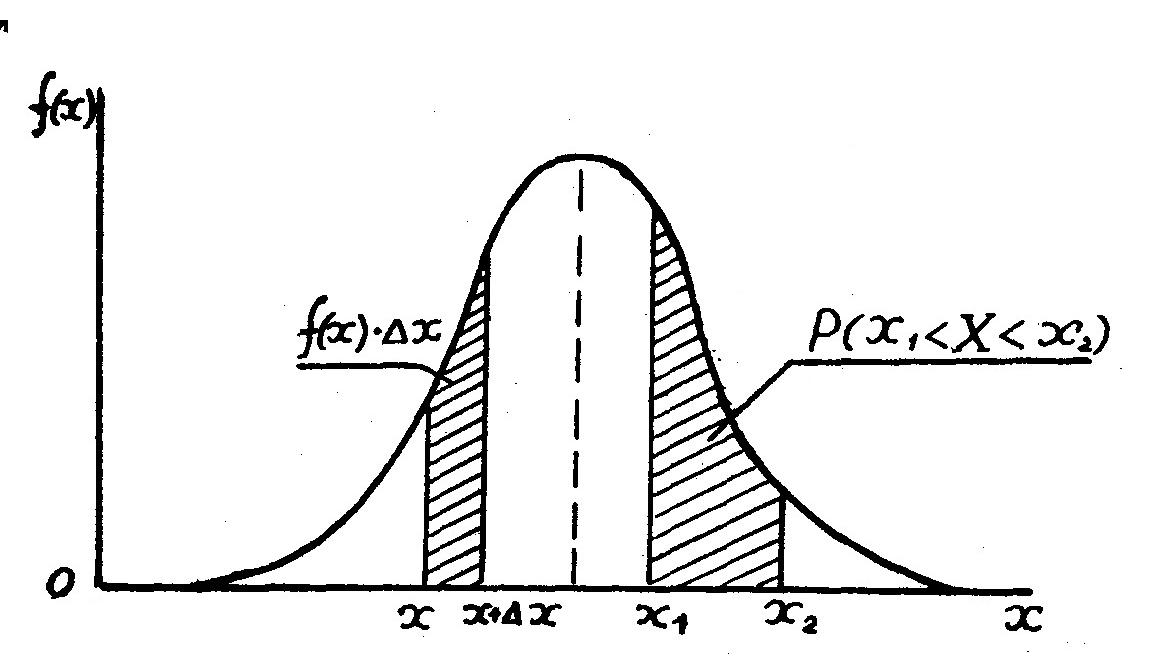
Рис.7. Дифференциальная функция распределения случайной величины

т. е. вероятность P(x₁ < Х < x₂) может быть представлена площадью, заключенной между осью х и кривой f(x) (рис. 7).

Таким образом, несмотря на то, что f(x) не является вероятностью, с помощью этой величины вероятность попадания на определенный участок может быть определена, и она будет тем выше, чем больше плотность распределения. Вследствие этого графики дифференциальной функции часто называют вероятностными кривыми распределения, или вариационными кривыми.

Наблюдения за изменчивостью размеров и других физико-механических свойств семян показали, что с большей степенью достоверности она может быть описана нормальным законом распределения (законом Гаусса) [1, 2, 3].

Плотность распределения по этому закону

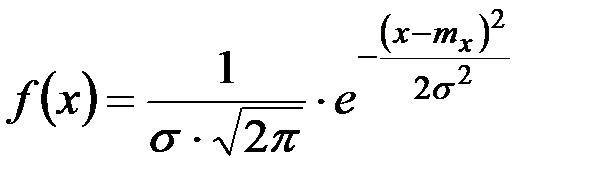, (12)

а интегральная функция

, (13)

где m_x, s ‑ числовые характеристики случайной величины;

m_х ‑ математическое ожидание;

s ‑ среднеквадратическое отклонение.

Поскольку числовые характеристики чаще всего приходится определять экспериментально, причем количество измерений существенно ограниченно, то при реальных расчетах их заменяют статистическими оценками:

, (14)

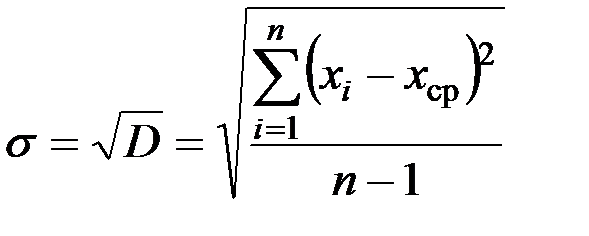. (15)

где D‑дисперсия случайной величины;

n ‑ число измерений.

Математическое ожидание или его оценка ‑ среднее значение ‑ часто именуют мерой положения случайной величины.

Вариационные кривые случайной величины с различными значениями х_ср занимают различные положения на оси х (рис. 8,а).

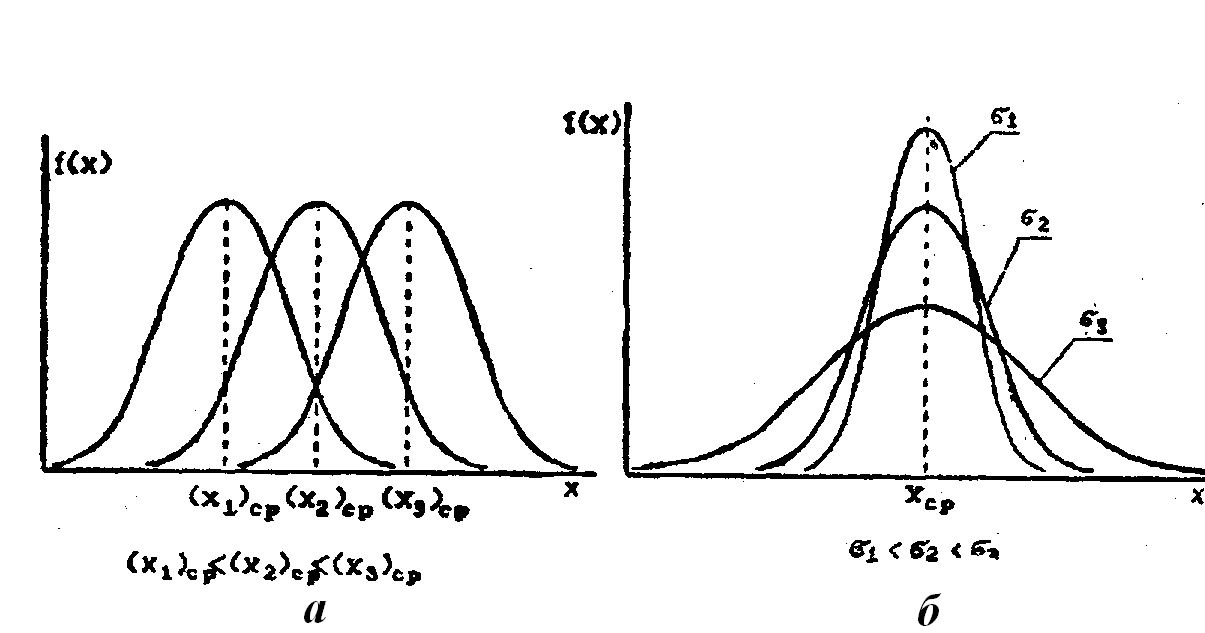
Рис. 8. Дифференциальные функции распределения при различных значениях числовых характеристик

Среднеквадратическое отклонение является мерой изменчивости случайной величины (рис. 8, б). Чем меньше s, тем: меньше отличаются фактические значения случайной величины от х_ср. С увеличением s вероятность значительных отклонений возможных значений случайной величины от х_ср возрастает.

Числовые характеристики физико-механических свойств семян многих культурных растений и сорняков приводятся в многочисленных литературных источниках по очистке и сортированию семян. Это дает возможность построения вариационных кривых свойств основной культуры и сопутствующих примесей, что позволяет обоснованно подойти к выбору принципа разделения смеси, размеров рабочих элементов и рассчитать вероятностные оценки результатов очистки по выбранной схеме.

Дата добавления: 2015-06-04