Приемы математико-картографического моделирования

Формализованное картографическое изображение хорошо при­способлено для математического анализа. Как упоминалось выше, каждой точке карты с координатами х и у поставлено в соответ­ствие лишь одно значение картографируемого параметра I, что позволяет представить изображение данного явления как функ­цию т. = Р(х,у). В других случаях картографическое изображение удобно представить как поле случайных величин и воспользовать­ся для его анализа вероятностно-статистическими методами.

В принципе почти все разделы математики применимы для обработки и анализа картографического изображения. Проблема лишь в том, чтобы точно подобрать математическую модель и, главное, дать надежное содержательное истолкование результатам моделирования. Достаточно прочно в картографический анализ вошли некоторые разделы численного анализа, многомерной ста­тистики, теории вероятностей и теории информации.

Аппроксимации. Под аппроксимациями в математике понимают замену (приближение) сложных или неизвестных функций другими, более простыми функциями, свойства которых известны. Любую слож­ную поверхность (поле), изображенную на изолинейной карте, можно аппроксимировать, т.е. приближенно представить в виде

г=/(х,у) + е,

где/(х, у) — некая аппроксимирующая функция, е — остаток, не поддающийся аппроксимации. Функцию /(х, у) можно далее раз­ложить в ряд, представив уравнение поверхности в виде

I =/,(*, У) +/₂(х, у) +... +/„ (х, у) + е, где /^х, у) — компоненты разложения, которые предстоит опреде-

лить. В общем случае для этого с аппроксимируемой карты снимают ряд значений г„ после чего составляют систему уравнений, решае­мых совместно по способу наименьших квадратов, т.е. так, чтобы 2е,² = 2 [Г(х_гу) -/(*,, у)У = тт.

Существуют разные способы аппроксимации. Это обычные ал­гебраические многочлены, ортогональные многочлены Чебышева и Лежандра, которые определенным образом упрощают вычисле­ния, сплайн-функции и др. Не останавливаясь на особенностях математического аппарата, отметим, что во всех случаях задача сводится к тому, чтобы аппроксимирующее уравнение наилучшим образом описывало исходную поверхность, а сумма квадратов от­клонений Ъ е.² была бы минимальна.

На рис. 12.16 показано последовательное улучшение аппрок­симаций на примере несложных поверхностей. Аппроксимация 1 -го порядка (линейное уравнение) дает плоскость, отражающую только общий уклон поверхности, это очень грубое, слишком общее приближение. Поверхность 2-го порядка уже больше похо­жа на исходную модель, а аппроксимация 3-го порядка (кубичес­кое уравнение) дает достаточно хорошее приближение к исход­ной поверхности.

Тригонометрические функции позволяют описывать сложные, сильно расчлененные поверхности, а сферические функции при­меняют, если при вычислениях нельзя пренебречь кривизной зем­ной поверхности. Аппроксимация с помощью двойных рядов Фу­рье, представленная на рис 12.17, иллюстрирует постепенное ус­ложнение поверхности за счет добавления двухмерных синусоид с разными фазами и амплитудами. Компьютерное моделирование позволяет выполнять подобные аппроксимации для поверхностей любой сложности, вычисляя уравнения высокого порядка, содер­жащие порой несколько десятков членов разложения.

В исследовательской практике аппроксимации используют для аналитического описания поверхностей (полей), изображенных на картах, и выполнения с ними различных действий: суммиро­вания, вычитания, интегрирования и дифференцирования, для подсчета объемов тел, ограниченных этими поверхностями, и ре­шения множества других задач. Одно из направлений использова­ния аппроксимаций — разложение поверхностей на составляю­щие, что позволяет выделять и анализировать нормальные и ано­мальные факторы развития и пространственного размещения явлений (см. разд. 13.2).

Глава XII. Методы использования карт

Приемы математико-картографического моделирования 231

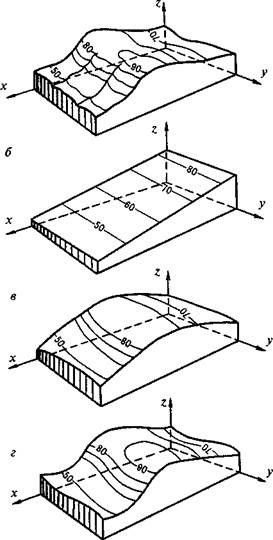
Рис. 12.16. Аппроксимации поверхностей:

а — блок-диаграмма исходной поверхности; б, в, г — блок-диаграммы аппрок­симирующих поверхностей соответственно 1, 2 и 3-го порядков.

Рис. 12.17. Схема тригонометрической аппроксимации поверхности с по­мощью последовательного наложения двухмерных синусоидальных волн (по Дж. Дэвису).

Приемы математической статистики. Эта группа приемов мате­матико-картографического моделирования предназначена для изу­чения по картам пространственных и временных статистических совокупностей и образуемых ими статистических поверхностей.

Глава XII. Методы использования карт

Приемы математико-картографического моделирования 233

-6-5-4 -3 -2 -1 0 +1

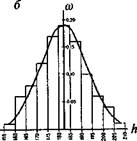
Рис. 12.18. Фрагмент карты рельефа (я) с сеткой точек регулярной вы­борки (выходы сетки отмечены на рамке), гистограмма и кривая рас­пределения высот (б): о — частость; А — высоты рельефа.

Статистический анализ картографического изображения пре­следует главным образом три цели:

♦ изучение характеристик и функций распределения явления;

♦ изучение формы и тесноты связей между явлениями;

♦ оценка степени влияния отдельных факторов на изучаемое явление и выделение ведущих факторов.

В основу всякого статистического исследования кладется вы­борка, т.е. некоторое подмножество однородных величин а., сня­тых с карты по регулярной сетке точек (систематическая выбор­ка), в случайно расположенных точках (случайная выборка), на ключевых участках (ключевая выборка) или по районам (райони­рованная выборка).

Выборочные данные группируют по интервалам, составляют гистограммы распределения (рис. 12.18) и затем вычисляют раз­личные статистики — количественные показатели, характеризу­ющие пространственное распределение изучаемого явления. Наи­более употребительные показатели — среднее арифметическое, среднее взвешенное арифметическое, среднее квадратическое, дис-

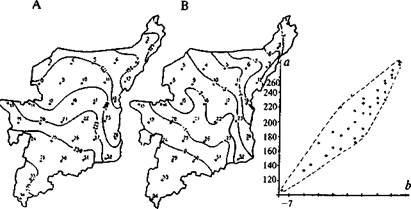
Рис. 12.19. Карты явлений и поле корреляции.

А — карта испарения с суши (мм/год) для территории Республики Коми; В — карта средней годовой температуры воздуха (°С) для той же территории.

персия, вариация и др. Кроме того, с помощью специальных по­казателей (критериев согласия) можно оценить соответствие дан­ного конкретного распределения тому или иному теоретическому закону распределения. Например, установить, согласуется ли эм­пирическое распределение высот рельефа с кривой нормального распределения, как это видно на рис. 12.18, или подчиняется ка­кой-то иной функции.

Другая типичная исследовательская задача — оценка взаимо­связи между явлениями — решается с помощью хорошо разрабо­танного в математической статистике аппарата теории корреляции. Для этого необходимо иметь выборки по сравниваемым явлени­ям, показанным на картах разной тематики (например, А и В). Значения а₎ и Ь, берут в одних и тех же 1-х точках, т.е. строго скоор­динировано, и затем строят график поля корреляции (рис. 12.19).

Если поле корреляции может быть аппроксимировано прямой, которая называется линией регрессии, то приступают к вычисле­нию коэффициента парной корреляции г. Его числовые значения заключены в интервале +1 > г > — 1. При г равном +1 или —1 существует функциональная прямая или обратная связь. Если г близок к 0, то связь между явлениями отсутствует, а при г > |0,7| связь считается существенной. Коэффициент корреляции рассчи­тывают по формуле

234 Глава XII. Методы использования карт

Приемы математико-картографического моделирования 235

2>,-лО(*,-лО

г =

"ЯР,,

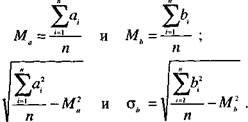
а =

где а₁ и Ь₁ — выборочные данные, полученные по картам А и В; п — объем выборки (число пар данных); М_ан М_ь — соответствую­щие значения средних, ао_аио,- средних квадратических.

Оценку точности вычисления коэффициента корреляции г

\-г

получают по формуле Щ - —г=-, из которой видно, что при

Ып

прочих равных условиях погрешность вычисления коэффициента корреляции всегда уменьшается с увеличением объема выборки. Отсюда следует, что определение объема выборки — важная про­блема при расчете коэффициента корреляции, да и вообще при вычислении всех статистических показателей. Достаточно предста­вительной обычно считается выборка объемом 30-50 значений.

В практике исследования взаимосвязей часто необходимо по­лучить предварительную приближенную оценку коэффициента корреляции. В простых случаях это можно сделать, используя пред­ставление о статистических поверхностях. Доказано, что коэффи­циент корреляции примерно равен косинусу угла а между направ­лениями наибольших скатов (градиентов) двух сравниваемых ста­тистических поверхностей

г ~ сов а.

Значения заключены в интервале соз 0° > г> соз 180°. Если а = 0°, что свидетельствует о полном совпадении направлений скатов по­верхностей, то г = соз 0° = 1, т.е. между явлениями существует

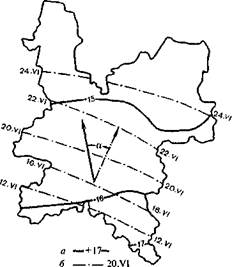
Рис. 12.20. Приближенное определение коэффициента корреляции по ко­синусу угла между направлениями наибольших скатов статистичес­ких поверхностей.

а — изотермы июля в Кировской области; 6 — изолинии дат начала цветения луговых трав.

прямая связь. При а = 180° скаты поверхностей направлены в про­тивоположные стороны, и г = соз 180° = — 1, следовательно, связь высока, но отрицательна, а при а = 90° связь между явлениями отсутствует, поскольку г = соз 90° = 0. На рис. 12.20 представлены две статистические поверхности и показаны направления их наи­больших скатов. Угол между ними оказался равен 36°, тогда г — = соз 36° = +0,81. Такие приближенные вычисления особенно удоб­ны при сравнении изолинейных карт.

Для оценки взаимосвязи явлений в случаях, когда трудно или невозможно получить большие выборки, используют другой по­казатель — ранговый коэффициент корреляции у, который вычис­ляют по формуле

■» - 1 и]

236 Глава XII. Методы использования карт

Приемы математико-картографического моделирования 237

где р_щ и р_ь. — ранги значений, полученных соответственно по кар­там А и В, т.е. их порядковые номера в возрастающей последова­тельности (1, 2, 3 и т.д.), а я — объем выборки.

По смыслу у аналогичен коэффициенту парной корреляции г, он изменяется в интервале от —1 до +1. При этом не требуется больших объемов выборки, расчеты можно выполнять даже при п = 3. К тому же не нужны точные количественные значения о,, и />,., достаточно знать их ранги. Все это удобно для работы с картог­раммами, где используются интервальные шкалы, а объем выбор­ки ограничен числом административных районов.

Аппарат теории корреляции достаточно разнообразен, в нем есть показатели, удобные для анализа взаимосвязей по картам аре­алов (где явления характеризуются только двумя состояниями: «есть» и «нет»), по картам качественного фона (где каждое явле­ние имеет много состояний, но не охарактеризовано количествен­но). Существуют коэффициенты для расчета криволинейных зави­симостей и связей между тремя явлениями (коэффициенты мно­жественной корреляции) и т.п.

Расчет корреляций дает основу для более сложных видов ана­лиза: регрессионного, дисперсионного, факторного и др. Часто при исследованиях ставится задача выделить основные факторы, опре­деляющие развитие и размещение того или иного явления. Эту задачу решает многомерный факторный анализ. Он позволяет све­сти к минимуму (к трем-четырем главным факторам) большие совокупности исходных показателей, характеризующих сложное явление. Уравнение факторного анализа имеет вид

л

а_р =Ъ1_рг/_г+е_р^

г = 1

где а — исходные показатели; /_г — выделенные главные факторы, дающие синтетическую оценку изучаемого явления; 1_рг — «вес» каждого фактора в этой синтетической оценке («факторная на­грузка»); е — остаток, характеризующий неучтенные отклонения.

Приемы теории информации. Эти приемы используют для оцен­ки степени однородности и взаимного соответствия явлений, изу­чаемых по картам.

Речь идет об основной функции теории информации — энтро­пии. В термодинамике энтропия характеризует степень беспорядка в физической системе, в теории связи — степень неопределенности

передаваемых сообщений, а в картографическом анализе эта функ­ция оказалась довольно удобной для оценки степени однородности/ неоднородности (разнообразия) картографического изображения.

Энтропией Е (А) некоторой системы А называется сумма про­изведений вероятностей со. различных состояний этой системы на логарифмы вероятностей, взятая с обратным знаком

п

Е(А) = Е(щ, со₂,..., со,,)=- X со,1о§ ₂ СО;

1=1

В теории информации принято брать логарифмы вероятностей при основании 2, что связано с двоичной системой счисления. Смысл функции не изменится, если пользоваться десятичными или натуральными логарифмами. Функция Е(А) остается неотри­цательной, она обращается в нуль, когда на карте изображен только один контур или выдел (т.е. изображение совершенно однородно), и монотонно возрастает с увеличением числа контуров п. Это свой­ство функции энтропии позволяет количественно характеризовать неоднородность картографического изображения (рис. 12.21), по­нимаемую как разнообразие контуров и неравномерность их рас­пространения по площади (различие величин со,).

Кроме того, информационные функции используют для оценки степени взаимного соответствия (совпадения) контуров на разных картах. В этом случае они выполняют роль своеобразных показателей взаимосвязи явлений наподобие коэффициентов корреляции.

гМ.) < Е(А,) < _Е(А₃) < г(*,)._т„

Рис. 12.21. Увеличение энтропии Е(А) с возрастанием числа контуров на карте (а) и изменением соотношения их площадей (б).

Изучение структуры 239

Глава XIII

Дата добавления: 2015-06-04