Теория механизмов и машин 1 страница

Ш Щ Э

Ц Ч

Ф

У

С

Р

П

О

Н

Л

К

И

Ж З

Е

B

Термины упражнений художественной гимнастики

Специфические термины упражнений на батуте

Кач – отдача сетки после прихода на неё прыгуна.
Подскоки – (темповые прыжки), применяемые для увеличения взлёта исполнителя.
Остальные термины образуются в соответствии с правилами гимнастической терминологии.

Шаги – разнообразные виды передвижения.
Различают: обычный шаг, шаг с носка, на носках, острый шаг, выпадами, шаг галопа, приставной шаг, переменный шаг, шаг польки и др.
Бег – передвижение шагами, в каждом из которых имеется фаза полёта.
Названия бега аналогичны видам ходьбы.
Поворот – вращательное движение тела вокруг вертикальной или продольной оси.
Различают: поворот переступанием (одноимённый, разноимённый), на носках, скрестный, махом, а также в приседе, в равновесии (с сохранением положения тела) и др.
Прыжок – свободный полёт после отталкивания ногами.
В зависимости от амплитуды движения и положения тела в воздухе различают: прямой прыжок, согнувшись, прогнувшись, открытый, закрытый, шагом, скачок, перекидной, подбивной, выпадом и др.
Пружинное движение руками – целостное пружинное движение со сгибанием во всех суставах.
Выполняется в различных направлениях.
Волна – сложное целостное движение, состоящее из последовательного разгибания в одних суставах и сгибания в других.
Различают: волну вперёд, вправо, влево (боковая волна).
Волна рукой – волнообразное движение рукой (руками), начинающееся сгибанием руки (к себе) и опусканием кисти, затем разгибанием (от себя) с одновременным подниманием кисти.
Положение кисти принято именовать так: обычное (не указывается), кисть свободна, кисть расслаблена, кисть поднята.

Валентное приближение – упрощающееприближение, в котором в расчет включают только валентные электроны (и орбитали). Полуэмпирические квантово-химические методы, такие как РМХ (EHT), ППДП (CNDO), МЧПДП (MNDO), AM1 и PM3, используют именно это приближение (в отличие отполновалентных методов аb initio).

Ван-дер-ваальсовы атомные радиусы – радиусы контактирующих атомов, которые определяют расстояния между молекулами, связанными ван-дер-ваальсовыми силами в кристаллах или в жидкостях. Определяются статистической обработкой данных рентгеноструктурного анализа в предположении, что радиусы либо аддитивны, либо для них справедливо среднегеометрическое соотношение. Квантово-химически ван-дер-ваальсовы атомные радиусы оценивают, как половину расстояния, на которое удалены атомы, энергия ван-дер-ваальсова взаимодействия которых равна 4 кДж×моль^-1 (типичная величина энергии).

Ван-дер-ваальсовы молекулы -слабо связанные молекулы в кластерах и молекулярных ассоциатах. Из-за слабых ван-дер-ваальсовых взаимодействий между частями системы имеют место большие амплитуды нулевых колебаний молекул относительно их положений равновесия, что ведет к большим структурным изменениям при вращательном и колебательном возбуждении.

Ван-дер-ваальсова связь – вид связи, обусловленной дисперсионными силами, индукционным взаимодействием и ориентационным взаимодействием. Энергия ван-дер-ваальсовой связи составляет 2–20 кДж∙моль^–1.

Ван-дер-ваальсовы силы -силы атомного и молекулярного взаимодействия при достаточно больших расстояниях между частицами. Связаны с корреляционными эффектами, вызванных флуктуациями наведенных дипольных моментов. Зависимость ван-дер-ваальсовых сил от расстояния и угловую зависимость взаимодействия несферических частиц представляют с помощью эмпирических выражений, таких как потенциалом Леннарда-Джонса (6-12).

ВЗМО (HOMO) -высшая занятая электронами молекулярная орбиталь. По теореме Купманса энергия ВЗМО молекулы приближенно равна потенциалу ионизации, взятому с обратным знаком.

Вибронные состояния – состояния молекул или кристаллов, определяемые неразделяемым взаимодействием электронной и ядерной подсистем. Возникают, когда энергия ядерных колебаний сопоставима с разностью энергий основного и возбужденных электронных состояний.

Волновая функция – функция координат частиц x_i и времени t Ψ (x₁, x₂, …,x_n, t) = Ψ ({x},t), полностью описывающая состояние системы n частиц. Волновая функция является решением уравнения Шредингера для рассматриваемой системы и содержит полную информацию о системе, позволяя определить пространственное расположение частиц, их импульсы, кинетическую энергию и т.д. Выражение Ψ^*({ x },t)Ψ({ x },t)d x имеет смыслвероятности того, что в момент времени t 1-я частица находится в интервале координат от x ₁ до x ₁+d x ₁, 2-я частица находится в интервале координат от x ₂ до x ₂+d x ₂, и т.д.

Вырождение – если две или несколько различных волновых функций системы соответствуют одной и той же энергии, говорят, что соответствующие им состояния системы вырождены. Так, три np -орбитали свободного атома образуют трехкратно вырожденную систему функций, а π-орбитали двухатомных молекул – двукратно вырожденный набор. Вырождение тесно связано с симметрией системы.

Вычислительная химия -область химии, задачей которой является компьютерное моделирование молекулярных систем для исследования их химического поведения и свойств. Использует методы, основанные на квантовой механике, классической механике и их комбинациях. Вычислительная химия - альтернатива химическому эксперименту в случаях, когда эксперимент является или невыполнимым, опасным или дорогостоящим.

Г
Гамильтониан -оператор полной энергии системы Н: H = T + V есть сумма операторов кинетической энергии T и потенциальной энергии V.

Гауссовы примитивы – индивидуальные функции гауссова типа, используемые в базисных наборах.

Гибридизация орбиталей –математический прием, широко применяющийся в структурной химии для соотношения геометрии молекул и системы их ковалентных связей. Гибридные орбитали представляют собой линейную комбинацию различных АО и описывают связи, внутренние электроны и неподеленные электронные пары. В общем случае гибридные АО неэквивалентны. Конкретный тип гибридизации АО диктуется геометрией молекулы, а также принципом максимального перекрывания орбиталей, согласно которому наиболее прочные связи образуются в направлении наибольшего перекрывания гибридных АО.

Глобальный минимум энергии – особая точка на поверхности потенциальной энергии (ППЭ), отвечающая самому глубокому минимуму. Характеризует наиболее устойчивую конфигурацию молекулярной системы. Остальным локальным минимумам ППЭ соответствуют изомеры с меньшей энергией. Особые точки ППЭ, не принадлежащие к глобальному или локальным минимумам, соответствуют неустойчивым геометрическим конфигурациям молекулярной системы (например, переходным состояниям).

Градиент потенциальной энергии – первая производная потенциальной энергии молекулярной системы по ядерным координатам. Точки ППЭ, в которых градиент энергии равен нулю, отвечают глобальному или локальному минимуму или переходниму состоянию конфигурации молекулярной системы.

Групповые орбитали -комбинации АО лигандов, которые, благодаря своим свойствам симметрии, формируют МО с подходящими по симметрии орбиталями металла-комплексообразователя.

Граничная орбиталь – понятиеодной из теорий реакционной способности, опирающейся на идею, что оптимальными местами атак в реакциях являются атомы, имеющие максимальную электронную плотность некоторых орбиталей. В случае электрофильной реакции граничная орбиталь - ВЗМО (HOMO), в случае нуклеофильной реакции - НСМО (LUMO).

Д
Дативные связи – химические связи, образованные путем передачи электронов с заполненных AO лигандов на вакантные s-орбитали центрального атома комплекса и частичным обратным перетоком электронов на p-орбитали лиганда. Это, например, имеет место в гексакарбониле хрома Сr(СО)₆: происходит смещение пары электронов от лиганда к иону металла через s-связь (s-донирование или донорно-акцепторная связь) и частичный обратный переток электронов к лиганду через p*-связь (обратное p-донирование или дативная связь).

Детерминант Слейтера – детерминант, построенный из ортонормированных спин-орбиталей - атомных или молекулярных. Позволяет получить приближенную многоэлектронную волновую функцию N электронов, обеспечивая ее правильные антисимметричные свойства. Элементы детерминанта Слейтераесть описывающие электроны орбитали и перестановка электронов эквивалентна перестановке местами столбцов (строк) детерминанта, что изменяет его знак:

.

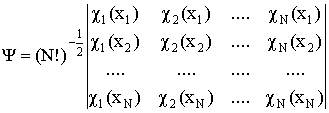Используется в методах Хартри-Фока, Кона-Шэма и др.

Деформационная электронная плотность есть разность между электронной плотностью молекулы (вычисленной или определенной экспериментально при помощи дифракции рентгеновских лучей) r_мол(r) и суммой электронных плотностей отдельных атомов, расположенных там же, где и ядра в реальной молекуле rå_атом (r): rd(r) = r_мол(r) - rå_атом (r). Функцию rå_атом обычно называют промолекулой. Позволяет в концентрированном виде представить, как изменилось электронное распределение при образовании молекулы из атомов. Различают стандартную (промолекула есть совокупность атомов со сферически усредненными ЭП) и химическую (промолекула из несферических атомных ЭП, адаптированных к симметрии окружения) деформационные электронные плотности.

Дипольный момент молекулы – количественная характеристика электронного строения молекулы, когда распределения положительного и отрицательного зарядов не совпадают. Используя матрицу зарядов-порядков связей, можно вычислить дипольный момент молекулы с помощью выражения ,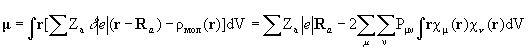

где ρ _мол – электронная плотность, P_μν – элементы матрицы зарядов-порядков связей, R_a – радиусы векторы ядер. Дипольный момент нейтральной молекулы не зависит от выбора начала отсчета. Дипольные моменты молекул определяются измерением комплексной диэлектрической проницаемости как функции частоты и температуры, из ИК спектров и с помощью других методов.

Дисперсионные силы – составляющие сил межмолекулярного ван-дер-ваальсова взаимодействия, обусловленные взаимодействием мгновенных индуцированных диполей. Возникают из-за корреляции во флуктуациях распределений электронной плотности соседних молекул. Энергия дисперсионного взаимодействия характеризуется зависимостью от межмолекулярного расстояния R^-6, что находит отражение в межмолекулярном потенциале Леннарда-Джонса (6-12).

Диффузные функции - базисные функции, отвечающие возбужденным состояниям атомов. Включаются в расчет для того, чтобы описать электронную оболочку отрицательно заряженных молекул и электронные эффекты на большом расстоянии от ядра.

Естественные орбитали – орбитали φ_ν (r), удовлетворяющие уравнению на собственные значения матрицы плотности первого порядка ρ(r | r ´): ∫ ρ(r | r ´) φ _ν (r ´) d r ´ = n_ν φ _ν (r). Вероятность пребывания электрона в состоянии, определяемом функцией φ_ν (r), характеризуется естественной электронной заселенностью n_ν. Матрица плотности первого порядка для естественных орбиталейдиагональна, а электронные заселенности равны 0, 1 или 2. Вычисления с использованием конфигурационного взаимодействия для естественных орбиталей сходятся быстрее.

Запрещенная зона – промежуток на энергетической шкале между верхней энергетической зоной, заполненной электронами (валентной), и нижней, не заполненной электронами (зоной проводимости) в твердом теле. В запрещенной зоне нет энергетических уровней.

Изодесмические реакции -химические реакции, в которых сохраняется конфигурация химических связей.

Индексы реакционной способности (ИРС) –электронные и энергетические характеристики, полученные в результате квантово-химических расчетов, которые коррелируют с экспериментальными данными о реакционной способности.Практическое применение ИРС следует рассматривать в плане образования набора расчетных величин – дескрипторов, коррелирующих с конкретными свойствами молекулярной системы. Примерами распространенными ИРС являются: валентность атома и кратность связей, молекулярный электростатический потенциал, абсолютная жесткость и абсолютная мягкость молекулярных систем, энергия активации реакции разрыва химической связи и др.

Инерциальные оси молекулы - три оси, определяющие моменты инерции молекулярной системы. Зависят от положений и масс атомов. Первая инерционная ось обычно отмечает самый протяженный размер молекулярной системы, а третья ось - самый короткий.

Интеграл перекрывания – количественная характеристика суммарного эффекта интерференции двух волновых функций 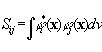. Равен нулю, если суммарный эффект отсутствует (интерференции не происходит или эффекты интерференционного усиления и ослабления равны). В случае полной интерференции (когда орбиталь взаимодействует сама с собой) S_ij=1. Орбитали с нулевым интегралом взаимного перекрывания называются ортогональными. Чем больше величина интеграла перекрывания атомных орбиталей, тем больше отличие энергии образующейся молекулярной орбитали от суммы энергий исходных атомных орбиталей и тем шире энергетические полосы в твердых телах.

Ионные связи – химическиесвязи с асимметричным распределением электронной плотности. Ионные связи имеют ненулевые значения дипольного момента.

Квантовая механика - Теория движения и взаимодействий микрочастиц. В квантовой химии поведение электронов в поле фиксированных ядер и химические свойства соединения чаще всего описывают с помощью уравнения Шредингера. Принято считать, что поведение электронов можно описать ограниченным числом приближенных одноэлектронных функций - орбиталей, причем каждая орбиталь характеризуется специфическими размерами, формой и энергией. Электроны имеют корпускулярные и волновые свойства; орбитали, учитывая волновые свойства, позволяют вычислить вероятность нахождения электрона в определенном месте пространства.

Квантовые числа электрона в атоме – состояние электрона в атоме характеризуется четырьмя квантовыми числами. Главное квантовое число n = 1, 2, 3, … ∞ характеризует энергию электрона в атоме. Орбитальное квантовое число l = 0, 1, 2, … (n-1) характеризует орбитальный момент количества движения электрона. Магнитное квантовое число + l, +(l-1), -1 < m_l < 1…, -(l-1), -l характеризует величину проекции орбитального момента количества движения на ось Z. Магнитное спиновое квантовое число m_s определяет ориентацию спинового углового момента относительно некоторой оси. Принимает значения +1/2 и -1/2. Cпиновое квантовое число - s, определяет величину собственного момента импульса. Принимает значение +1/2.

Ковалентные связи – химические связи, образованные атомами путем обобществления электронной плотности. Ковалентные связи, образованные одинаковыми атомами в двухатомных молекулах имеют нулевые значения дипольного момента.

Конформационный анализ – исследование возможных пространственных конфигураций атомов, отвечающих локальным минимумам на ППЭ, переходы между которыми не сопровождаются разрывом или образованием химических связей. Возможные индивидуальные конфигурации атомов в пространстве называются конформерами, конформационными изомерами или ротамерами. Для экспериментального изучения строения твердых тел используют методы дифракции рентгеновских лучей, электронов и нейтронов, веществ в растворенном и газообразном состоянии - методы молекулярной спектроскопии ИК, КР, ЯМР.

Конформация молекулы с минимальной энергией (англ. МЕС) - точка в энергетическом конфигурационном пространстве, в которой энергия молекулы имеет абсолютный минимум. Все производные энергии по координатам в этой точке равны нулю и диагональные элементы матрицы вторых производных (матрицы Гессе) положительны.

Компьютерный дизайн -компьютерный поиск новых молекул, обладающих теми или иными свойствами, до их синтеза. Использует элементы информатики, статистики, математики, химии, физики, биологии и т.д. Пример - компьютерный дизайн фармакологических препаратов с потенциальной терапевтической ценностью, которые удовлетворяют широкому диапазону количественных критериев: высокой активности, высокой избирательности, минимальной токсичности, высокой биологической совместимости.

Контрактация (группировка, сжатие) – построение базисных функций g в виде линейной комбинации гауссовых примитивов G_i: g = åа_iG_i. Каждая атомная орбиталь аппроксимируется линейной комбинацией построенных таким образом сгруппированных (контрактированных) ОГT (CGTO или СОГТ) т.е. c= åс_ig_i. Каждая СОГТ имеет свои собственные фиксированные коэффициенты и экспоненциальные множители. Использование контрактации уменьшает время вычисления интегралов, которое в методе Хартри-Фока зависит от 4-ой степени числа базисных функций.

Координата реакции – единственная нормальная координата в сечении ППЭ, вдоль которой переходное состояние между долиной исходных веществ и долиной продуктов есть локальный максимум (вдоль остальных координат переходное состояние – минимум). Переходное состояние отвечает седловой точке на ППЭ.

Корреляционная диаграмма - диаграмма, показывающая, в какие состояния объединенного и разъединенных атомов переходит данная МО при изменении межъядерного расстояния.

Кратность связи по Герцбергу есть ,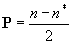

где n и n* - число электронов на соответственно связывающих и разрыхляющих МО. Согласуется с химическими представлениями о характере связей в гомоядерных молекулах.

Кристаллические орбитали – математическая функция, которая зависит от пространственных координат одного электрона и описывает поведение электрона в кристалле. По аналогии с молекулярными орбиталями кристаллические орбитали j _k (r) строятся из базисных функций, роль которых играют одноэлектронные функций Блоха u _{k j}(r): j _k (r) = å c_j(k) u _{k j}(r).

Кулоновское взаимодействие -электростатическоевзаимодействие зарядов по закону Кулона.

Кулоновский интеграл – интеграл, описывающий классическое электростатическое взаимодействие электронов на орбиталях.

Локализованные молекулярные орбитали (ЛМО) - описывают электроны остова, локализованные на связях, неподеленные электронные пары и т.д. Строятся из канонических МО j_j с помощью ортогонального преобразования f_i =åА_ijj_j. Обычно требуют, чтобы новые ЛМО отвечали критерию òò f_i² (1/r_ij) f_j² = min, для каждой пары электронов i и j. Кулоновское взаимодействие электронов на одной и той же ЛМО максимально, а обменное взаимодействие между электронами на разных ЛМО минимально.

Локальный минимум энергии - минимум на энергетической поверхности для молекулярной системы, представляющей конформацию с самой низкой потенциальной энергией. Вычисления, направленные на оптимизацию геометрической конфигурации молекулярной системы, обычно оканчиваются на конфигурации, соответствующей локальному минимуму энергии.

М
Матрица Гессе (Hessian matrix) -матрица частных вторых производных целевой скалярной функции f(x).

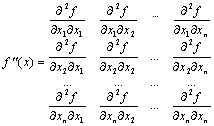
Частный случай - матрица вторых производных от потенциальной энергии по ядерным координатам. Диагонализация матрицы Гессе позволяет определить нормальные моды колебаний и вычислить колебательные частоты.

Матрица зарядов-порядков связей – матрица, элементами которой являются величины 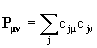, где c_jμ, c_jν – коэффициенты в разложении МО ЛКАО для μ и ν-ой атомных орбиталей в j-ой молекулярной орбитали (суммирование ведется по занятым МО). Играет важную роль в теории химической связи, приближенно описывая распределение электронной плотности в молекуле, дипольный момент и т.д.

Межмолекулярные взаимодействия – взаимодействия между молекулами, которые определяют механизм столкновений молекул, некоторые стадии химических реакций, а также существование молекулярных жидкостей и твердых тел и их свойства: термодинамические и кинетические характеристики, энергию сцепления, равновесную геометрию, фононные спектры и др. Обусловлены слабыми дальнодействующими силами, их энергии лежат в пределах 1-40 кДж/моль. Описываются либо квантово-химической теорией возмущения, либо полуэмпирическим методом атом-атомных потенциалов.

Метод Кона-Шэма – основной метод теории функционала плотности. Основан на предположении, что электронную плотность можно рассматривать как неоднородный электронный газ. Одноэлектронные уравнения имеют вид (атомные единицы): [ -1/2Ѳ + V_N(r) +rò(r ¢)/(r- r ¢)d r ¢ +V_xc ] j _k (r) = E(k)j _k (r), где V_N –потенциал ядер, V_xc – обменно-корреляционный потенциал, для которого используются различные приближения – функционалы ЭП. Базисные функции различны: это могут быть наборы атомных орбиталей или плоских волн, а также их комбинации. Недостаток: недооценка ширины запрещенной зоны в твердых телах.

Метод конфигурационного взаимодействия (КВ или CI) – один из методов, позволяющих учесть энергию электронной корреляции. Многоэлектронная волновая функция в этом методе раскладывается в ряд по детерминантам Слейтера, описывающим систему во всех возможных электронных конфигурациях. Каждый такой детерминант строится из спин-орбиталей, отвечающих основному или одному из возбужденных одноэлектронных состояний. Полная КВ волновая функция, учитывающая все возможные электронные возбуждения, имеет вид: 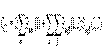и ищется вариационным путем. При этом спин-орбитали в каждом слейтеровском детерминанте сохраняют неизменными, что предполагает их предварительный расчет методом Хартри-Фока, а варьируют коэффициенты а_k. Метод применим к описанию возбужденных состояний, систем с открытыми оболочками и неравновесных систем (например, диссоциирующих молекул), фотохимических реакций.

Метод наискорейшего спуска – является одной из распространенных процедур минимизации дифференцируемой функции нескольких переменных. Согласно этому методу после вычисления в начальной точке градиента функции делают шаг в направлении антиградиента, и движутся до тех пор, пока функция убывает. Достигнув точки минимума на выбранном направлении, снова вычисляют градиент функции и повторяют описанную процедуру. При этом градиент вычисляется только при смене направлений движения. Метод хорошо "работает" при минимизации гладких функций и если начальное приближение выбрано достаточно далеко от минимума. Если же очередная точка окажется в окрестности минимума, то уменьшение целевой функции будет очень медленным из-за того, что для получения минимума с высокой точностью необходимо выполнить большое число мелких шагов. Слабыми местами метода является медленная сходимость и эффективность только при поиске точек локального минимума.

Метод Ньютона-Рафсона – метод многомерной оптимизации для нахождения экстремума целевых функций многих переменных с использованием производных. Предполагается, что функция дважды дифференцируема, строится линейная аппроксимация производной функции в начальной точке, а точка, в которой аппроксимирующая линейная функция обращается в нуль, принимается в качестве следующего приближения. В зависимости от выбора начальной точки и вида функции алгоритм метода Ньютона-Рафсона может как сходиться к истинной стационарной точке, так и расходиться.

Метод Парризера-Попла-Парра – использует совместно приближение нулевого дифференциального перекрывания и π-электронное приближение. Параметры метода эффективно включают в себя учет конфигурационного взаимодействия. Хорошо зарекомендовал себя как при определении геометрии, потенциалов ионизации и сродства к электрону, так и при расчетах оптических спектров поглощения плоских сопряженных органических молекул.

Метод сопряженных градиентов -как и метод наискорейшего спуска, является методом локальной оптимизации. Отличается высокой надежностью при поиске точки минимума из удаленной исходной точки и быстро сходится в окрестности точки минимума. В основе метода лежит процедура построения сопряженных направлений, для получения которых применяется квадратичная аппроксимация целевой функции и значения компонент градиента. Получил применение в области оптимизации благодаря широкому классу проблем, для которых он обеспечивает сходимость к оптимальному решению за конечное число шагов. Это серьезное улучшение по сравнению с методом наискорейшего спуска, который требует бесконечного числа итераций для поиска минимума функции

Метод Частичного Пренебрежения Дифференциальным Перекрытием (INDO) – использует приближение нулевого дифференциального перекрывания (НДП) при вычислении двухэлектронных кулоновских и обменных интегралов, которое, однако, не действует в отношении одноцентровых обменных интегралов. Последние сохраняются и вычисляются аналитически, явно учитывая угловую зависимость АО. Это - полуэмпирический метод ССП. Полезен для вычисления электронных свойств основного состояния систем с открытыми и закрытыми оболочками, изучения спиновых плотностей, оптимизации геометрии и общей энергии. Для вычисления энергетических состояний молекул, содержащих переходные металлы, можно использовать метод ZINDO/1, основанный на измененной версии INDO/1. Для воспроизведения ультрафиолетовых и видимых спектральных переходов, используется другая модификация - ZINDO/S, при параметризации которой учтены однократно возбужденные электронные конфигурации.

Метод модифицированного пренебрежения двухатомным перекрыванием (MNDO) - полуэмпирический метод ССП. Более корректно описывает отталкивание неподеленных электронных пар за счет учета всех двухэлектронных интегралов, содержащих пары атомных орбиталей одного и того же атома, перекрывание атомных орбиталей различных атомов игнорируется (пренебрежение двухатомным дифференциальным перекрыванием). Параметры зависят только от свойств отдельных атомов, а не от их парных комбинаций. Применим для различных органических молекул, содержащих элементы из длинных строк 1 и 2 из периодической таблицы, но не переходные металлы. Вычисляет электронные свойства, оптимизированные конфигурации, общую энергию и теплоты образования.

Минимальный базисный набор -наименьший набор орбиталей в квантово-химических вычислениях, состоящий только из функций, которые необходимы для размещения всех электронов атома в основном состоянии. Минимальный базисный набор для атома углерода: 1s, 2s, 2p_x, 2p_y, 2p_z. Минимальные базисные наборы не описывают детали молекулярных электронных распределений.

Минимизация энергии молекулы -процедура поиска минимальной молекулярной энергии для определенной точки в конфигурационном пространстве. Часто сопровождается оптимизацией геометрии молекулы. Существуют различные алгоритмы оптимизации (например, наискорейшего спуска, сопряженных градиентов, Ньютона - Рафсона).

Дата добавления: 2015-06-04