Основные определения теории множеств

ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ

V. Доказать

IV. Доказать

III. Доказать

II. Преобразовать к приведенной КНФ

I. Доказать общезначимость

1.

2.

3.

4.

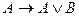
5.

6.

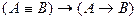
7.

8.

9.

10.

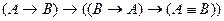
11.

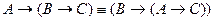
12.

1.

2.

3.

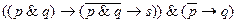
4.

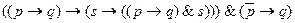
5.

6.

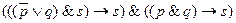
7.

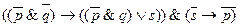
8.

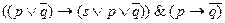
9.

10.

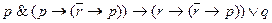
11.

12.

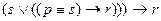
1.

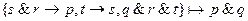
2.

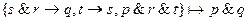
3.

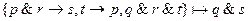
4.

5.

6.

7.

8.

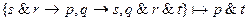
9.

10.

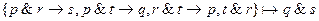
11.

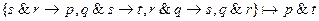
12.

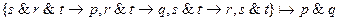
1.

2.

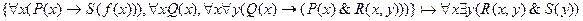
3.

4.

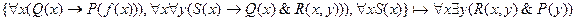
5.

6.

7.

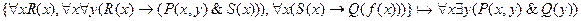
8.

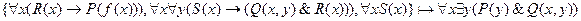
9.

10.

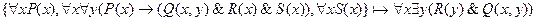
11.

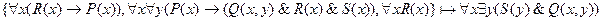
12.

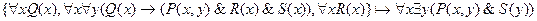
1.

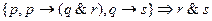
2.

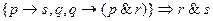
3.

4.

5.

6.

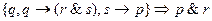
7.

8.

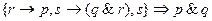
9.

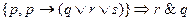
10.

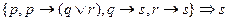
11.

12.

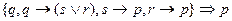
VI. Вычислить при всех значениях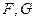

1. □ 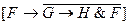; ◊ 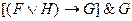при H =0

2. □ 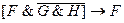; ◊ □ при H = 0

3. □ 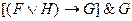; ◊ 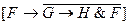при H = 0

4. □ □ ; ◊ при H = 0

5. □ 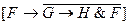; ◊ 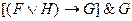при H = 1

6. □ ; ◊ □ при H = 1

7. □ 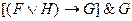; ◊ 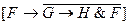при H = 2

8. □ □ ; ◊ при H = 2

9. ◊ ; ◊ □ при H = 0

10. ◊ ; ◊ □ при H = 1

11. ◊ 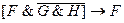; ◊ □ при H = 2

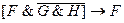12. □ ; ◊ □ при H = 2

Под множеством принято понимать совокупность объединенных по общим признакам различных предметов. Множества будем обозначать прописными латинскими буквами A, B,C, …, X, Y, Z, а элементы, принадлежащие данным множествам – строчными a, b, c, …, x, y, z. Если a есть элемент множества A, то пишут 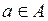. Если a не является элементом множества A, пишут . Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается Æ. Рассматриваемое исходное множество называется универсальным и обозначаются U. Если все элементы множества A являются также элементами множества B, то говорят, что А включается в B или A является подмножеством множества B и обозначается . Если , то говорят, что A=B или A совпадает с B.

Диаграмами Ейлера-Вена называються фигури, с помощью которых изобрахают на плоскости множества и наглядно демонстрируют свойства операций над множествами. Прямоугольник на плоскости означает некоторое универсальное множество, которое включает в себя рассматриваемые множества.

Рисунок 1. Диграма Ейлера- Вена.

Объединением двух множеств A и B называется множество, составленное из элементов, входящих хотя бы в одно из данных множеств, оно обозначается . Соответствующая диаграмма Ейлера- Вена:

Рисунок 2. Объединение двух множеств.

Объединением некоторой совокупности множеств называется множество S, составленное из всех элементов, входящих хотя бы в одно из слагаемых множеств 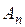, и обозначаемое .

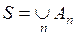Пересечением двух множеств A и B называется множество, составленное из всех элементов, принадлежащих как множеству A, так и множеству B, и обозначается . Соответствующая диаграмма Ейлера- Вена:

Рисунок 3. Пересечение двух множеств.

Два множества A и B называются непересекающимися, если их пересечение пусто.

Пересечением некоторой совокупности множеств называется множество P, составленное из всех элементов, входящих во все множества 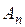, и обозначаемое .

Разностью двух множеств A и B называется множество, составленное из всех тех элементов множества A, которые не принадлежат множеству B. Разность обозначается A\B.

Рисунок 4.Разность двух множеств

Прямым (или декартовым) произведением двух множеств A и B называется множество всевозможных пар (x, y), где . Произведение множеств A и B обознначается .

Дополнением к множеству A называется множество , состоящее из элементов универсального множества, U не принадлежащих множеству A, т.е. .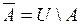

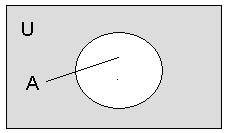
Рисунок5. Дополнение к множеству A

Операции над множествами имеют следующие свойства:

1. Коммутативность: .

2. Ассоциативность: .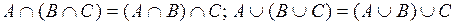

3. Дистрибутивность: .

4. Законы де Моргана: .

Дата добавления: 2015-06-04