Методические указания к решению задач

Основные определения и обозначения

Перестановки и сочетания с повторениями

До сих пор мы рассматривали предметы, которые были попарно различны. А теперь рассмотрим совокупности, в которых имеются одинаковые предметы.

Пусть имеются предметы k различных типов, число предметов первого типа равно 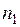, второго типа - 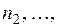k- го типа -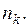

Число различных перестановок, которые можно сделать из даных элементов, равно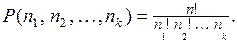

Число m – элементарных подмножеств, порядок в которых не принимается во внимание, равно

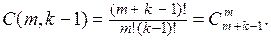
Применять формулы перестановок и сочетаний с повторениями следует в том случае, когда объекты выбираются из совокупности, имеющей одинаковые предметы.

Пример 13. Сколько различных перестановок можно сделать в слове МАМА?

Решение. Если бы все буквы в слове были различны, то число всевозможных перестановок равнялось бы 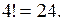Но поскольку в слове МАМА имеются одинаковые буквы, то перестановок получится меньше – некоторые перестановки совпадают друг с другом.

Например, возьмем перестановку АМАМ. Буквы А можно переставить между собой, но такая перестановка ничего не меняет. То же самое можно сказать относительно букв М. Таким образом, различных перестановок будет 24: 6. Выпишем их: МАМА, МААМ, ММАА, ААММ, АММА.

Пример 14. В почтовом отделении продаются открытки десяти видов. Сколькими способами можно купить в нем 12 открыток?

Решение. В данном случае нужно выбрать подмножество, состоящее из 12 элементов, порядок элементов в котором несущественен, и среди выбранных элементов обязательно будут одинаковые. Таким образом, число способов выбора открыток равно числу сочетаний с повторениями C(m, k-1), причем k = 10, m=12:

.

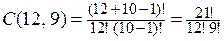Пример 15. Найти число всех таких слов длины mn в n – буквенном алфавите, в которых каждая буква алфавита встречается m раз.

Решение. Число слов равно числу перестановок с повторениями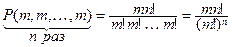

Пример 16. Сколькими способами множество из n элементов может быть разбито на S подмножеств, из которых первое содержит 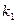элементов, второе - 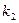элементов, …, s – e - 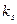- элементов.

Число способов равно числу перестановок с повторениями

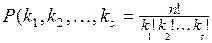
Литература

1. Н. Я. Виленкин. Комбинаторика. ¾ М.: Наука, 1969.

2. И. И. Ежов, А. В.Скороход, М. И. Ядренко. Элементы комбинаторики. ¾ М.: Наука, 1977.

3. К. А. Рыбников. Введение в комбинаторный анализ. ¾ М.: МГУ, 1972.

Дата добавления: 2015-06-04