Масштабом топографических карт называется отношение длины линии на карте к длине горизонтальной проекции соот­ветствующей линии на местности

При небольших уклонах (небольшом угле а) длины линий на местности практически совпадают с их проекциями — горизонталь­ным проложением. Поэтому можно считать масштабом в этих слу­чаях отношение длины линии на карте к длине соответствующей линии на уровенной поверхности.

На картах масштаб указывается за южной рамкой и дается в трех видах: численный, именованный и линейный (рис. 16).

Численный (числовой) масштаб выражается дробью, у ко­торой в числителе — единица, а в знаменателе — число М, пока­зывающее степень уменьшения горизонтального проложения на

карте. Например:------> или 1:10 000. Следует четко и ясно понять

и запомнить, что в числителе и знаменателе этой дроби числа да­ны в сантиметрах. В числителе 1 см — это длина линии на карте, а в знаменателе 10 000 см — это длина этой же (соответствующей) линии на местности в сантиметрах. (Если уклон линии значитель­ный, то 10 000 см — длина горизонтального проложения, т. е. про­екции этой линии.)

Таким образом, масштаб — это степень уменьшения длин линий (или их горизонтальных проложений) при изображении этих линий на карте.

Так, на карте масштаба 1:100 000 длина линий уменьшена относительно их горизонтальных проекций в 100 000 раз. Или 1 см длины на карте соответствует линия на местности длиной 100 000 см.

Численный масштаб сопровождают пояснением, указывающим соотношение длин линий на карте и на местности; при этом рас­стояние на местности указывается не в сантиметрах, а в метрах или километрах. Такой пояснительный масштаб называется имено­ванным.

Рис. 16. Три вида масштаба

Например, если численный масштаб 1:100 000, то именованный к нему: «в 1 см на карте —1 км»; если численный масштаб 1:10 000, то именованный: «в 1 см —100 м».

Все знают, что в 1 м —100 см, а в 1 км —1000 м, но научить­ся переводить численный масштаб в именованный и наоборот не­обходимо решением многочисленных задач. Задачи могут быть та­кого типа: «В 1 см —5 км. Каков численный масштаб карты?» Необходимо перевести километры в метры. Переведем в метры 5 км. Это будет 5000 м, затем в сантиметры: 5000 м = 500 000 см. Та­ким образом, численный масштаб будет 1:500 000. Подобным об­разом решаются обратные задачи перевода численного масштаба в именованный.

Следует обратить внимание на чтение масштаба, т. е. на пра­вильное произношение числительных. Например, масштаб карты — одна двадцатипятитысячная (1:25 000), а не «одна двадцать пять тысячная».

Линейный масштаб служит для определения по картам длин линий с помощью измерителя или линейки. Пользуясь линей­ным масштабом, можно сразу измерить расстояние на карте в сан­тиметрах, метрах и километрах, не прибегая к вычислениям. Ли­нейный масштаб представляет собой две прямые линии, между которыми примерно 2 мм, разделенные на равные отрезки (а). Эти отрезки выбираются произвольно, однако так, чтобы было удобно выполнять измерения, т. е. они должны быть кратными привычным нам десятичным числам (1 км, 100 м). Для повышения точности определения расстояния крайний слева отрезок делится на 10 бо­лее мелких частей (Ь). Равные отрезки, откладываемые вправо от нуля, называются основанием масштаба; одно такое основание отложено влево от нуля и разделено, как указывалось уже, на 10 частей. Это наименьшее деление масштаба.

Все три вида масштаба: числовой, именованный и линейный — помещаются за южной рамкой карты и являются ее обязательным вспомогательным элементом оформления.

То расстояние на местности, которое соответствует наименьше­му делению линейного масштаба (0,1 см), называется точностью масштаба.

Предельная точность масштаба обусловлена свойствами человеческого зрения. Разрешающая способность глаза в среднем 0,1 мм, и она считается графической точностью карты. Таким об­разом, предельная точность измерений по карте равна величине в метрах, соответствующей 0,01 см в масштабе данной карты.

Пример. Определить масштаб карты, если графическая точность измерения по карте 5 м. Рассуждаем: в 0,1 мм —5 м, в 1 мм — 50 м, в 1 см — 500 м. Следовательно, масштаб данной карты 1:50 000.

Масштаб площадей — это отношение площади фигуры на карте (1 см²) к площади горизонтальной проекции соответствую­щего участка местности. Он равен квадрату масштабов длин. Как

правило, масштабы площадей выражаются словесно, так как циф­ры в основании велики. Так, если числовой масштаб 1:25 000, то масштаб площадей будет 1:250 000² = 1:625 000 000.

Различают крупные и мелкие масштабы. Чем крупнее масштаб, тем будет подробнее и детальнее картографическое изображение (карта). Зато при мелком масштабе на карте можно изобразить большую по площади территорию, но с меньшей подробностью.

На топографических картах искажения, обусловленные кривиз­ной Земли, не имеют значения, так как не ощущаются графичес­ки. Это позволяет измерять по картам расстояния, площади и уг­лы. Такие возможности карты имеют очень большое значение, поскольку позволяют решать по ней различные инженерные зада­чи, получать количественные характеристики отдельных природных или социальных объектов.

Для определения расстояния по прямой линии между двумя точ­ками необходимо взять с карты это расстояние по линейке или из­мерителем и определить его с помощью линейного масштаба либо надо измерить в сантиметрах отрезок между двумя точками, а по­том, зная масштаб карты (т. е. сколько метров содержится в 1 см карты), определить искомое расстояние в метрах.

Пример. Линия между точками А и В на карте имеет длину 10 см. Масштаб карты 1:10 000. Чему равно это расстояние на ме­стности?

В 1 см карты —100 м расстояния на местности. Линия АВ равна 10 см. Следовательно, расстояние на карте будет равно- 10 см х хЮО м = 1000 м = 1 км.

Часто требуется измерять на карте расстояние по кривым ли­ниям: рекам, дорогам, границам. В этом случае плавные кривые измеряют как отрезки ломаных прямых линий малым раствором циркуля (2 — 4 мм) (рис. 17). Зная масштаб карты и общую дли­ну ломаной линии, определяют величину расстояния на местно­сти.

Иногда для измерения кривых линий пользуются прибором кур­виметром (рис. 18). Колесико прибора катят по измеряемой кри-

Рис. 17. Измерение расстояний циркулем: а — способом наращивания раствора циркуля; б — шагом циркуля

вой, а система передач сообщает это движе­ние стрелке. По шкале на циферблате опре­деляют расстояние, пройденное колесиком на карте (в сантиметрах или в метрах).

Длины, измеренные по карте, всегда со­держат некоторую ошибку. Чем крупномас­штабнее карта, тем точнее измерения по ней.

Измерение площадей объектов по карте (озер, полей, массивов леса и т. п.) произ­водят разными способами. Все они, как пра­вило, приближенные.

Если участок ограничен прямыми линия­ми, то его делят на простые фигуры, суммар­ная площадь которых легко определяется. Это могут быть квадраты, прямоугольники, треугольники и т. п.

Чаще всего площади измеряют с помо­щью палетки — прозрачной пластинки с сеткой квадратов на ней. Площадь квадратов известна. Палетку накладывают на измеряе­мый контур и считают число квадратов вну­три его. Площадь неполных квадратов оценивается на глаз. Чем меньше площадь квадрата палетки, тем точнее измерения площади. Наконец, ориентировочно определить площадь можно на глаз, пользуясь километровой сеткой карты.

Рис. 18. Курвиметр

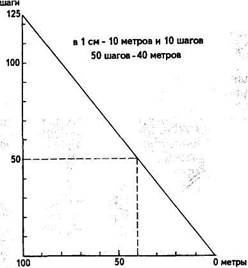
Рис. 19. Клиновой масштаб

Существует прибор, с помощью которого площади по картам измеряют достаточно точно: это планиметр.

К вопросу измерения по картам относится и перевод одних ли­нейных мер в другие. Это требуется при работе с картами, сделан­ными в разных мерах длины, или если надо построить карту в ме­трах, а расстояние измерено, например, шагами. В таких случаях строится график перехода одних мер в другие — клиновой мас­штаб. По горизонтали откладываются метры, например 100 м (в 1 см —10 м), а по вертикали — шаги (другая мера), число кото­рых соответствует 100 м (рис. 19). Причем откладывается эта ве­личина в том же масштабе, что и по вертикали. Концы катетов со­единяются. С помощью гипотенузы осуществляется переход из одних мер в другие.

Понятия: масштаб числовой, масштаб именованный, масштаб линейный, масштаб площадей, основание масштаба, предельная точность масштаба, курвиметр, палетка.

На память.

Русские меры длины: сажень —3 аршина —2,134 м; верста —500 саженей, т. е. немного больше 1,0668 км; вершок —4,45 см; аршин —0,711 м (в аршине 16 вершков).

Английские меры длины: дюйм —25,4 мм; фут —12 дюймов —304,8 мм; ярд — 3 фута —36 дюймов —91,44 мм; миля сухопутная —1760 ярдов —5280 футов — 1609 м; морская миля —1852 м.

4.2.2. ПРОЕКЦИЯ ТОПОГРАФИЧЕСКИХ КАРТ. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ

Топографическая карта представляет собой изображение не­большого участка земной поверхности. На топографической круп­номасштабной карте искажения на кривизну Земли практически от­сутствуют.

При картографировании большой по площади территории неиз­бежно будет сказываться кривизна Земли, и это приведет к иска­жениям на карте.

Для того чтобы избежать ощутимых искажений на топографи­ческих картах, применяется поперечная цилиндрическая проекция Гаусса — Крюгера. Сущность ее заключается в том, что, во-пер­вых, осуществляется проектирование поверхности земного эллип­соида на боковую поверхность цилиндра. Проектирование осуще­ствляется по зонам, имеющим протяженность 6° долготы. Во-вторых, цилиндр разрезается по образующей, и зона становит­ся плоским двуугольником.

Представьте себе касательный к эллипсоиду цилиндр, располо­женный таким образом, что малая ось эллипсоида перпендикуляр­на оси цилиндра (рис. 20). Будем проектировать поверхность эл­липсоида на боковую поверхность цилиндра узкими двуугольниками, заключенными между меридианами с разницей долгот в 6°— так

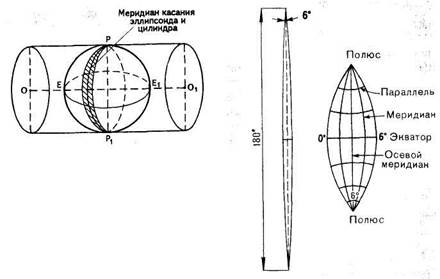
Рис. 20. Взаимное расположение зем­ного эллипсоида и цилиндра: РР_Х — малая ось цилиндра; 00, — ось ци­линдра; ЕЕ_Х — экватор. Заштрихован­ная зона — сферический двуугольник

Рис. 21. Схематическое изображение зоны Гаусса — Крюгера на плоскости

Рис. 22. Координатные зоны и их нумерация

называемыми зонами Гаусса — Крюгера (рис. 21). При этом цилиндр касается эллипсоида по его меридиану, и эта линия у них общая — меридиан касания. Он сохраняет свою длину и не имеет искажений при переходе на боковую поверхность цилин­дра и, следовательно, при его последующей развертке в плос­кость. По экватору протяжен­ность зоны с запада на восток примерно 666 км. Меридиан, который проходит посредине зо­ны, называется осевым.: он дей­ствительно для двуугольника является осью симметрии.

Таким образом, проектируют­ся все 60 зон (360°: 6° = 60 зон), каждая на отдельный ци­линдр. При развертке цилиндра в плоскость получается плоское изображение зоны в проекции Гаусса — Крюгера (поперечной цилиндрической). Это изобра­жение зоны схематически пока­зано на рисунке 22. В действи-

тельности зона очень узкая полоса, ширина которой на экваторе в 30 раз меньше ее длины, так как от полюса до полюса зона имеет 180°, а по долготе всего лишь 6°.

Осевой меридиан и экватор изображаются в проекции без ис­кажений своей длины взаимно перпендикулярными линиями. Дли­на остальных меридианов искажена по мере удаления от осевого, но искажение не превышает величину 0,0014, т. е. величина иска­жения настолько мала, что не ощущается графически. Поэтому и считают, что топографические карты не имеют искажений, по ним можно делать любые картометрические измерения.

Границами зон служат меридианы. Зоны нумеруются арабскими цифрами от Гринвичского меридиана к востоку. Первая зона, таким образом, заключена между 0° и 6° в. д. (рис. 21), вторая зона нахо­дится между 6° и 12° в. д. и т. д.— всего 60 зон.

Прямоугольные координаты определяют положение точки на плоскости, в зоне Гаусса — Крюгера, и показывают по­ложение точки относительно экватора и осевого меридиана в ки­лометрах (рис. 23).

В каждой зоне осями координат служат проекция линии эк­ватора и свой осевой меридиан. Они взаимно перпендикулярны. Осевой меридиан зоны принят за ось X. (В первой зоне его долгота 3° в. д., во второй зоне 9° в. д. и т. д.) Линия экватора принята за ось Y. Положение любой точки в зоне определяется координатами X и Y. X — это расстояние в километрах от экватора до точки, a Y — расстоя-

Дата добавления: 2015-06-04