Введение

МАТЕМАТИКА

РЕГИОНАЛЬНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ

НВУЗ АНО

Дополнительная

Основная

1. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. М.: Наука, 1980.

2. Берман Г.Н. Сборник задач по курсу математического анализа. М.: Hаука, 1981, 1971.

3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1, 2. М.: Высшая школа, 1980.

1. Эльсгольц Л.Э Дифференциальные уравнения и вариационное исчисление. М.: Высшая школа, 1969.

2. Степанов В.В. Курс дифференциальных уравнений. М.: Гостехиздат, 1953.

3. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. М.: Наука, 1973.

СОДЕРЖАНИЕ

1. Основные понятия и определения. Простейшие типы дифференциальных уравнений..................................3

2. Линейные дифференциальные уравнения первого порядка.

Уравнение Бернулли..........................................11

3. Уравнения в полных дифференциалах. Интегрирующий множитель. 16

4. Особые решения дифференциальных уравнений. Огибающая семейства интегральных кривых. Уравнения Клеро и Лагранжа. Другие типы дифференциальных уравнений, решаемых методом введения параметра..........................................22

5. Дифференциальные уравнения старших порядков.................29

6. Линейные дифференциальные уравнения...................... 35

7. Метод вариации произвольных постоянных. Уравнение Эйлера. Линейные дифференциальные уравнения с переменными коэффициентами.............................................45

8. Системы дифференциальных уравнений........................54

9. Метод Эйлера интегрирования систем линейных дифференциальных

уравнений...................................................59

10. Литература................................................. 68

ИНСТИТУТ»

(Четвертая лекция)

_______________________________

http://elearning.rfei.ru

Содержание

ВВЕДЕНИЕ………………………………………………………….3

РАЗДЕЛ 1. О КОМБИНАТОРИКЕ И ТЕОРИИ

ВЕРОЯТНОСТЕЙ........................................................................ 4

Глава 1.1. Основные понятия комбинаторики........................ 4

Глава 1.2. Размещения............................................................. 9

Глава 1.3. Размещения с повторениями................................ 10

Глава 1.4. Сочетания и их свойства..................................... 122

Глава 1.5. Сочетания с повторениями................................... 14

Глава 1.6. Понятие вероятности события............................ 155

Глава 1.7. Аксиомы теории вероятностей........................... 222

Глава 1.8. Основные теоремы теории вероятностей........... 266

Глава 1.9. Формула полной вероятности............................ 301

Глава 1.10. Биномиальное распределение.......................... 322

Глава 1.11. Случайные величины и их числовые характеристики 344

РАЗДЕЛ 2. ВЫСШИЕ НАГРАДЫ В ОБЛАСТИ

МАТЕМАТИКИ....................................................................... 444

Вы приступаете к рассмотрению последней лекции курса математики. В ней вам предстоит познакомиться с комбинаторикой и элементами теории вероятностей.

Методы теории вероятностей широко применяются в различных отраслях естествознания, техники, и в частности, в экономике. Это направление науки служит для обоснования математической статистики, которая используется при планировании и организации производства, предупредительном контроле качества продукции и для многих других целей.

В последние годы в связи с широким распространением информационных технологий теория вероятностей и математическая статистика все шире и глубже проникают в различные области науки, техники, производства – в подтверждение мысли о математике – бензине двигателя под названием «Разум».

РАЗДЕЛ 1. О КОМБИНАТОРИКЕ И ТЕОРИИ ВЕРОЯТНОСТЕЙ

Глава 1.1. Основные понятия комбинаторики

Раздел, к рассмотрению которого мы приступаем, выделился в отдельную предметную область, но для студентов нематематических специальностей он рассматривается в общем курсе математики, что мы сейчас и пытаемся сделать, но с углублением в историю этого раздела.

Вначале выясним, что такое комбинаторика. Комбинаторика занимается различного рода сочетаниями (соединениями), которые можно образовать из элементов некоторого конечного множества. Термин «комбинаторика» происходит от латинского слова «combina» — сочетать, соединять.

Основными понятиями комбинаторики являются перестановки, размещения и сочетания. Термин «комбинаторика» стал употребляться после опубликования Лейбницем в 1666 г. работы «Рассуждение о комбинаторном искусстве», в которой впервые дано научное обоснование теории сочетаний и перестановок. Изучением «размещений» впервые занимался Якоб Бернулли во второй части своей знаменитой книги «Искусство предугадывания», опубликованной в 1713 г.

Познакомимся с основными понятиями комбинаторики через рассмотрение задач.

В знаменитой басне Крылова «Квартет» «проказница Мартышка, Осел, Козел да косолапый Мишка» устроили любопытный эксперимент — они исследовали влияние взаимного расположения музыкантов на качество исполнения. И если бы не вмешался Соловей, участники квартета, наверное, перепробовали бы все возможные варианты. Зададимся вопросом: сколько существует способов, чтобы рассадить, например, в один ряд, четырех музыкантов?

Другой случай. Воспетый Маяковским «мо-лоткастый, серпастый» советский паспорт имел серию и номер, состоящие в общей сложности из трех частей:

· некоторое число, записанное римскими цифрами;

· две русские буквы;

· шесть арабских цифр.

Например, IХ-РГ № 062993. Разумеется, все паспорта должны иметь разные номера. Сколько может быть различных паспортов?

Третья ситуация. Нас приглашают сыграть в «Лото-миллион». Суть игры в том, что нужно из 49 номеров угадать 6, которые выпадут во время тиража. Для участия в игре следует приобрести специальную карточку и вычеркнуть в ней 6 любых квадратов, пронумерованных числами от 1 до 49. Чтобы выиграть наверняка, можно было бы запастись таким количеством карточек, какое необходимо для вычеркивания 6 номеров всеми возможными способами. Сколько этих способов?

Общее у всех трех задач то, что их решением занимается отдельная область математики, называемая комбинаторикой. «Особая примета» комбинаторных задач — вопрос, который всегда можно сформулировать так, чтобы он начинался словами: «Сколькими способами…».

Пусть имеется несколько объектов, неважно каких, лишь бы все они различались между собой: книги, детские кубики или музыканты крыловского «Квартета». Мысленно расставим их в ряд и такое упорядоченное расположение объектов назовем перестановкой. Попытаемся ответить на вопрос: сколько всего возможно перестановок из предметов? Число перестановок обозначают 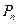подчеркивая тем самым, что оно зависит от количества предметов .

Попытаемся найти 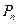сначала для небольших . Если 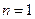, т. е. имеется один-единственный предмет, то существует и один-единственный способ его расстановки. Поэтому 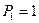. Возьмем 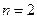. Сразу понятно, что 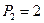, поскольку два предмета (назовем их А и Б) можно расставить двумя различными способами: АБ и БА. Попробуем рассуждать несколько иначе: первый предмет (А) установим неподвижно, а второй (Б) будем «прилаживать» к нему. Безусловно, объект Б можно поставить либо спереди, либо сзади от А, следовательно, число перестановок 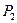вдвое больше, чем , т.е. 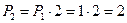. Добавим теперь третий предмет В. К каждой из перестановок двух объектов А и Б можно пристроить третий предмет тремя различными способами: поставить его спереди, между ними либо сзади. Перестановка АБ, таким образом, порождает три перестановки: ВАБ, АВБ и АБВ, перестановка БА — также три: ВБА, БВА и БАВ, и все получившиеся шесть перестановок — разные. Отсюда .

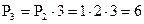Вообще, из каждой перестановки 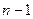предметов можно получить дополнительных перестановок, добавляя -й предмет либо спереди, либо сзади, либо между имеющимися предметами (между 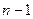предметами существует 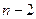промежутка; 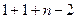— вот и выходит ровно ). Стало быть, при переходе от 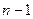к предметам количество перестановок увеличивается в раз. Поэтому общая формула будет такой:

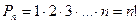. (1.1)

Восклицательным знаком (в математике он называется факториалом) принято обозначать произведение всех натуральных чисел от 1 до включительно.

Мы не просто вывели формулу, но одновременно указали способ, как получить все возможные перестановки. Надо отметить, что он далеко не единственный. Например, все перестановки можно получить из начальной, поочередно меняя местами соседние объекты.

Современная символика сочетаний была предложена разными авторами учебных руководств лишь в XIX в. В частности, знак факториала (!) был введен в 1808 г. в одном французском учебнике Хр. Крампа. Термин же «факториал» был образован от слова «фактор» (множитель) происходящего от латинского factor — производящий.

А теперь вернемся к решению задачи о квартете. Четыре горе-музыканта из басни Крылова долго пересаживались с места на место. В ходе этого «творческого поиска» Осел внес предложение: «Мы, верно, уж поладим, коль рядом сядем». Попробовали — не помогло. Но в ряд-то можно сесть по-разному! Давайте определим число возможных перестановок. Здесь 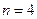, поэтому способов «усесться чинно в ряд» имеется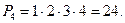

Добавим, что для решения некоторых задач приходится применять идею перестановок не в «чистом» виде, а с поправками. Допустим, главный фактор, влияющий на качество игры, — это соседи каждого музыканта, и не важно, кто из них справа, а кто слева. При таком условии перестановка «Мартышка, Осел, Козел, Мишка» эквивалентна зеркально-симметричной: «Мишка, Козел, Осел, Мартышка». Понятно, что в этом случае все 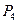вариантов разбиваются на пары равнозначных перестановок. И если из каждой пары оставить по одной перестановке, то общее число различающихся вариантов будет .

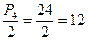Теперь представим, что музыканты сели не в ряд, а по кругу. В этом случае можно рассуждать так: в каждом из вариантов пронумеруем всех участников по часовой стрелке, начиная, скажем, с Осла. В различных перестановках каждый музыкант, конечно, должен иметь разные номера. Только у одного из них — Осла — будет постоянный номер 1. Значит, осталось пронумеровать различными способами только троих. Поэтому здесь число возможных перестановок —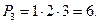

Есть особый (и очень важный!) вид перестановок — перестановки с повторениями. В них среди прочих участвуют предметы, неразличимые между собой, — «близнецы». Замена одного «близнеца» другим не приводит к новой расстановке. Предположим, что, отчаявшись, наши музыканты решили создать вместо квартета симфонический оркестр. Для этого Мартышка привела с собой еще 15 мартышек, Осел — еще 20 ослов, Козел — 10 козлов, лишь Мишка поленился и остался в одиночестве. Выясним, сколькими способами можно рассадить их в ряд.

Возьмем любую произвольную расстановку всех 49 музыкантов. Если бы «близнецов» в их числе не оказалось, то перестановок было бы 49! Но вот среди них появилось 16 одинаковых Мартышек. Не трогая остальных зверей, а меняя местами лишь Мартышек всеми возможными способами (а их будет 16!), получим вроде бы новые перестановки, но теперь уже неразличимые. То есть каждые 16! старых перестановок преобразуются в одну новую и общее число перестановок уменьшается в 16! раз. Очевидно, та же история и с ослами, и с козлами (лишь медведь по-прежнему один). В итоге количество перестановок окажется равным:

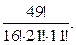
Медведя мы не учитывали, но, дабы не нарушать единообразия, добавим и его, т. е. поделим указанное выражение еще на 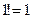, что ничего не меняет. А записывать это принято так:

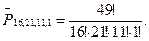
Обратите внимание на горизонтальную черту над буквой Р: с ее помощью отличают случай с повторениями от обычных перестановок.

Нетрудно получить и общую формулу для случая, когда имеется групп «близнецов», состоящих соответственно из 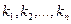неразличимых предметов:

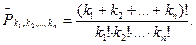(1.2)

Множество факториалов в этой формуле кого-то может смутить. Но в комбинаторике факториал — частый гость, даже хозяин. При его вычислении необходимо находить произведение последовательных натуральных чисел, что при большом значении числа 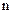не является простой задачей. Поэтому на помощь приходит либо инженерный калькулятор (что уже становится редкостью), либо встроенный в компьютер калькулятор. На калькуляторе функция «факториал» обычно обозначается символом , поэтому при практических расчетах вызывают вначале число, а затем нажимают на клавишу .

Воспользоваться калькулятором в компьютере можно с помощью команд меню «Пуск». Выбрав в главном меню пункт «Программы» ® «Стандартные» ® «Калькулятор» ® «Вид» и установите флажок на команду «Инженерный».

Факториал числа можно вычислить и с помощью уже известного вам программного продукта MS Excel. Для этого обратившись к Мастеру функций входят в категорию «Математические» и в ней выбирают функцию «ФАКТР», далее в диалоговое окно вводят нужное число. На рис. 1.1. вычислено значение в программе MS Excel.

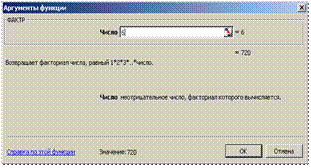
Рисунок 1.1

Глава 1.2. Размещения

Дата добавления: 2015-06-04