Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э

Иногда бывает нужно из имеющихся различных объектов отобрать произвольные штук () и расположить их в некотором порядке. Каждое такое упорядоченное расположение называется размещением. Сколько существует размещений при заданных и? Оказывается, ответ можно дать, основываясь на знании перестановок.

Обозначим искомое число . Сначала возьмем любую перестановку всех объектов и рассмотрим первые из них. Они образуют размещение объектов из имеющихся, тогда как последние 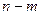объектов совершенно не влияют на это размещение, как их ни переставляй. Но эти 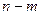«хвостовых» объектов могут быть переставлены 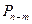способами. Значит, каждому размещению можно «пришить» 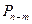различных «хвостов», что порождает столько же перестановок всех объектов. Общее число перестановок всех объектов 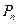в таком случае равно произведению искомого числа и : .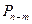

Отсюда:

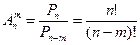. (1.3)

Общее число размещений можно рассчитывать и пользуясь теоремой, которая сводится к формуле:

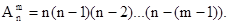(1.4)

Согласно записанной теоремы число размещений равно произведению 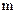сомножителей, начиная от 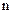и заканчивая

Предположим, что проходит некий конкурс с 8 участниками. Одновременно проводится викторина: нужно угадать, кто займет в конкурсе 1, 2 и 3-е места. Сколько всего существует вариантов ответов? Очевидно, что искомое количество равно числу размещений из 8 по 3, а это будет равно (по предыдущей теореме):

.

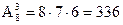Т. е. будет три сомножителя, начиная от 8 и последовательно уменьшая на единицу. Этот же результат получим, если воспользуемся формулой 1.3. Поэтому в зависимости от ситуации вы пользуетесь теоремой или формулой для определения числа размещений.

Мы уже говорили, что 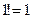, а как быть с числом нуль?

Как вы думаете, сколькими способами можно выбрать 0 объектов из имеющихся, или, другими словами, сколькими способами можно не выбрать ни одного объекта? Вопрос, конечно, странный, но формально получается:

.

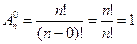Пожалуй, это логично: есть единственный способ не выбрать ни одного объекта из имеющихся — ничего не делать.

Второй вопрос: сколькими способами можно сделать упорядоченный выбор из объектов... всех ?

Поступаем так: выбираем любой объект, рядом с ним размещаем второй, потом третий и т. д. Получается обыкновенная перестановка всех объектов, и число таких перестановок .С другой стороны, согласно найденной формуле, это же число равняется:

Появилось новое выражение (факториал мы определяли только для натуральных чисел). Предположим, что — это какое-то неизвестное число, и найдем его из равенства .

Тогда 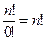, откуда 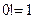, т. е. факториал нуля равен единице (хотя казалось, что это непременно должен быть нуль). Факториал нуля возникает в самых разных комбинаторных задачах, но везде и всегда его принимают равным единице.

Глава 1.3. Размещения с повторениями

Помимо обычных размещений бывают и размещения с повторениями (точно так же, как перестановки). Пусть имеется различных объектов. Выберем из них штук, действуя по следующему принципу. Возьмем любой, но не будем устанавливать его в какой-то ряд, а просто запишем под номером 1 его название, сам же объект после этого вернем к остальным. Затем опять из всех объектов выберем один (в том числе, возможно, и тот, который был только что изъят), запишем его название, пометив номером 2, и снова вернем объект обратно. И так далее, пока не получим названий. Размещения с повторениями обозначаются 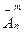. Оп ределить это число несложно. На первом месте в списке может находиться любой из объектов, на втором — тоже любой, и на третьем и на четвертом... в общем, на каждом. Поэтомучисло размещений с повторениями выражается формулой

(1.5)

Заметим, что здесь допустим случай, когда 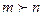, т. е. выбранных объектов больше, чем их всего имеется. Это неудивительно: каждый объект после «использования» возвращается обратно и может быть «использован» повторно.

Вернемся к решению задачи о паспортах. Определим, сколько может быть паспортов советского образца с различными сериями и номерами, если зафиксировать римские цифры серии. Остаются две русские буквы и шесть арабских цифр. Рассмотрим буквы и цифры отдельно.

В русском алфавите 33 буквы. Нам нужно выбрать любые две, при этом они могут оказаться и одинаковыми. Следовательно, имеет место размещение с повторениями, где 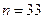и ,и, воспользовавшись предыдущей формулой, получим: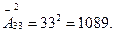

Что касается цифр, то здесь выбирается (и опять с повторениями) 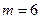цифр из возможных. Для этого есть 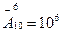способов.

Поскольку каждую пару букв можно соединить с любой шестеркой цифр, то возможно существование паспортов, имеющих одни и те же римские цифры серии, — больше миллиарда! Ну а если потребовать, чтобы в каждом номере и буквы, и цифры были различными, — сколько тогда получится паспортов? Здесь вместо размещений с повторениями нужно использовать обычные размещения. Поэтому ответ таков:

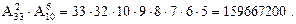
Сравните полученный результат с предыдущим. Число значительно уменьшилось, не правда ли?

Глава 1.4. Сочетания и их свойства

Индийцы умели вычислять числа, которые мы обозначаем через 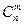, т. е. сочетания из элементов, взятых по .

Однако как научная дисциплина комбинаторика сформировалась лишь в XVII в.

В некоторых задачах по комбинаторике не имеет значения порядок расположения элементов в той или иной совокупности. Важно лишь то, какие именно элементы ее составляют.

К примеру, представим себе фирму, состоящую из сотрудников. И в предмайские дни необходимо направить несколько () человек на уборку прилегающей территории. Это означает, что из этого – элементного множества необходимо выбрать всевозможные – элементные подмножества. Число таких подмножеств (в нашем случае бригад для уборки территории) равно числу сочетаний из элементов по элементов. В этой выборке порядок неважен (в отличие от размещений). Неважно, кто это будет (Петров, Иванов, Сидоров) или (Сидоров, Петров, Иванов). Главное, что это будут бригады по заданному числу элементов (в нашем случае по определенному количеству человек), попробуем найти это число.

Будем основываться на том, что нам известно: на размещениях и перестановках. Сначала из элементов выделим какие-либо элементов с учетом очередности выбора. Это — размещение, и число таких размещений . Очевидно, что различные размещения, в которые входят те же объекты, но в ином порядке, будут соответствовать одному сочетанию (ведь в сочетании порядок роли не играет). Другими словами, любая перестановка выбранных элементов порождает то же самое сочетание. Но таких перестановок 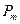. Поэтому число сочетаний из элементов по в 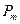раз меньше числа размещений, т. е.

. (1.6)

Если вернуться к теореме о числе размещений, рассмотренной в предыдущей главе, то и число сочетаний можно вычислять следующим образом:

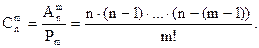(1.7)

Возвращаясь к задаче с фирмой, конкретизируем данные. Пусть 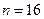, , тогда число всевозможных бригад, которые можно создать для уборки территории в соответствии с равенством 1.8 будет равно:

.

Выходит, что способов создания таких бригад — 560.

Обратите внимание на своеобразную симметрию формулы 1.6: если заменить на 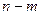, то получится то же самое, только факториалы в знаменателе поменяются местами. Отсюда следует замечательное свойство сочетаний:

. (1.8)

Объясняется это просто: каждому сочетанию из отобранных элементов всегда соответствует сочетание из 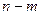оставшихся. Так что можно с самого начала говорить не о выделении объектов из , а о разбиении множества исходных элементов на две части по и по 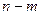в каждой.

Значит, для вычисления 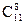по равенству 1.9 достаточно вычислить .

И теперь, если вернуться к задаче о карточке «Лото–миллион», то количество карточек, которые нужно заполнить из 49 номеров по 6, чтобы в них оказались всевозможные комбинации, равно 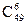. Попытайтесь вычислить это число по формуле 5.6 и с помощью теоремы, т. е. равенства 1.7, оно составит почти 14 миллионов. Можно сделать вывод: для реализации этой задачи уже надо быть миллионером (чтобы приобрести такое количество карточек).

Отметим еще одно свойство сочетаний, которое позволяет рационализировать вычисления. Это свойство запишем без вывода, хотя и доказывается оно очень просто с помощью формулы 1.6.

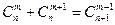. (1.9)

В соответствии с этим свойством и свойством 1.8, вычислим сумму, например такого вида:

.

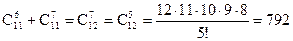Глава 1.5. Сочетания с повторениями

Дата добавления: 2015-06-04