Формальные теории

ОСНОВНЫЕ ПОЛОЖЕНИЯ МАТЕМАТИЧЕСКОЙ ЛОГИКИ

Логика высказывания является одной из разновидностей формальных теорий.

Формальная теория :

1) множество символов ,образующих алфавит;

2) множество слов в алфавите, которые называются формулами;

3) подмножество ; состоит из аксиом;

4) множество отношений 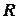(не обязательно бинарных) на множестве формул, которые называются правилами вывода.

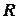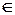
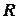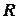Множества и образуют язык, или сигнатуру. Понятия «истинность» и «ложность» отсутствуют. Существенна лишь выводимость, или доказуемость. Пусть – формулы теории . Если существует такое правило вывода , что , то говорят, что формула непосредственно выводима (или доказуема) из формул по правилу вывода (т.е. не является композицией каких-то иных отношений). Обычно этот факт записывают в виде

.

Формулы в числителе называются посылками, а формула в знаменателе – заключением, или секвенцией. Иногда обозначение правила вывода справа от черты дроби опускают, если ясно, о чем идет речь.

Вывод формулы из формул – это такая последовательность формул , что , а любая из формул является либо аксиомой, либо исходной формулой 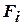, либо непосредственно выводимой из ранее полученных формул.

Если формула выводима из формул в теории , то это обозначается так: . Формулы называются гипотезами вывода. Если формула G непосредственно выводима из аксиом (т.е. без гипотез), то она называется теоремой. Обозначение: .

Если некоторый набор гипотез позволяет вывести формулу, то добавление гипотез не должно приводить к невыводимости:

.

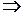
Интерпретацией формальной теории в области интерпретации 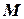называется функция I: 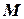, которая с каждой формулой формальной теории сопоставляет некоторое содержательное высказывание относительно объектов множества 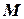. Это высказывание может быть истинным, ложным или не иметь значения истинности. Если соответствующее высказывание является истинным, то формула выполняется в данной интерпретации. Интерпретация называется моделью множества формул, если все формулы этого множества выполняются в данной интерпретации. Интерпретация называется моделью формальной теории, если все теоремы этой теории выполняются в данной интерпретации (т.е. все выводимые формулы модели являются истинными в данной интерпретации).

Формула называется общезначимой (или тавтологией), если она истинна в любой интерпретации.

Дата добавления: 2015-06-04