Исчисление высказываний

Рассмотрим исчисление высказываний как формальную теорию. В алгебре высказываний имеется понятие истинности. В соответствии с общей конструкцией формальных теорий в алгебре высказываний вводятся следующие понятия:

1. Множество символов , образующих алфавит:

– и – связки;

– (, ) – служебные символы;

– – пропозициональные переменные.

2. Формулы:

– переменные суть формулы;

– если 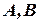– формулы, то ( ) и ( ) – формулы.

3. Аксиомы:

;

;

.

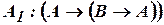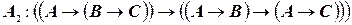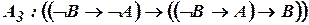Здесь приведены схемы аксиом. Поскольку 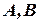и – любые формулы, то аксиом бесконечно много. (В конструктивном определении исчисления высказываний в указанные аксиомы входят конкретные формулы, но вводится еще одно правило вывода.)

4. Правило: – modus ponens.

Другие связки вводятся определениями (а не аксиомами):

.

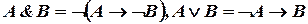Если в формулу подставить вместо переменных 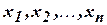подставить соответственно формулы , то получится формула, которая называется частным случаем исходной. Набор подстановок 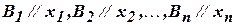называется унификатором. Формула называется совместным частным случаем формул и , если является частным случаем и частным случаем при одном и том же общем унификаторе. Наименьший возможный унификатор называется наиболее общим унификатором.

При конструктивном определении исчисления высказываний помимо приведенного правила modus ponens вводится еще одно, называемое правилом подстановки: если формула является частным случаем формулы , то формула непосредственно выводима из .

Теорема 1. .

Доказательство. В аксиому 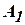: 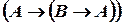вместо подставим .

Тем самым выведем формулу .

По второй аксиоме 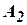: 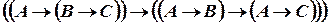. Подставим вместо , вместо :

.

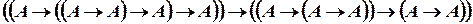Теперь видим, что по правилу modus ponens выводится формула .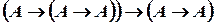

Подключаем 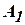: 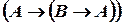, заменив на : .

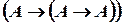По правилу modus ponens , что и требовалось доказать.

Теорема 2. (правило введения импликации).

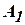Доказательство. – гипотеза. : – гипотеза .

По правилу modus ponens , что и требовалось доказать.

Теорема 3. Если , , то , и наоборот (дедукция).

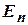
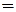
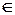
Доказательство. Дано: существуют , такие, что , а – либо аксиомы, либо , либо , либо , .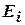

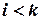Доказательство проводим по индукции. Необходимо доказать, что если существует вывод , то , ,…

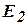1. Докажем, что . Дано: , . Доказать: . Возможны три случая:

а) – аксиома. Применяем первую аксиому: 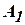: 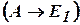. По правилу МР , 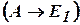МР , или (в левой части аксиомы не пишут);

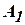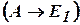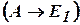б) . Тогда : . Предположим, что . Тогда по МР МР . Значит, , . Но так как , то в левой части писать незачем, и ;

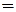
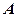
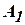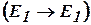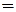
в) . Тогда , . Выше было показано, что . Принимая правую (выведенную) часть , в виде гипотезы и используя : , по правилу МР получаем . Это можно записать в виде . Но , значит, .

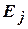
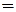
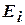
2. Пусть выведены. Выведем : . Возможны те же три случая а – в, которые доказываются аналогично, но существует и четвертый случай: . Используем вторую аксиому :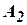

.

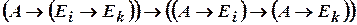Получаем 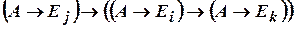. 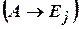– это гипотеза индукции, которая считается выведенной. По МР . Опять-таки, 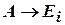– гипотеза вывода, и по МР 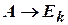. Результат: .

При 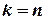приходим к утверждению теоремы.

Обратная теорема: .

Доказательство. Примем выведенное утверждение в качестве гипотезы. Если – гипотеза, то по МР . Отсюда , что и требовалось доказать.

Следствие 1. Если , то , и обратно.

Следствие 2. , 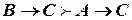(правило транзитивности).

Доказательство. , – гипотезы. По правилу МР , 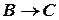– гипотезы. Значит, . Это записываем в виде , , 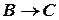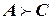. По теореме дедукции , , 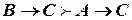что и требовалось доказать.

Следствие 3. , 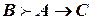(правило сечения).

Другие теоремы:

; ; ;

; ;

; , ….

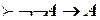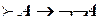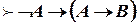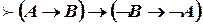Способы доказательства теорем в исчислении высказываний следующие:

1. Использовать методику, приведенную выше. Ее суть – применение аксиом, правил вывода и поиск унификаторов. Каждая выведенная теорема подключается к списку левой части любого вывода. Основное средство – теорема дедукции:

, .

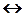
2. С помощью теоремы дедукции привести выводимую в ИВ (исчислении высказываний) формулу к виду теоремы (т.е. от предложенного для вывода перейти к выводу теоремы):

, где .

Далее записать формулу АВ (алгебры высказываний):

.

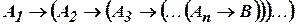Можно также использовать рассмотренные в АВ эквивалентности либо составить таблицу истинности (с помощью ЭВМ) и убедиться в тавтологичности этой формулы (т.е. в том, что при любых значениях пропозициональных переменных она принимает значение «истина»). Если это не так, то формула ИВ не является выводимой.

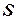
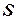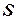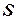
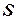
3. В большинстве случаев проще доказывать невыводимость противоположной формулы. Это так называемый метод доказательства от противного: , , где – противоречие, что эквивалентно . Докажем выводимость , если выводимо , . Для этого, как было сказано выше, приведем вывод формулы , к виду теоремы, используя дедукцию:

, .

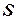
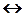
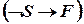
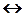
Теперь запишем соответствующую формулу АВ (в булевой форме) и преобразуем, используя эквивалентности АВ:

.

Это значит, что соответствующая формула ИВ выводима: 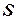. Пользуясь теоремой, обратной к теореме дедукции, приходим к выводу, что 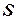, т. е. 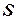выводимо из , что и требовалось доказать.

4. Доказательство от противного лежит в основе метода резолюции, который базируется на выводимости теоремы

.

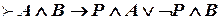Эту теорему нужно доказать. Используем алгебру высказываний (АВ), считая символ «+» дизъюнкцией, а символ «•» конъюнкцией: , что соответствует аналогичной формуле АВ, которую запишем в булевой форме:

.

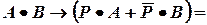
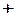
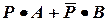Придадим поочередно значения 0 и 1:

;

.

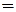
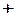
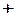
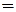
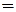
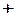
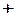
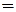
Итак, при любых значениях , , данная формула алгебры высказываний имеет значение «истина», что и означает выводимость теоремы .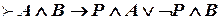

Полученное правило называется правилом резолюции. Пользуясь дедукцией (точнее, обратной теоремой дедукции), это правило можно записать в виде 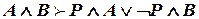, либо в виде правила вывода 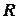метода резолюции:

.

Этим правилом вывода, доказанным вполне строго, можно пользоваться наряду с правилом МР.

Знаменатель правила 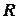имеет название «резольвента».

Дата добавления: 2015-06-04