
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Моделирование релейно-контактных схем
|
|
|
|
Замкнутые классы. Полнота. Теорема Поста
Существует пять классов функций, введенных в рассмотрение Постом:
1. 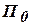 – множество булевых функций, сохраняющих ноль:
– множество булевых функций, сохраняющих ноль:
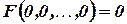 .
.
2. 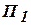 – класс функций, сохраняющих 1:
– класс функций, сохраняющих 1:
 .
.
3.  – класс самодвойственных функций:
– класс самодвойственных функций:
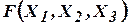 .
.
Двойственная функция 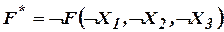 .
.
Функция самодвойственна, если
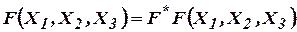 .
.
4.  – класс монотонных функций. Рассмотрим два набора аргументов:
– класс монотонных функций. Рассмотрим два набора аргументов:  ,
,  ,
, 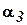 ,
, 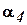 и
и 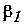 ,
, 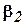 ,
, 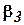 ,
, 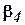 . Предположим, что
. Предположим, что 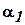

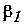 ,
, 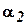

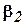 ,
, 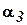

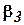 ,
, 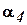
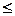
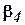 . Если хотя бы один раз выполняется строгое неравенство, то эти наборы сравнимы и первый набор подчинён второму. Функция называется монотонной, если
. Если хотя бы один раз выполняется строгое неравенство, то эти наборы сравнимы и первый набор подчинён второму. Функция называется монотонной, если 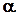
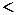
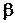
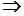


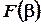 . (Сравнения производить на сравнимых аргументах!)
. (Сравнения производить на сравнимых аргументах!)
5. 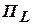 – класс функций, которые представлены в виде
– класс функций, которые представлены в виде
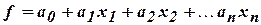 .
.
Все классы замкнуты: если к любому набору функций из некоторого класса применить функцию из того же класса, то результат будет принадлежать к тому же классу.
Таблица свойств некоторых функций:
| 
| 
| 
| 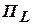
| |
| + | - | - | + | + | |
| - | + | - | + | + | |
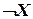
| - | - | + | - | + |
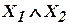
| + | + | - | + | - |
Полнота связана с понятием замыкания. Рассмотрим систему функций. Применим к ней операцию замыкания (для классов Поста эти замыкания совпадают с исходными классами). Предположим, это замыкание совпадает со всем множеством булевых функций (данной размерности). Тогда исходная система функций называется полной.
Теорема Поста. Для того чтобы система функций была полной, необходимо и достаточно, чтобы она включала в себя хотя бы одну функцию, не принадлежащую классу 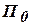 , хотя бы одну функцию, не принадлежащую классу
, хотя бы одну функцию, не принадлежащую классу 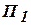 , хотя бы одну функцию, не принадлежащую классу
, хотя бы одну функцию, не принадлежащую классу  , хотя бы одну функцию, не принадлежащую классу
, хотя бы одну функцию, не принадлежащую классу  , хотя бы одну функцию, не принадлежащую классу
, хотя бы одну функцию, не принадлежащую классу 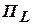 .
.
Пример. Рассмотрим 3-ю и 4-ю строки таблицы. Отрицание и конъюнкция – полная система функций, 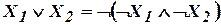 , т. е. дизъюнкцией можно не пользоваться.
, т. е. дизъюнкцией можно не пользоваться.
|
|
|
Контрольное задание
1. Доказать, что отрицание и конъюнкция – полная система.
2. Имеются полные системы, состоящие из одной функции. Доказать, что штрих Шеффера образует полную систему.
3. Доказать, что стрелка Пирса образует полную систему.
4. Выполнить построение СПНФ, использовав варианты, приведенные в подразд. 1.3.
Рассмотрим следующую задачу. Жюри состоит из трех членов А, B, C. Председателем жюри является А. После выполнения упражнения большинством голосов выносится вердикт – «зачтено» или «не зачтено». Учитывается, что в случае, когда B и C голосуют «за», а председатель голосует «против», то предложение «за» отвергается. Перед каждым членом жюри имеется кнопка, при нажатии которой его голос интерпретируется как «за». Лампочка загорается, если принято решение «за». Требуется соединить провода, источник питания, ключи (кнопки) и лампочку для автоматизации процесса голосования.
Для решения задачи предварительно составим логическую функцию, считая ее функцией трех логических переменных  ,
,  ,
,  :
:
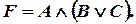
Рассмотрим три простейшие схемы (рис. 1.1 – 1.3), в которых стандартное положение ключа (кнопки) – открытое, при замыкании обеспечивается проводимость участка цепи. Для решения поставленной задачи достаточно несколько усложнить схему (рис. 1.4).

Рис. 1.1. Схема, реализующая «да» и «нет»

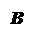
Рис. 1.2. Схема, реализующая конъюнкцию 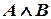
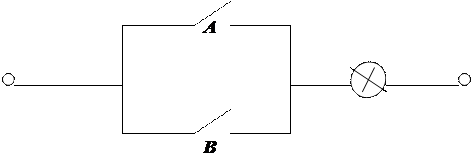 |
Рис. 1.3. Схема, реализующая дизъюнкцию 
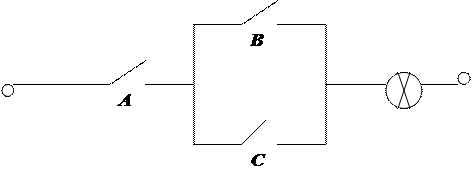 |
Рис. 1.4. Схема, реализующая функцию 
Схема, изображенная на рис. 1.4, и дает решение задачи.
Однако с помощью конъюнкции и дизъюнкции невозможно построить произвольную логическую функцию, поскольку набор функций ( 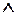 ,
,  ) не образует полного базиса. Его следует дополнить отрицанием. Реализацию отрицания можно, например, получить с помощью так называемого реле, соответствующего каждому ключу. Нажатие кнопки должно замыкать простую цепь, содержащую соленоид. Если стандартное положение ключа открытое, то соленоид своим магнитным полем притягивает подвижную часть ключа до замыкания; если стандартное положение замкнутое, то включение магнитного поля приводит к размыканию, что и реализует функцию «отрицание».
) не образует полного базиса. Его следует дополнить отрицанием. Реализацию отрицания можно, например, получить с помощью так называемого реле, соответствующего каждому ключу. Нажатие кнопки должно замыкать простую цепь, содержащую соленоид. Если стандартное положение ключа открытое, то соленоид своим магнитным полем притягивает подвижную часть ключа до замыкания; если стандартное положение замкнутое, то включение магнитного поля приводит к размыканию, что и реализует функцию «отрицание».
|
|
|
Электрические схемы, содержащие реле, называются релейно-контактными. С их помощью можно технически реализовать любую булеву функцию. Недостатком реле является сравнительно низкое быстродействие. Поэтому исторически роль реле перешла сначала к электронной лампе – триоду, далее к транзисторам, а затем к интегральным схемам с очень большой скоростью замыкания контактов ключей.
Таким образом, логика работы релейно-контактных схем обеспечивается элементами, реализующими операции «И» (конъюнкция), «ИЛИ» (дизъюнкция) и «НЕ» (отрицание). Для построения оптимальной по количеству используемых ключей релейно-контактной схемы следует применить минимизацию. Метод Квайна – Мак-Класки позволяет привести СНДФ к минимальной НДФ. Однако следует иметь в виду, что если отказаться от требования нормальности, то полученную минимальную НДФ в большинстве случаев можно минимизировать далее.
Пример. Дана функция в НДФ: 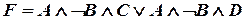 .
.
Эту функцию можно записать в виде матрицы  .
.
Функции соответствует релейно-контактная схема, содержащая два плеча, соединенных параллельно; в одном плече последовательно соединены ключи для реализации A, רB и C, во втором –  ,
, 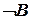 и
и 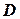 .
.
Дальнейшую минимизацию можно осуществить путем вынесения общего множителя:  .
.
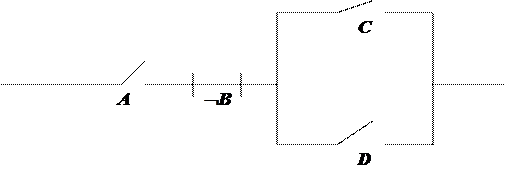 Результат показан на рис. 1.5.
Результат показан на рис. 1.5.
Рис. 1.5. Релейно-контактная схема 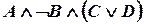
Котрольное задание
Варианты заданий по данной теме приведены в подразд. 1.3.
Требуется выполнить следующее:
– нарисовать релейно-контактную схему, соответствующую заданной СНДФ;
– методом Квайна – Мак-Класки привести СНДФ к виду минимальной НДФ;
– произвести (если это возможно) дальнейшую минимизацию, используя вынесение общих множителей за скобки;
– нарисовать релейно-контактную схему для полученной логической функции.
|
|
|
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 1822; Нарушение авторских прав?; Мы поможем в написании вашей работы!