
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение булевых функций
|
|
|
|
БУЛЕВЫ ФУНКЦИИ
Булевой функцией 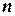 переменных будем называть однозначное отображение пространства
переменных будем называть однозначное отображение пространства 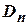 , которое является прямым произведением пространств
, которое является прямым произведением пространств 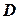 , состоящих из двух элементов, в пространство
, состоящих из двух элементов, в пространство 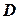 . Один из элементов будем обозначать Ø (или «ложь», «Л», «false»), другой – 1 (или «истина», «И», «true»). Пространство аргументов
. Один из элементов будем обозначать Ø (или «ложь», «Л», «false»), другой – 1 (или «истина», «И», «true»). Пространство аргументов 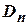 содержит
содержит 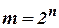 элементов, каждый из которых записывается в виде
элементов, каждый из которых записывается в виде 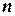 -мерного вектора
-мерного вектора 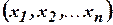 . Общее количество различных булевых функций –
. Общее количество различных булевых функций – 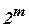 .
.
Среди булевых функций выделяются так называемая тавтология – функция, равная единице при любом наборе аргументов, и противоречие – функция, принимающая значение Ø при любом наборе аргументов. Отрицанием истины считается ложь, и наоборот:  1
1 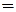 0,
0,  0
0 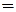 1. Отрицание функции
1. Отрицание функции 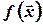 – это такая функция
– это такая функция  , которая для любого набора аргументов принимает значение, противоположное соответствующему значению
, которая для любого набора аргументов принимает значение, противоположное соответствующему значению 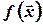 .
.
Таблица истинности – один из способов задания булевой функции. Если для двух функций их значения при каждом наборе аргументов совпадают, то они считаются одной и той же функцией.
В то же время имеется еще одна возможность задания булевых функций с помощью применения специальных обозначений для некоторого класса функций, причем функции, не входящие в этот класс, возникают как суперпозиции функций, входящих в исходный класс. Получаемые выражения называются формулами. Две функции, записываемые с помощью различных формул, являются эквивалентными, если их таблицы истинности совпадают.
Перечень булевых функций двух переменных приведен в табл. 1.1.
Таблица 1.1
Булевы функции
| X 1 | F | Обозначение | Название | ||||
| X 2 | |||||||
| Ø | Противоречие | ||||||
X 1 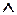 X 2 X 2
| 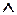 , «.», & , «.», &
| Конъюнкция | |||||
| X 2\ X 1 | \ | Разность | |||||
| X 2 | Проекция Р2 (X1, X2) = X2 | ||||||
| X 1 \ X 2 | Разность | ||||||
| X 1 | Проекция Р1 (X1, X2) = X1 | ||||||
X 1 \ X 2 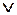
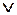 X 1 \ X 2 X 1 \ X 2
| ∆, xor, + | Симметричная разность, сложение по модулю 2 | |||||
X 1 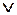 X 2 X 2
| 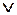 , +, or , +, or
| Дизъюнкция | |||||
 (X 1 (X 1 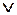 X 2) X 2)
| 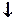
| Стрелка Пирса (польский штрих) | |||||
X 1 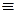 X 2 X 2
| 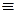 , ,  , , 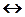
| Эквивалентность | |||||
 X 1 X 1
| 
| Отрицание X1 | |||||
X 1 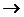 X 2 X 2 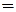
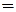  X 1 X 1 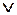 X 2 X 2
| 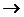
| Импликация | |||||
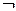 X 2 X 2
| 
| Отрицание X2 | |||||
X 2 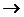 X 1 X 1 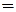
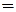  X 2 X 2 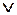 X 1 X 1
| 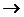
| Импликация | |||||
 (X 1 (X 1 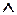 X 2) X 2)
| | Штрих Шеффера | |||||
| I | Тавтология |
Пусть имеется множество 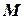 произвольной природы. Предположим, на этом множестве введены операции сложения, умножения и вычитания, подчиняющиеся следующим законам (аксиомам):
произвольной природы. Предположим, на этом множестве введены операции сложения, умножения и вычитания, подчиняющиеся следующим законам (аксиомам):
- коммутативные законы:
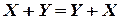 ,
, 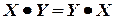 ;
;
- ассоциативные законы:
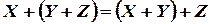 ,
, 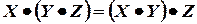 ;
;
- дистрибутивные законы:
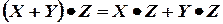 ,
, 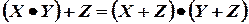 ;
;
- законы идемпотентности:
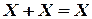 ,
, 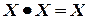 ;
;
- закон двойного отрицания
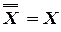 ;
;
- законы Де Моргана:
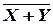
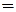
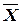
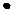
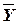 ,
, 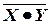
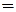
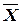
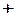
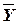 ;
;
- законы поглощения:
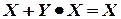 ,
,  .
.
В таком случае данное множество с введенными операциями представляет собой алгебру, притом булеву.
Рассмотренные законы проверяются сопоставлением таблиц истинности для функций в левой и правой частях каждого из приведенных равенств, если использовать перечень функций от двух переменных.
Сопоставим с элементами множества М высказывания, с операциями сложения – дизъюнкцию, с операциями умножения – конъюнкцию, со знаком отрицания – отрицание высказывания, со знаками эквивалентности – равенства. В таком случае обнаружится, что алгебра логики является интерпретацией булевой алгебры. Роль истины играет единица (1), лжи – ноль (0): 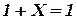 ,
, 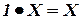 ,
, 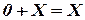 ,
, 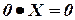 .
.
Еще одна интерпретация булевой алгебры – множества с операциями объединения, пересечения и дополнения. Имеются и другие интерпретации, например релейные схемы.
Исторической заслугой Джорджа Буля является то, что он сконструировал действия алгебры логики, основываясь на некоторой модификации обычных арифметических операций.
С отрицанием величины 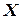 он сопоставил арифметическую разность
он сопоставил арифметическую разность 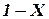 , с конъюнкцией – арифметическое выражение
, с конъюнкцией – арифметическое выражение 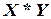 , а с дизъюнкцией – арифметическое выражение
, а с дизъюнкцией – арифметическое выражение 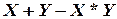 . Данные операции даже использовались как эквиваленты логических операций в первых ЭВМ.
. Данные операции даже использовались как эквиваленты логических операций в первых ЭВМ.
Пользуясь приведенными выше аксиомами, формулы, с помощью которых задается булева функция, можно привести к эквивалентным формулам в целях максимального их упрощения.
Контрольные задания
1. Максимально упростить выражение своего варианта, воспользовавшись законами логики Буля. Затем с помощью таблиц истинности сравнить упрощенное выражение с исходным:
1) (a  (רd
(רd  b))
b))  ((רa
((רa  (רb
(רb  d))
d))  c)
c)  רc
רc  (a
(a  (b
(b  רd)),
רd)),
2) ((a  c)
c)  (a
(a  d))
d))  (((c
(((c  (c
(c  b))
b))  רc)
רc)  רa),
רa),
3) (רb  d)
d)  ((רd
((רd  c)
c)  (a
(a  c)
c)  (רd
(רd  רc)
רc)  (a
(a  רc))
רc))  (b
(b  d),
d),
4) (a  רc)
רc)  (רa
(רa  רb)
רb)  (רb
(רb  c)
c)  (רa
(רa  b)
b)  (b
(b  c),
c),
5) (a  c)
c)  ((b
((b  רd)
רd)  (רa
(רa  רd)
רd)  (d
(d  b)
b)  (רa
(רa  d))
d))  (a
(a  רc),
רc),
6) ((רb  רc)
רc)  (a
(a  b))
b))  (d
(d  רc)
רc)  (((רb
(((רb  רa)
רa)  c)
c)  (a
(a  b)),
b)),
7) (a  רc)
רc)  (רa
(רa  רb)
רb)  (b
(b  c)
c)  (רa
(רa  b)
b)  (c
(c  רb),
רb),
8) ((a  (c
(c  (b
(b  c)))
c)))  ר(c
ר(c  d)
d)  (c
(c  רd))
רd))  (c
(c  (רd
(רd  רc)
רc)  d),
d),
9) ((a  רa)
רa)  (רb
(רb  רd)
רd)  (רb
(רb  רc)
רc)  (רc
(רc  d))
d))  ((רb
((רb  c)
c)  (c
(c  d)),
d)),
10) (a  רc)
רc)  ((רa
((רa  d)
d)  (b
(b  d)
d)  (רa
(רa  רd)
רd)  (b
(b  רd))
רd))  (a
(a  c),
c),
11) ((d  רc)
רc)  (רd
(רd  רb)
רb)  (c
(c  רb))
רb))  ((רd
((רd  b)
b)  (c
(c  b))
b))  (רa
(רa  a),
a),
12) ((רc  רd)
רd)  (b
(b  c))
c))  (רa
(רa  רd)
רd)  (((רc
(((רc  רb)
רb)  d)
d)  (c
(c  b)),
b)),
13) ((a  b)
b)  (רb
(רb  c
c  d)
d)  (רa
(רa  רb
רb  c
c  d)
d)  רb
רb  רc
רc  d,
d,
14) ((a  b)
b)  (a
(a  רb))
רb))  ((רa
((רa  b)
b)  (c
(c  רd)
רd)  (רa
(רa  רb)
רb)  (d
(d  c)),
c)),
15) ((רb  c)
c)  (רc
(רc  d)
d)  רa)
רa)  (רa
(רa  b
b  רc
רc  d)
d)  ר(c
ר(c  d)
d)  a,
a,
16) ((b  c)
c)  (d
(d  (רb
(רb  רc)))
רc)))  (רd
(רd  רa)
רa)  ((c
((c  b)
b)  (רd
(רd  רc)),
רc)),
17) (b  d)
d)  ((c
((c  רd)
רd)  (a
(a  c)
c)  (רd
(רd  רc)
רc)  (a
(a  רc))
רc))  (רb
(רb  d),
d),
18) ((רc  d)
d)  (d
(d  a))
a))  ((b
((b  רb)
רb)  (רc
(רc  רa)
רa)  (רc
(רc  רd)
רd)  (רd
(רd  a)),
a)),
19) (a  רd)
רd)  (((רc
(((רc  רb)
רb)  d)
d)  (c
(c  b))
b))  ((רd
((רd  רc)
רc)  (c
(c  b)),
b)),
20) (((d  (d
(d  c))
c))  רd)
רd)  רb)
רb)  ((b
((b  d)
d)  (b
(b  a)),
a)),
21) ((רb  (רc
(רc  a))
a))  d))
d))  רd
רd  (b
(b  (c
(c  רa))
רa))  (b
(b  (רa
(רa  c)),
c)),
22) ((c  רa)
רa)  (רa
(רa  רb)
רb)  (a
(a  c)
c)  (רb
(רb  a))
a))  (b
(b  רd)
רd)  (b
(b  d),
d),
23) (d  (רa
(רa  רd)
רd)  a)
a)  ((b
((b  (d
(d  (d
(d  c)))
c)))  ר(c
ר(c  a)
a)  (d
(d  רa)),
רa)),
24) (רc  רb)
רb)  (d
(d  c)
c)  (רb
(רb  с)
с)  (d
(d  רc)
רc)  (b
(b  רd).
רd).
Пример. (רc  רb)
רb)  (d
(d  c)
c)  (רb
(רb  c)
c)  (d
(d  רc)
רc)  (b
(b  רd):
רd):
1) (רc  רb)
רb)  (רb
(רb  c)= רb,
c)= רb,
2) (d  c)
c)  (d
(d  רc)= d,
רc)= d,
3) d  (b
(b  רd)= (b
רd)= (b  d)
d)  (d
(d  רd)= (b
רd)= (b  d)
d)  I= b
I= b  d,
d,
4) רb  d
d  (b
(b  רd)= רb
רd)= רb  b
b  d=I
d=I  d=I.
d=I.
2. Установить эквивалентность левой и правой частей следующих логических выражений:
1) ((a|b)|(a~b))|((c+d)→(d/c))=((b→c)→(a/c))↓((a|d)|(d→ רb)),
2) ((a  רc)↓(b/c))
רc)↓(b/c))  ((a|d)/(b
((a|d)/(b  d))=((a|b)|(a+ רb))→((c+d)
d))=((a|b)|(a+ רb))→((c+d)  (d→c)),
(d→c)),
3) ((a↓b)  (a+b))/((c/d)↓(c~d))=((c→a)
(a+b))/((c/d)↓(c~d))=((c→a)  (c→b)) →((a↓d)
(c→b)) →((a↓d)  (b↓d)),
(b↓d)),
4) ((a~b)/(a↓b))↓((c~d)↓(c/d))=((c/a)↓(c/b))|((a↓d)↓(b↓d)),
5) ((a  b)
b)  (a+b))/((d/c)↓(d~c))=((a→c)
(a+b))/((d/c)↓(d~c))=((a→c)  (b→c)) →((a|d)|(b|d)),
(b→c)) →((a|d)|(b|d)),
6) ((a  b)/(a+b))
b)/(a+b))  ((c/d)↓(c~d))=((c/a)↓(c/b))
((c/d)↓(c~d))=((c/a)↓(c/b))  ((a
((a  d)/(b↓d)),
d)/(b↓d)),
7) ((d→b)→(רc/b))↓((c  a)|(d→a))=((רc|d)|(c+d))|((a~b)→(רa/b)),
a)|(d→a))=((רc|d)|(c+d))|((a~b)→(רa/b)),
8) ((a|b)/(רa+ רb))  ((d/c)↓(c~d))=((רa↓ רd)↓(b/ רd))
((d/c)↓(c~d))=((רa↓ רd)↓(b/ רd))  ((a→c)/(b/c)),
((a→c)/(b/c)),
9) ((c/a)  (c~a))/((d/b)↓(d~b))=((a
(c~a))/((d/b)↓(d~b))=((a  b)
b)  (c→b))→((d/a)
(c→b))→((d/a)  (c
(c  d)),
d)),
10) ((c~b)/(b↓c))↓((רa~ רd)↓(a/d))=((b↓d)↓(c↓d))|((a/b)↓(a/c)),
11) ((a/d)  (a~d))/((b/c)↓(b~c))=((b→d)
(a~d))/((b/c)↓(b~c))=((b→d)  (a|b))→((c
(a|b))→((c  d)|(a→c)),
d)|(a→c)),
12) ((b↓d)↓(c↓d))  ((a→b)/(a/c))=((b
((a→b)/(a/c))=((b  c)/(b+c))
c)/(b+c))  ((a/d)↓(a~d)),
((a/d)↓(a~d)),
13) ((c→d)|(c+d))|((a~b)→(a  b))=((a→ רc)→(a/d))↓((b→d)|(b→ רc)),
b))=((a→ רc)→(a/d))↓((b→d)|(b→ רc)),
14) ((b  d)↓(b
d)↓(b  c))
c))  ((d→a)/(c/a))=((c|d)|(רc~ רd))→((a+b)
((d→a)/(c/a))=((c|d)|(רc~ רd))→((a+b)  (b→a)),
(b→a)),
15) ((d/a)  (d~a))/((c/b)↓(רc+b))=((a
(d~a))/((c/b)↓(רc+b))=((a  b)
b)  (d→b))→((c
(d→b))→((c  d)
d)  (c/a)),
(c/a)),
16) ((c→d)/(c~d))  ((a
((a  b)↓(a+b))=((b
b)↓(a+b))=((b  c)↓(b/d))
c)↓(b/d))  ((a|c)/(a/d)),
((a|c)/(a/d)),
17) ((רc→b)→(d↓b))↓((a→d)|(a→c))=((c  d)|(c~d))|((רa+ רb)→(a/b)),
d)|(c~d))|((רa+ רb)→(a/b)),
18) ((a  c)↓(b/ רa))
c)↓(b/ רa))  ((c→d)/(b/d))=((b|c)|(b~c))→((a+d)
((c→d)/(b/d))=((b|c)|(b~c))→((a+d)  (a→d)),
(a→d)),
19) ((b↓ רd)  (רb+d))/((a/c)↓(a~c))=((רc→b)
(רb+d))/((a/c)↓(a~c))=((רc→b)  (d→c)) →((a/b)
(d→c)) →((a/b)  (a
(a  d)),
d)),
20) ((d  a)↓(b
a)↓(b  d))|((a/c)↓(b/c))=((a+ רb)/(b
d))|((a/c)↓(b/c))=((a+ רb)/(b  a))↓((רc~ רd)↓(d/c)),
a))↓((רc~ רd)↓(d/c)),
21) ((a↓b)  (רa~b))/((c/d)↓(c~d))=((רa→d)
(רa~b))/((c/d)↓(c~d))=((רa→d)  (רd→b))→((c→a)|(c→b)),
(רd→b))→((c→a)|(c→b)),
22) ((c→a)/(a+ רc))  ((d/b)↓(b~d))=((a↓b)↓(c/b))
((d/b)↓(b~d))=((a↓b)↓(c/b))  ((d→a)/(c
((d→a)/(c  d)),
d)),
23) ((c| רb)|(c~ רb))|((רa+ רd)→(רa/ רd))=((c→ רd)→(רb/ רd))↓
↓((רb| רa)|(רa→c)),
24) ((c↓ רb)  (c+ רb))/((רd/ רa)↓(רd~ רa))=((רd→ רb)
(c+ רb))/((רd/ רa)↓(רd~ רa))=((רd→ רb)  (רd→c))→
(רd→c))→
→ ((רb↓ רa)  (c↓ רa)).
(c↓ רa)).
Пример основных фрагментов программы:
/ frazn, + xor,  or,
or,  and,
and, 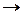 fimp,
fimp, 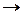 fsp,
fsp,
| fsh, ~, = feqv – логические функции и их идентификаторы;
function fsp(x,y:boolean): boolean;
begin fsp:=(not x) and (not y); end;
function feqv(x,y:boolean): boolean;
begin feqv:=(not x) and (not y) or x and y; end;
function frazn(x,y:boolean): boolean;
begin frazn:=x and (not y); end;
function fimp(x,y:boolean): boolean;
begin fimp:=(not x) or y; end;
begin
for a:=false to true do
for b:=false to true do
for c:=false to true do
for d:=false to true do begin
m1:=fsp(c,not b); m2:=c xor (not b); m3:=frazn(not d,not a); m4:=feqv(not d,not a); m5:=m1 or m2; m6:=fsp(m3,m4);
f1:=frazn(m5,m6);
n1:=fimp(not d,not b); n2:=fimp(not d,c); n3:=fsp(not b,not a);
n4:=fsp(c,not a); n5:=n1 and n2; n6:=n3 or n4;
f2:=fimp(n5,n6);
fsrav:=feqv(f1,f2);
write('| ');
if a then write('1') else write('0');
if b then write(' 1') else write(' 0');
if c then write(' 1') else write(' 0');
if d then write(' 1') else write(' 0');
write(' | ');
if f1 then write(' 1') else write(' 0');
write(' | ');
if f2 then write(' 1') else write(' 0');
write(' | ');
if fsrav then write(' 1') else write(' 0');
writeln(' | ');
end;
readln;
end.
Результат работы программы – таблица истинности:

|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 668; Нарушение авторских прав?; Мы поможем в написании вашей работы!