Вопрос 14. Процентные ставки и методы их начисления

Оценка стоимости денег с учетом фактора времени связана с со следующими базовыми понятиями:

Процент – сумма дохода от предоставления капитала в долг или плата за пользование ссудным капиталом во всех его формах (депозитный процент, кредитный процент, процент по облигациям, процент по векселям и т.п.).

Простой процент – сумма дохода, начисляемого к основной сумме капитала в каждом интервале, по которым дальнейшие расчеты платежей не осуществляются. Начисление простого процента применяется, как правило, при краткосрочных финансовых операциях.

Сложный процент – сумма дохода, начисляемого в каждом интервале, которая не выплачивается, а присоединяется к основной сумме капитала и в последующем платежном периоде сама приносит доход. Начисление сложного процента применяется, как правило, при долгосрочных финансовых операциях.

Процентная ставка – ставка, которая характеризует соотношение суммы процента и суммы предоставленного (заимствованного) капитала (выраженное в десятичной дроби или в процентах).

Будущая стоимость денег – наращенная сумма будущих денежных средств сумма с учетом определенной процентной ставки за счет инвестирования в настоящий период времени.

Настоящая стоимость денег – сумма будущих денежных средств, приведенных с учетом определенной процентной ставки к настоящему периоду времени.

Наращиванье стоимости (компаундинг) – процесс приведения настоящей стоимости денег к их будущей стоимости в определенном периоде путем присоединения к их первоначальной сумме начисленной суммы процентов.

Дисконтирование стоимости (дисконтирование) – процесс приведения будущей стоимости капитала (денежных средств) к их настоящей стоимости путем изъятия из их будущей суммы соответствующей суммы процентов.

Дисконт (скидка) – эторазница между первоначальной и конечной ценой (стоимостью) капитала.

Период начисления – общий период времени, в течение которого осуществляется процесс наращения или дисконтирования стоимости денежных средств.

В практике финансовых вычислений используются следующие методики:

1. Методический инструментарий оценки стоимости денег по простым процентам:

- При расчете суммы простого процента в процессе наращения стоимости (компаундинга);

- При расчете суммы простого процента в процессе дисконтирования стоимости (т.е. суммы дисконта).

1.1. При расчете суммы простого процента в процессе наращения стоимости (компаундинга) используется следующая формула:

I = P × n × i, (1)

где I – сумма процента за обусловленный период времени в целом;

Р – первоначальная сумма (стоимость) денежных средств;

n – количество интервалов расчета процентных платежей, в общем, периоде времени;

i – используемая процентная ставка, выраженная десятичной дробью.

В этом случае будущая стоимость вклада (S) с учетом начисленной суммы процента определяется по формуле:

S = P + I; I = (1 + ni), (2)

где S – будущая стоимость вклада;

P – первоначальная сумма (стоимость) денежных средств;

I – сумма процента за обусловленный период времени в целом;

(1 + ni) – множитель (или коэффициент) наращения суммы простых процентов. Его значение всегда должно быть больше единицы.

1.2. При расчете суммы простого процента в процессе дисконтирования стоимости (т.е. суммы дисконта) используется следующая формула:

, (3)

где D – сумма дисконта (рассчитанная по простым процентам) за период времени в целом;

S – стоимость денежных средств;

n – количество интервалов, по которым осуществляется расчет процентных платежей, в общем периоде времени;

i – используемая дисконтная ставка, выраженная десятичной дробью.

В этом случае настоящая стоимость денежных средств (Р) с учетом рассчитанной суммы дисконта определяется по следующим формулам:

, (4)

где Р – настоящая стоимость денежных средств;

D – сумма дисконта (рассчитанная по простым процентам) за период времени в целом;

S – стоимость денежных средств;

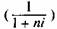– множитель (коэффициент) простых процентов, значение которого всегда должно быть меньше единицы.

2. Методический инструментарий оценки стоимости денег по сложным процентам:

- При расчете будущей суммы вклада (стоимости денежных средств) в процессе его наращения по сложным процентам;

- При расчете настоящей стоимости денежных средств в процессе дисконтирования по сложным процентам;

- При определении средней процентной ставки, используемой в расчетах стоимости денежных средств по сложным процентам;

- Длительность общего периода платежей, выраженная количеством его интервалов в расчетах стоимости денежных средств по сложным процентам;

- Определение эффективной процентной ставки в процессе наращения стоимости денежных средств по сложным процентам.

2.1. При расчете будущей суммы вклада (стоимости денежных средств) в процессе его наращения по сложным процентам используется следующая формула:

S_c = P × (1+i)ⁿ , (5)

где S_c – будущая стоимость вклада (денежных средств) при его наращении по сложным процентам;

P – первоначальная сумма вклада;

i – используемая процентная ставка, выраженная десятичной дробью;

n – количество интервалов, по которым осуществляется каждый процентный платеж, в общем обусловленном периоде времени.

Соответственно сумма процента (I_с) в этом случае определяется по формуле:

I_c = S_c – P, (6)

где I_с – сумма процента;

S_c – будущая стоимость вклада (денежных средств) при его наращении по сложным процентам;

P – первоначальная сумма вклада.

2.2. При расчете настоящей стоимости денежных средств в процессе дисконтирования по сложным процентам используется следующая формула:

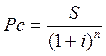, (7)

где P_C – первоначальная сумма вклада;

S – будущая стоимость вклада при его наращении, обусловленная условиями инвестирования;

i – используемая дисконтная ставка, выраженная десятичной дробью;

n – количество интервалов, по которым осуществляется каждый процентный платеж, в общем обусловленном периоде времени.

Соответственно сумма дисконта (D_с) в этом случае определяется по формуле:

D_c =S - P_c, (8)

где D_с – сумма дисконта;

P_C – первоначальная сумма вклада;

S – будущая стоимость вклада при его наращении, обусловленная условиями инвестирования.

2.3. При определении средней процентной ставки, используемой в расчетах стоимости денежных средств по сложным процентам, применяется следующая формула:

, (9)

где i – средняя процентная ставка, используемая в расчетах стоимости денежных средств по сложным процентам, выраженная десятичной дробью;

S_c – будущая стоимость денежных средств;

P_c – настоящая стоимость денежных средств;

n – количество интервалов, по которым осуществляется каждый процентный платеж, в общем обусловленном периоде времени.

2.4. Длительность общего периода платежей, выраженная количеством его интервалов в расчетах стоимости денежных средств по сложным процентам определяется путем логарифмирования по следующей формуле:

, (10)

где n – длительность общего периода платежей;

Sc – будущая стоимость денежных средств;

P_c – настоящая стоимость денежных средств;

i – используемая процентная ставка, выраженная десятичной дробью.

2.5. Определение эффективной процентной ставки в процессе наращения стоимости денежных средств по сложным процентам осуществляется по формуле:

, (11)

где i_э – эффективная среднегодовая процентная ставка при наращении стоимости денежных средств по сложным процентам, выраженная десятичной дробью;

i – периодическая процентная ставка, используемая при наращении стоимости денежных средств по сложным процентам, выраженная десятичной дробью;

n – количество интервалов, по которым осуществляется каждый процентный платеж по периодической процентной ставке на протяжении года.

При оценке стоимости денег во времени по сложным процентам необходимо иметь в виду, что на результат оценки оказывает большое влияние не только используемая ставка процента, но и число интервалов выплат в течение одного и того же общего платежного периода. Иногда оказывается более выгодным инвестировать деньги под меньшую ставку процента, но с большим числом интервалов в течение предусмотренного периода платежа.

Используемые в процессе оценки стоимости денег множители:

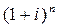– множитель наращения суммы сложных процентов;

– множитель дисконтирования суммы сложных процентов.

Дата добавления: 2015-06-04