Как меняются амплитуды вдоль прямой

Квантованные уровни энергии

Уравнение Шредингера

Нормировка состояний с определенной координатой х

Состояния с определенным импульсом

Волновая функция

Как меняются амплитуды вдоль прямой

ЗАВИСИМОСТЬ АМПЛИТУД ОТ МЕСТА

Главa 14

Основное состояние здесь на самом деле «вырождено». Существуют и другие состояния с той же энергией, например, когда все спины смотрят вниз или в любую другую сторону. Но наложение самого слабого внешнего поля в направлении z снабдит все эти состояния различной энергией, и истинным основным состоянием окажется как раз то, которое мы выбрали.

Выясним теперь, как в квантовой механике амплитуды вероятности меняются в простран­стве. В некоторых предыдущих главах у вас могло возникнуть смутное чувство, что кое о чем мы умалчиваем. Например, когда мы тол­ковали о молекуле аммиака, мы решили описы­вать ее через два базисных состояния. За одно из них мы выбрали случай, когда атом азота находится «выше» плоскости трех атомов во­дорода, а в качестве другого базисного состояния выбрали такие условия, когда атом азота стоит «ниже» плоскости трех атомов водорода. Почему же мы выбрали именно эту пару состоя­ний? Почему бы не считать, что атом азота мо­жет оказаться либо на расстоянии 2Å от плос­кости трех атомов водорода, либо на расстоянии 3Å, а может, и 4Å. Ведь атом азота может зани­мать множество положений. Или, когда шла речь о молекулярном ионе водорода, в котором имеется электрон, распределенный между двумя протонами, мы тоже вообразили два базисных состояния. Одно — когда электрон находится по соседству с протоном № 1, и другое, когда он пребывает в окрестностях протона № 2. Ясно, что многие детали мы упустили. Электрон ведь находится не точно у самого протона № 2, а только в его окрестностях. Он может оказаться и где-то повыше протона, и где-то пониже, и где-то слева, и где-то справа.

Мы намеренно избегали уточнения таких деталей. Мы говорили, что нас интересуют только определенные стороны проблемы, и вооб­ражали, что если уж электрон находится по­близости от протона № 1, то он принимает некоторое довольно определенное положение.

На самом деле в этих условиях вероятность обнаружить элект­рон обладает каким-то определенным распределением в про­странстве вблизи протона. Но нас такие детали не заботили. Можно представить дело и иначе. Когда мы рассматривали молекулярный ион водорода, то избрали приближенный под­ход, описывая положение вещей на языке двух базисных со­стояний. В действительности же таких состояний уйма. Электрон может попасть вблизи протона в свое наинизшее, или основное, состояние, но имеется еще и множество возбужденных состояний. В каждом из них электрон как-то по-особому распре­делен вблизи протона. Эти возбужденные состояния мы игно­рировали, говоря, что нас интересуют лишь условия при наи­низшей энергии. Но как раз они-то, эти возбужденные состоя­ния, и приводят к тому, что возможны различные распределе­ния электрона вокруг протона. Если мы хотим детально описать молекулярный ион водорода, то следует принять во внимание и эти прочие допустимые базисные состояния. Это можно сделать многими способами, и один из них — детальнее рассмотреть состояния, когда расположение электрона в пространстве опи­сывается более тщательно.

Мы уже достаточно подготовлены, чтобы заняться более трудоемкой процедурой, которая позволит нам обстоятельнее го­ворить о местоположении электрона, задавая амплитуду вероят­ности того, что он будет обнаружен в каком угодно месте в данной ситуации. Эта более полная теория позволит подкре­пить те приближения, которыми мы раньше пользовались. Наши прежние уравнения в каком-то смысле смогут быть вы­ведены как своего рода приближения к более полной теории. Вас может удивить, почему мы не начали прямо с более полной теории и не делали приближений по мере движения вперед. Но мы считали, что, отправившись от приближения двух состояний и постепенно подходя к более полной теории, вам будет легче достичь понимания всей механики квантовой ме­ханики. Наш подход, по-видимому, противоположен тому, ко­торый вы найдете во многих книгах.

Когда мы обратимся к теме этой главы, вы заметите, что мы нарушаем правило, которому в прошлом неизменно следовали. Какой бы темы мы ни касались, мы всегда пытались более или менее полно представить вам физику дела, указывая как можно полнее, куда ведут эти идеи. Мы стремились наряду с описанием общих следствий теории представить и некоторые характерные детали, чтобы вам было ясно, куда ведет эта теория. А теперь нам придется нарушить это правило. Мы расскажем об ампли­тудах вероятности пребывания электрона где-то в пространстве и продемонстрируем вам дифференциальные уравнения, которым они удовлетворяют. Но у нас не будет времени углубиться и обсудить многие очевидные выводы, следующие из теории.

Более того, нам даже не удастся связать эту теорию с некоторы­ми приближенными формулировками, к которым мы раньше прибегали, скажем, когда изучали молекулу водорода или молекулу аммиака. На этот раз придется бросить дело на пол­пути, не окончив его. Курс наш близится к концу, и хочешь не хочешь, придется обойтись одним только введением в общие представления. Мы укажем связь с тем, о чем говорилось рань­ше, и, кроме того, некоторые другие подходы к задачам кванто­вой механики. Надеемся, что этих представлений вам хватит, чтобы потом двинуться самостоятельно и уже по книгам узнать многие выводы из приведенных здесь уравнений. Все-таки нужно оставить кое-что и на будущее.

Вспомним еще раз, что нам известно о том, как электрон может продвигаться вдоль линии атомов. Когда электрон может с какой-то амплитудой перепрыгивать от одного атома к сосед­нему, то имеются состояния определенной энергии, в которых амплитуда вероятности обнаружить электрон распределяется вдоль решетки в виде бегущей волны. Для длинных волн (малых значений волнового числа К) энергия состояния пропорциональ­на квадрату волнового числа. Для кристаллической решетки с постоянной b, в которой амплитуда того, что электрон в еди­ницу времени перепрыгнет от одного атома к следующему, равна iA/h, энергия состояния связана с k (при малых kb) фор­мулой

E=Ak²b² (14.1)

(см. гл. 11, § 1). Мы видели также, что группы таких волн с близкими энергиями образуют волновой пакет, который ведет себя как классическая частица с массой m_эфф:

Раз волны амплитуды вероятности в кристалле ведут себя как частицы, то естественно ожидать, что общее квантовомеханическое описание частицы выявит такое же волновое поведение, какое мы наблюдали в решетке. Предположим, мы взяли одно­мерную решетку и вообразили, что постоянная решетки b стано­вится все меньше и меньше. В пределе получилось бы, что элект­рон может оказаться в любой точке линии. Нам пришлось бы перейти к непрерывному распределению амплитуд вероятности. У электрона появилась бы амплитуда оказаться в любом месте линии. Таков был бы один из путей описания движения электро­нов в вакууме. Иными словами, если мы вообразим, что все пространство можно пронумеровать бесконечным числом очень тесно расположенных точек, и сможем вывести уравнения, связывающие между собой амплитуды в одной точке с амплитудами в соседних, то получим квантовомеханические законы движения электрона в пространстве.

Начнем с того, что напомним некоторые общие принципы квантовой механики. Пусть имеется частица, которая может в квантовомеханической системе существовать в разных усло­виях. Любые заданные условия, в которых может быть обна­ружен электрон, мы называем «состоянием» и отмечаем их при помощи вектора состояния, скажем |j>. В каких-то других условиях и метка будет другая, скажем вектор состояния |y>. Затем мы вводим идею о базисных состояниях. Мы говорим, что имеется совокупность состояний | 1 >, | 2>, | 3>, | 4> и т. д., обладающая следующими свойствами. Во-первых, все эти со­стояния совершенно различны — мы говорим, что они ортого­нальны. Под этим мы понимаем, что для любой пары базисных состояний | i > и | j > равна нулю амплитуда < i | j > того, что электрон, будучи в состоянии | j >, окажется также и в состоя­нии < i |, если только, конечно, | i > и | j > не обозначают одного и того же состояния. Все это символически представляется

так:

< i | j >=d _ij (14.3)

Вспомните, что d_ij=0, если i и j различны, и d _ij =1, если i и j одинаковые числа.

Далее, базисные состояния | i >обязаны быть полной сово­купностью, так чтобы любое состояние могло быть выражено на их языке. Иначе говоря, любое состояние |j> может быть полностью описано заданием всех амплитуд < i |j> того, что частица в состоянии |j> обнаружится также в состоянии | i >. Вектор состояния |j> представляется суммой базисных со­стояний, умноженных каждое на коэффициент, являющийся амплитудой того, что состояние |j> находится также в состоя­нии | i >:

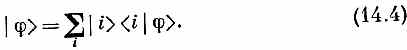
Наконец, если рассмотреть любые два состояния |j> и |y>, то амплитуду того, что состояние |y>окажется также в состоянии |j>, можно найти, проецируя сперва состояние |y> на базисные состояния, а затем каждое из базисных со­стояний — на состояние |j>. Это записывается так:

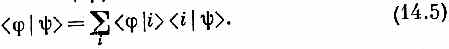
Суммирование, конечно, проводится по всей совокупности ба­зисных состояний | i >.

В гл. 11,когда мы рассчитывали, что бывает с электроном, помещенным в линейную цепочку атомов, вы выбрали совокуп­ность базисных состояний, в которых электрон был расположен близ того или иного из атомов цепочки. Базисное состояние | n > представляло электрон, локализованный (расположенный) возле атома номер п. (Конечно, неважно, обозначать ли наши базисные состояния | n > или | i >.) Чуть позже мы нашли, что базисные состояния удобнее метить координатой атома, а не номером атома в цепочке. Состояние | х_n > — это просто другой способ записи состояния | n >. Тогда, следуя общему правилу, любое состояние |y> можно описать заданием того, что электрон в состоянии |y> находится также в одном из состояний | х_n >. Для удобства мы решили обозначать эти амплитуды символом

C_n= < x_n |y>. (14.6)

Поскольку базисные состояния связаны с местоположением электрона на линии, то амплитуду С_n можно рассматривать как функцию координаты х и писать ее в виде С (х_n). Амплитуды С (х_n)будут в общем случае меняться во времени и поэтому суть также функции от t, но мы не будем отмечать эту зависи­мость явно.

Кроме того, в гл. 11 мы предположили, что амплитуды С(х_n) обязаны меняться во времени так, как положено по гамильтонову уравнению (11.3). В нашем новом обозначении это уравне­ние имеет вид

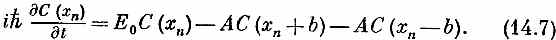
Два последних слагаемых в правой части представляют такой процесс, когда электрон, находившийся возле атома (n +1) или возле атома (n- 1), окажется возле атома (n).

Мы нашли, что (14.7) имеет решения, отвечающие состоя­ниям определенной энергии. Мы записывали их в виде

У состояний с низкой энергией длины волн велики (k мало) и энергия связана с k формулой

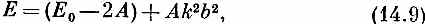
или, если выбрать нуль энергии так, чтобы было (Е₀- 2 А)= 0, то энергия дается формулой (14.1).

Посмотрим, что бы произошло, если бы мы позволили рас­стоянию b между атомами решетки стремиться к нулю, сохра­няя волновое число постоянным. Если бы больше ничего не случилось, то последнее слагаемое в (14.9) обратилось бы просто в нуль, и никакой физики бы не осталось. Но предположим, что А и b вместе изменяются так, что при стремлении b к нулю произведение Ab² поддерживается постоянным: с помощью (14.2) мы запишем Аb² в виде постоянной h² /2m_эфф. При этом (14.9) не изменится, но что произойдет с дифференциальным уравнением (14.7)?

Перепишем сперва (14.7) так:

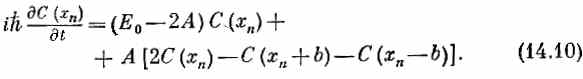
При нашем выборе Е ₀первое слагаемое выпадет. Далее, пред­ставим себе непрерывную функцию С (х), которая плавно про­ходит через значения С (х_n)в точках х_n. Когда расстояние b стремится к нулю, точки х_n сближаются все теснее и теснее и [если С (х)меняется достаточно плавно] величина в скобках попросту пропорциональна второй производной С (х). Можно написать (в чем легко убедиться, разложив в ряд Тэйлора каждый член) равенство

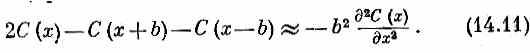
Тогда в пределе, когда b стремится к нулю, а b²A поддерживает­ся равным h2 /2m_эфф, уравнение (14.7) переходит в

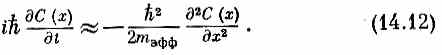
Перед нами уравнение, утверждающее, что скорость изменения С (х) — амплитуды того, что электрон будет обнаружен в х— зависит от амплитуды того, что электрон будет обнаружен в близлежащих точках так, что эта скорость пропорциональна второй производной амплитуды по координате.

Правильное квантовомеханическое уравнение движения электрона в пустом пространстве впервые было открыто Шре­дингером. При движении по прямой оно имеет вид (14.12); надо только m _эфф заменить на m — массу электрона в пустом про­странстве. При движении по прямой в пустом пространстве уравнение Шредингера имеет вид

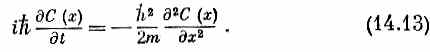
Мы не хотим, чтобы вы считали, будто мы сейчас вывели уравнение Шредингера; мы только показываем вам один из способов, каким его можно осмыслить. Когда Шредингер впер­вые написал его, он привел какой-то вывод, опиравшийся на эвристические доводы и блестящие интуитивные догадки. Не­которые из его доводов были даже неверны, но это не имело значения; важно то, что окончательное уравнение дает правиль­ное описание природы. И цель нашего обсуждения состоит просто в том, чтобы показать вам, что правильное фундаментальное квантовомеханическое уравнение (14.13) имеет ту же самую форму, какая получается в предельном случае электрона, дви­жущегося вдоль цепочки атомов. Это значит, что можно считать, что дифференциальное уравнение (14.13) описывает диффузию амплитуды вероятности от точки к точке вдоль прямой. Иначе говоря, если электрон имеет некоторую амплитуду того, что он будет в одной точке, то чуть позже у него появится амплитуда того, что он будет в близлежащих точках. Уравнение дейст­вительно напоминает уравнения диффузии, которыми мы поль­зовались в начале курса. Но есть и одно важное отличие: мни­мый коэффициент перед производной по времени приводит к по­ведению, в корне отличному от обычной диффузии (например, от диффузии газа, распространяющегося по длинной трубе). Обычная диффузия приводит к действительным экспоненциаль­ным решениям, а решения (14.13) суть комплексные волны.

Дата добавления: 2015-06-04