Уравнение Шредингера. До сих пор мы просто заботились о том, как бы записать состояния, которые бы учитывали, что электрон может находить­ся в пространстве где угодно

До сих пор мы просто заботились о том, как бы записать состояния, которые бы учитывали, что электрон может находить­ся в пространстве где угодно. Теперь же следует позаботиться о включении в наше описание физики того, что может произойти в тех или иных обстоятельствах. Как и прежде, надо подумать о том, как состояния будут меняться со временем. Если у нас есть состояние |y>, которое несколько позже переходит в дру­гое состояние |y>, то положение в любой момент мы сможем описать, сделав волновую функцию (т. е. попросту амплитуду < r |y>) функцией не только координат, но и времени. Частицу в данных условиях можно будет тогда описывать, задавая меняющуюся во времени волновую функцию y (r, t) = y (х, у, z, t). Эта меняющаяся во времени волновая функция описывает эво­люцию последовательных состояний, которая происходит с тече­нием времени. Это так называемое «координатное представле­ние»; оно дает проекции состояния |y> на базисные состояния | r > и не всегда может считаться самым удобным, но мы с него

и начнем.

В гл. 6 мы описали на языке гамильтониана Н_ij., как состоя­ния меняются во времени. Мы видели, что временная вариация различных амплитуд дается матричным уравнением

Это уравнение говорит, что изменение во времени каждой из амплитуд С_i пропорционально сумме всех прочих амплитуд С_j

с коэффициентами Н_ij.

Как должно выглядеть (14.49) при континууме базисных состояний | x >? Вспомним сперва, что (14.49) можно также запи­сать в виде

Теперь ясно, что делать. Для x -представления следует писать

Сумма по базисным состояниям | j > заменяется интегралом по х'. Поскольку < х | Н^ | х' >должна быть какой-то функцией от x и х ', запишем ее как Н (х, х'), что соответствует Н _if в (14.49). Тогда (14.50) это то же самое, что

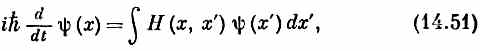
где

Согласно (14.51), быстрота изменения y в точке х зависела бы от значений y во всех других точках х '; множитель Н(х, х') — это амплитуда (в единицу времени) того, что электрон перепры­гнет из х' в x. Оказывается, однако, что в природе эта амплитуда всюду, кроме точек х', очень близких к х, равна нулю. Это озна­чает, как мы видели на примере цепочки атомов в начале главы [см. (14.12)], что правая часть (14.51) может быть полностью выражена только через y и ее производные по z в точке х.

Для частицы, которая свободно движется в пространстве, не подвергаясь действию каких-либо сил и возмущений, пра­вильный физический закон таков:

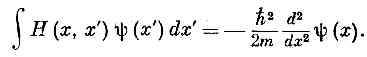
Откуда это получается? Это невозможно вывести из чего-либо нам уже известного. Это рождено в голове Шредингера, это вы­думано им в битве за понимание экспериментальных наблюдений реального мира. Может быть, какой-то ключ к тому, почему так должно быть, вам дадут размышления по поводу нашего вывода уравнения (14.12), которое проистекло из рассмотрения распро­странения электрона в кристалле.

Конечно, от свободных частиц проку мало. Что будет, если к частице приложить силы? Что ж, если действующая на частицу сила может быть описана с помощью скалярного потенциала V (х)(что означает, что речь идет не о магнитных силах, а об электрических) и если мы ограничимся низкими энергиями, чтобы иметь право пренебрегать теми сложностями, которые возникают при релятивистском движении, то гамильтониан, который укладывается в реальный мир, таков:

Опять-таки некоторый ключ к происхождению этого уравнения вы получите, если вернетесь к движению электрона в кристалле и посмотрите, как надо изменить уравнения, если энергия электрона медленно меняется от атома к атому, как если бы к кристаллу было приложено электрическое поле. Тогда член Е ₀ в (14.7) будет медленно меняться в зависимости от места и будет соответствовать новому слагаемому, появившемуся в (14.52). [Вас может удивить, отчего мы сразу перешли от (14.51) к (14.52), а не дали правильного выражения для амплитуды Н(х, х')=<х | Н^|х' >. Да потому, что Н (х, х') можно написать только с помощью необычных алгебраических функций, а инте­грал в правой части (14.51) выражается через привычные вещи. Если вам это в самом деле интересно, то вот смотрите: Н (х, х') можно записать так:

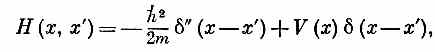
где d'' означает вторую производную 6-функции. Эту довольно странную функцию можно заменить чуть более удобным и пол­ностью ей равнозначным алгебраическим выражением

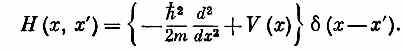
Мы не будем пользоваться этими формулами, а прямо будем рабо­тать с (14.52).]

Если теперь взять выражение (14.52) и подставить в (14.50) вместо интеграла, то для y(х) =<х |y> получится дифферен­циальное уравнение

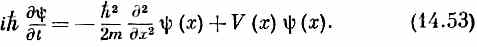
Совершенно очевидно, что надлежит поставить вместо (14.53),

если нас интересует трехмерное движение. Надо только d ² /dx ²

заменить на

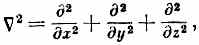
а V (х)заменить на V (x, у, z). Для электрона, движущегося в поле с потенциалом V (х, у, z), амплитуда y (х, у, z) удовлетво­ряет дифференциальному уравнению

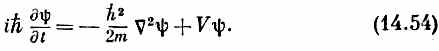
Называется оно уравнением Шредингера и было первым извест­ным квантовомеханическим уравнением. Его написал Шредин­гер, прежде чем было открыто любое другое описанное в этом томе уравнение.

Хотя мы здесь пришли к нему совсем иным путем, но появле­ние этого уравнения в 1926 г., когда Шредингер впервые его написал, явилось великим историческим моментом, отметившим рождение квантовомеханического описания материи. Многие годы внутренняя атомная структура вещества была великой тайной. Никто не был в состоянии понять, что скрепляет вещест­во, отчего существует химическая связь, и, особенно, как атомам удается быть устойчивыми. Хотя Бор и смог дать описание внут­реннего движения электрона в атоме водорода, которое, каза­лось бы, объясняло наблюдаемый спектр лучей, испускаемых этим атомом, но причина, отчего электроны движутся именно так, оставалась тайной. Шредингер, открыв истинные уравне­ния движения электронов в масштабах атома, снабдил нас тео­рией, которая позволила рассчитать атомные явления количест­венно, точно и подробно. В принципе его уравнение способно объяснить все атомные явления, кроме тех, которые связаны с магнетизмом и теорией относительности. Оно объясняет уровни энергии атома и все, что касается химической связи. Но, ко­нечно, это объяснение только в принципе. Математика вскоре становится столь сложной, что точно решить удается только простейшие задачи. Одни лишь атомы водорода и гелия были рассчитаны с высокой точностью. Однако путем различных при­ближений, порой весьма сомнительных, можно многое понять и в более сложных атомах и в химической связи молекул. Некоторые из этих приближений были показаны в предыдущих главах.

Уравнение Шредингера в том виде, в каком мы его записали, не учитывает каких-либо магнитных эффектов. Их, правда, можно приближенно принять во внимание, добавив в уравнение еще другие члены. Но, как мы убедились раньше, магнетизм — это эффект существенно релятивистский, так что правильное опи­сание движения электрона в произвольном электромагнитном поле можно обсуждать только в рамках надлежащего релятиви­стского уравнения. Правильное релятивистское уравнение для движения электрона было открыто Дираком через год после того, как Шредингер придумал свое уравнение; оно имеет со­вершенно другой вид. Мы его не успеем здесь изучить.

Прежде чем перейти к рассмотрению некоторых следствий из уравнения Шредингера, хотелось бы продемонстрировать, как оно выглядит для системы многих частиц. Мы не будем им пользоваться, а просто хотим показать вам его, чтобы подчерк­нуть, что волновая функция y не просто обычная волна в про­странстве, а функция многих переменных. Если частиц много, уравнение превращается в

Потенциальная функция V — это то, что классически соответст­вует полной потенциальной энергии всех частиц. Если на ча­стицы не действуют внешние силы, то функция V есть попросту электростатическая энергия взаимодействия всех частиц. Иначе говоря, если заряд i -й частицы равен Z_iq_e, то функция V просто равна

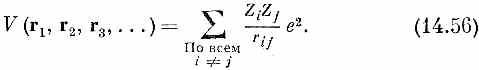
Дата добавления: 2015-06-04