Сложение моментов количества движения

Когда мы изучали сверхтонкую структуру атома водорода в гл. 10 (вып. 8), нам пришлось рассчитывать внутренние состоя­ния системы, составленной из двух частиц — электрона и протона — со спинами ¹/₂. Мы нашли, что четверка возможных спиновых состояний такой системы может быть разбита на две группы — на тройку состояний с одной энергией, которая во внешнем поле выглядела как частица со спином 1, и на одно ос­тавшееся состояние, которое вело себя как частица со спином 0. Иначе говоря, объединяя две частицы со спином ¹/₂, можно образовать систему, «полный спин» которой равен либо единице, либо нулю. В этом параграфе мы хотим рассмотреть на более общем уровне спиновые состояния системы, составленной из двух частиц с произвольными спинами. Это другая важная проблема, связанная с моментами количества движения квантовомеханической системы.

Перепишем сперва результаты гл. 10 для атома водорода в форме, которая позволит распространить их на более общий случай. Мы начали с двух частиц, которые теперь обозначим так: частица а (электрон) и частица b (протон). Спин частицы а был равен j_a (=¹/₂), a z-компонента момента количества движе­ния m_а могла принимать одно из нескольких значений (на са­мом деле два, а именно m_а =+¹/₂ или m_а=- ¹ / ₂). Точно так же спиновое состояние частицы b описывалось ее спином j_b и z-компонентой момента количества движения m_b. Из всего этого можно было составить несколько комбинаций спиновых состояний двух частиц. Например, из частицы а с m_а = ¹/₂ и частицы b с m_b =-¹/₂ можно было образовать состояние | а, +¹/₂; b, -¹/₂>. Вообще, объединенные состояния образовы­вали систему, у которой «спин системы», или «полный спин», или «полный момент количества движения» J мог быть равен либо единице, либо нулю, а z-компонента момента количества движения М могла равняться +1, 0 или -1 при J =1 и нулю при J =0. На этом новом языке формулы (10.41) и (10.42) можно переписать так, как показано в табл. 16.3.

Левый столбец таблицы описывает составное состояние через его полный момент количества движения J и z -компоненту М.

Таблица 16.3 • СОСТАВЛЕНИЕ МОМЕНТОВ КОЛИЧЕСТВА ДВИЖЕНИЯ ДВУХ ЧАСТИЦ СО СПИНОМ ¹/₂,

Правый столбец показывает, как составляются эти состояния из значений т двух частиц а и b.

Мы хотим обобщить этот результат на состояния, составлен­ные из двух объектов а и b с произвольными спинами j_а и j_b. Начнем с разбора примера, когда j_а =¹/₂ и j_b =1, а именно с атома дейтерия, в котором частица а — это электрон е, а части­ца b — ядро, т. е. дейтрон d. Тогда j_a = j_e= ¹ / ₂. Дейтрон обра­зован из одного протона и одного нейтрона в состоянии с пол­ным спином 1, так что j_b=j_d= 1. Мы хотим рассмотреть сверхтонкие состояния дейтерия, как мы сделали это для водо­рода. Поскольку у дейтрона может быть три состояния, m_b = m_d =+1, 0, -1, а у электрона — два, m_а = m_е =+¹/₂, -¹/₂, то всего имеется шесть возможных состояний, а именно (используется обозначение

| е, m_e; d, m_d >):

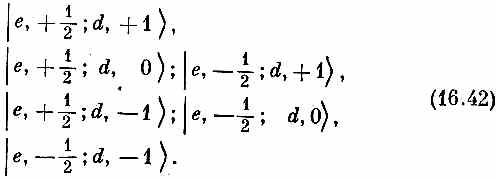
Обратите внимание, что мы разверстали состояния согласно значениям суммы m_e и m_d в порядке ее убывания.

Спросим теперь: что случится с этими состояниями, если спроецировать их в другую систему координат? Если эту новую систему просто повернуть вокруг оси z на угол j, то состояние | е, m_e; d, m_d >умножается на

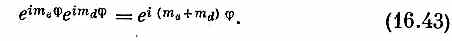
(Состояние можно считать произведением | е, m_е >| d, m_d >, и каждый вектор состояния независимо привнесет свой собст­венный экспоненциальный множитель.) Множитель (16.43) имеет форму е^iMj, поэтому z-компонента момента количества движения у состояния | е, m_е; d, m_d >окажется равной

M=m_e+m_d. (16.44)

Иначе говоря, z-компонента полного момента количества движения есть сумма z-компонент моментов количества движе­ния отдельных частей.

Значит, в перечне состояний (16.42) верхнее состояние имеет М =+³/₂, Два следующих М =+¹/₂, затем два М =-¹/₂и последнее состояние М=- ³/₂. Мы сразу же видим, что одной из возможностей для спина J объединенного состояния (для полного момента количества движения) должно быть ³/₂, это потребует четырех состояний с М= +³/₂, +¹/₂, -¹/₂ и - ³/₂. На М=+ ³/₂ есть только один кандидат, и мы сразу видим, что

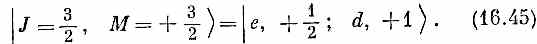
Но что является состоянием | J =³/₂, М =+¹/₂>? Кандидатов здесь два, они стоят во второй строчке (16.42), и всякая их ли­нейная комбинация тоже даст М= +¹/₂. Значит, в общем случае можно ожидать, что

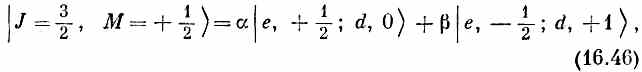
где a и b — два числа. Ихименуют коэффициенты Клебша — Гордона. Найти их и будет нашей очередной задачей.

И мы их легко найдем, если просто вспомним, что дейтрон состоит из нейтрона и протона, и в явном виде распишем со­стояния дейтрона, пользуясь правилами табл. 16.3. Если это проделать, то перечисленные в (16.42) состояния будут выгля­деть так, как показано в табл. 16.4.

Пользуясь состояниями из этой таблицы, мы хотим образо­вать четверку состояний с J =³/₂. Но ответ нам уже известен, потому что в табл. 16.1 уже стоят состояния со спином ³/₂, образованные из трех частиц со спином ¹/₂. Первое состояние в табл. 16.1 имеет | J =³/₂, М =+³/₂>, это |+++>, а в наших нынешних обозначениях это | e, +¹/₂; n, + ¹/₂; p, +¹/₂>, или первое состояние из табл. 16.4. Но это состояние — то же самое, что первое по списку в (16.42), так что наше выражение (16.45) подтверждается. Вторая строчка в табл. 16.1 утверждает, если воспользоваться нашими теперешними обозначениями, что

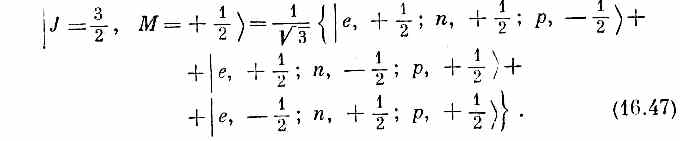
То, что стоит в правой части, можно, очевидно, составить из двух членов во второй строчке табл. 16.4, взяв Ö²/₃ от пер­вого члена и Ö¹/₃от второго. Иначе говоря, (16.47) эквива­лентно

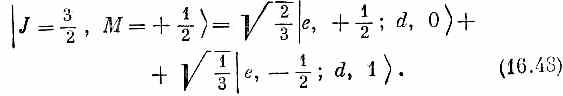
Таблица 16.4 • СОСТОЯНИЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ АТОМА ДЕЙТЕРИЯ

Мы нашли два наших первых коэффициента Клебша — Гор­дона a, и b [см. (16.46)]:

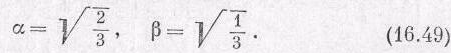
Повторяя ту же процедуру, найдем

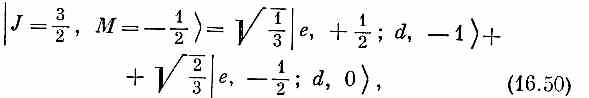
а также, конечно,

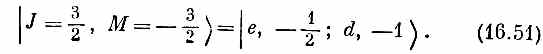
Это и есть правила составления из спина 1 и спина ¹/₂ полного спина J =³/₂. Мы свели (16.45) и (16.50) в табл. 16.5.

Таблица 16.5 • СОСТОЯНИЯ С J =³/₂ АТОМА ДЕЙТЕРИЯ

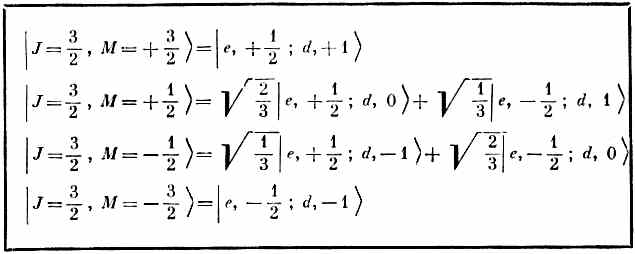
Но у нас пока есть только четыре состояния, а у системы, которую мы рассматриваем, их шесть.

Из двух состояний во второй строчке (16.42) мы для об­разования | J =³/₂, М =+¹/₂> составили только одну линей­ную комбинацию. Есть и другая линейная комбинация, орто­гональная к ней, у нее тоже М =+¹/₂ и она имеет вид

Точно так же из двух состояний в третьей строке (16.42) можно скомбинировать два взаимно-ортогональных состояния, каждое с М =- ¹/₂. То, которое ортогонально к (16.50), имеет вид

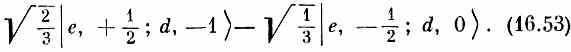
это и есть два оставшихся состояния. У них M=m_e+m_d= ±¹/₂; эти состояния должны соответствовать J =¹/₂. Итак, мы имеем

Можно убедиться, что эти два состояния действительно ведут себя как состояния объекта со спином ¹/₂; для этого надо выразить дейтронную часть через нейтронные и протонные со­стояния (при помощи табл. 16.3). Первое состояние в (16.53) превратится в

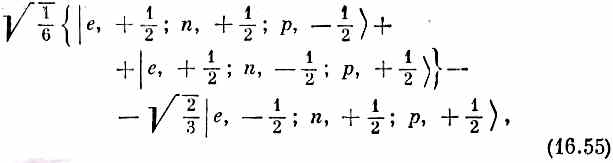
(16.55) а это можно переписать так:

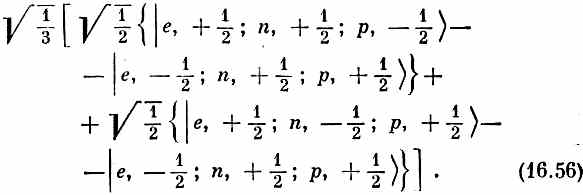
Посмотрите теперь на выражение в первых фигурных скобках и подумайте, что получается при объединении е и р. Вместе они образуют состояние с нулевым спином (см. нижнюю строку в табл. 16.3) и не дают вклада в момент количества движения. Остался только нейтрон, значит, вся первая фигурная скобка (16.56) будет вести себя при поворотах как нейтрон, а именно как состояние с J= ¹/₂, M=+ ¹/₂.

Повторяя те же рассуждения, убедимся, что во вторых фигурных скобках (16.56) электрон и нейтрон объединяются, чтобы образовать нулевой момент количества движения, и ос­тается только вклад протона — с m_p =+¹/₂. Скобка опять ведет себя как объект с J =+¹/₂, М =+¹/₂. Значит, и все выра­жение (16.56) преобразуется как | J =+¹/₂, М =+¹/₂>, чего мы и хотели. Состояние М= -¹/₂,отвечающее формуле (16.56), можно расписать так (заменив везде, где нужно, +¹/₂ на -¹/₂):

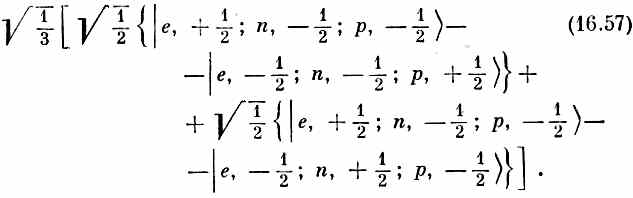
Вы легко проверите, что это совпадает со второй строчкой в (16.54), как и полагается, если каждая скобка представляет собой одно из двух состояний системы со спином ¹/₂. Значит, наши результаты подтвердились. Дейтрон и электрон могут существовать в шести спиновых состояниях, четыре из которых ведут себя как состояния объекта со спином ³/₂ (табл. 16.5), а два — как объект со спином ^J/₂ (16.54).

Результаты табл. 16.5 и уравнения (16.54) мы получили, вос­пользовавшись тем, что дейтрон состоит из нейтрона и протона. Правильность уравнений не зависит от этого особого обстоятель­ства. Для любого объекта со спином 1, объединяемого с объектом со спином ¹/₂, законы объединения (и коэффициенты) одни и те же. Совокупность уравнений в табл. 16.5 означает, что если система координат поворачивается, скажем, вокруг оси у, так что состояния частицы со спином ¹ / ₂и частицы со спином 1 изме­няются согласно табл. 16.1 и 16.2, то линейные комбинации по правую сторону знака равенства будут изменяться так, как это свойственно объекту со спином ³/₂. При таком же повороте со­стояния (16.54) будут меняться как состояния объекта со спи­ном ¹/₂. Результаты зависят только от свойств относительно пово­ротов (т. е. от спиновых состояний) двух исходных частиц, но отнюдь не от происхождения их моментов количества движения. Мы этим происхождением воспользовались лишь для вывода формул, выбрав частный случай, в котором одна из составных частей сама состоит из двух частиц со спином ¹/₂ в симметричном состоянии. Все наши результаты мы свели в табл. 16.6, изменив индексы е и d на а и b, чтобы подчеркнуть их общность.

Таблица 16.6 • ОБЪЕДИНЕНИЕ ЧАСТИЦЫ СО СПИНОМ ¹/₂(j_a=¹/₂) С ЧАСТИЦЕЙ СО СПИНОМ 1 (j_b =1)

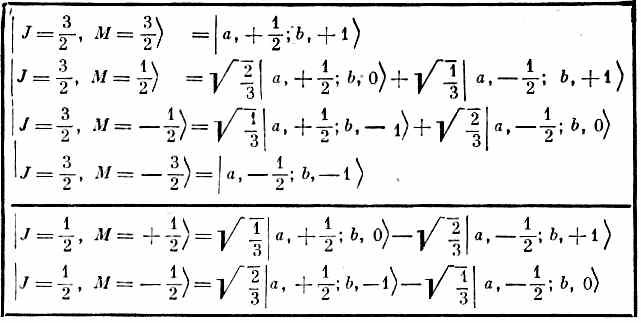
Поставим теперь себе общую задачу найти состояния, кото­рые можно образовать, объединяя два объекта с произвольными спинами. Скажем, у одного спин j_a (так что его z -компонента m_а пробегает 2 j_а +1 значений от - j_a до + j_a, а у другого j_b (с z-компонентой m_b, пробегающей значения от - j_b до+ j_b).

Объединенные состояния суть | а, m_а; b, m_b >, их всего (2 j_a +1)(2 j_b +1). Какие же состояния с полным спином / мы обнаружим?

Полная z-компонента М момента количества движения рав­няется m_а+m_b, и все состояния можно перечислить, опираясь на величину М [как в (16.42)]. Наибольшое М является единст­венным; оно отвечает значениям m_a=j_a и m_b=j_b и равно по­просту j_a+j_b. Это означает, что наибольший полный спин J также равен сумме j_а+j_b:

J = М _макс= j_a+j_b.

Следующему значению М, меньшему чем М _макс на единицу, будут соответствовать два состояния (либо m_а, либо m_b меньше своих максимальных значений на единицу). Из них должно быть образовано одно состояние, принадлежащее совокупности с J=j_a+j_b, и останется еще одно, которое будет принадлежать новой совокупности с J=j_a+j_b- 1. Следующее значение М (третье сверху) можно составить тремя путями (из m_a=j_a — 2, m_b = j_b, из m_a=j_a- 1, m_b=j_b- 1 и из m_a=j_a, m_b=j_b -2). Два из них принадлежат к уже начавшим составляться груп­пам; третье говорит нам, что надо включить в рассмотрение и со­стояния с J=j_a+j_b -2. Такие рассуждения будут продол­жаться до тех пор, пока уже нельзя будет, меняя то одно, то дру­гое т, получать новые состояния.

Пусть из j_а и j_b меньшим является j_b (а если они одинаковы, возьмите любое из них); тогда понадобятся только 2 j_b значений полного спина J, идущих единичными шагами от j_а+j_b вниз к j_а-j_b. Иначе говоря, когда объединяются два объекта со спинами j_а и j_b, то полный момент количества движения J их системы может равняться одному из значений:

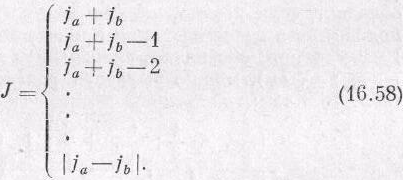
(Написав | j_a-j_b |вместо j_a-j_b, мы можем избежать напо­минания о том, что j_a³j_b.)

Для каждого из этих значений J имеется 2J+1 состояний с различными значениями М; М меняется от + J до - J. Каждое из них образовано из линейных комбинаций исходных состояний | а, m_а; b, m_b> с соответствующими коэффициентами — коэффициентами Клебша — Гордона для каждого отдельного члена. Можно считать, что эти коэффициенты дают «количест­во» состояния | j_a, m_a; j_b, m_b>, проявляющегося в состоянии

Таблица 16.7 • ОБЪЕДИНЕНИЕ ДВУХ ЧАСТИЦ СО СПИНОМ 1 (j_a =1, j_b =1)

I /, My. Так что каждый из коэффициентов Клебша — Гордона обладает, если угодно, шестью индексами, указывающими его положение в формулах типа приведенных в табл. 16.3 и 16.6. Иначе говоря, обозначая, скажем, эти коэффициенты С (J, М; j_a, m_a; j_b, m_b), можно выразить равенство во второй строчке табл. 16.6 так:

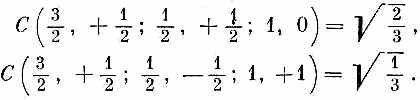
Мы не будем здесь подсчитывать коэффициенты для других частных случаев. Но вы обнаружите такие таблицы во мно­гих книжках. Попробуйте сами подсчитать другой случай, например объединение двух объектов со спином 1. Мы же про­сто привели в табл. 16.7 окончательный результат.

Эти законы объединения моментов количества движения имеют очень важное значение в физике частиц, их приложениям поистине нет конца. К сожалению, у нас нет сейчас больше вре­мени на другие примеры.

Дата добавления: 2015-06-04