Сферически симметричные решения

Попробуем сперва отыскать какую-нибудь функцию попроще, чтобы она удовлетворяла уравнению (17.7). Хотя волновая функция y в общем случае будет зависеть как от q и j, так и от r, можно все же поискать, не бывает ли такого особого случая, когда y не зависит от углов. Если волновая функция от углов не зависит, то при поворотах системы координат ни одна из амплитуд никак не будет меняться. Это означает, что все ком­поненты момента количества движения равны нулю. Такая функция y должна соответствовать состоянию с равным нулю полным моментом количества движения. (На самом деле, ко­нечно, равен нулю только орбитальный момент количества дви­жения, потому что остается еще спин электрона, но мы на эту часть момента не обращаем внимания.) Состояние с нулевым орбитальным моментом количества движения имеет особое на­звание. Его называют «s-состоянием» (можете считать, что s от слова «сферически симметричный»).

Раз y не собирается зависеть от q и j, то в полном лапласиане останется только один первый член и (17.7) сильно упростится:

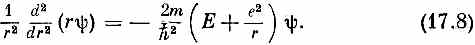
• Прежде чем заняться решением подобного уравнения, хорошо

; бы, изменив масштаб, убрать из него все лишние константы

вроде е², m, h. От этого выкладки станут легче. Если сделать подстановки

то уравнение (17.8) обратится (после умножения на r) в

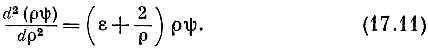
Эти изменения масштаба означают, что мы измеряем расстояние r и энергию Е в «естественных» атомных единицах. Например, r= r/r_B, где r_B=h²/me ², называется «боровским радиусом» и равно примерно 0,528 Å. Точно так же e =E/E_R, где E_R=me ⁴ /2h ². Эта энергия называется «ридбергом» и равна примерно 13,6 эв. Раз произведение ry встречается в обеих частях уравнения, то лучше работать с ним, чем с самим y. Обозначив

ry= f, (17.12)

мы получим уравнение, которое выглядит проще:

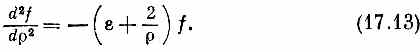
Теперь нам предстоит найти функцию f, которая удовлет­воряет уравнению (17.13), иными словами, просто решить диф­ференциальное уравнение. К сожалению, не существует ника­ких общих, годных во всех случаях жизни методов решения любого дифференциального уравнения. Вы должны просто по­крутить его то так, то этак. Хоть уравнение не из легких, но лю­ди все же нашли, что его можно решить при помощи следующей процедуры. Первым делом вы заменяете f, которое является некоторой функцией от r, произведением двух функций:

Это просто означает, что вы выносите из f (r) множитель е^-ar. Для любого f (r) это можно сделать. Задача теперь просто све­лась к отысканию подходящей функции g (r).

Подставив (17.14) в (17.13), мы получим следующее уравне­ние для g:

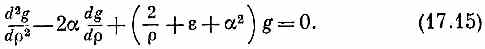
Мы вправе выбрать любое a, поэтому сделаем так, чтобы было

a²=-e; (17.16)

тогда получим

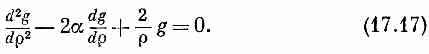
Вы можете подумать, что мы не так уж далеко ушли от урав­нения (17.13); но новое уравнение тем хорошо, что его можно легко решить разложением g (r) в ряд по r. В принципе есть возможность таким же способом решать и (17.13), но только все проходит сложнее. Мы говорим: уравнению (17.17) можно удов­летворить некоторой функцией g (r), которая записывается в виде ряда

где a_k— постоянные коэффициенты. И нам осталось только найти подходящую бесконечную последовательность коэффициентов! Проверим, годится ли такая запись решения, Первая производ­ная такой функции g (r) равна

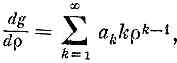
а вторая

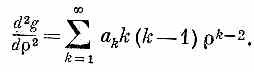
Подставляя это в (17:17), имеем

Пока еще не ясно, вышло ли у нас что-нибудь; но мы рвемся вперед. Если мы первую сумму заменим некоторым ее эквива­лентом, то все выражение станет выглядеть лучше. Первый член в сумме равен нулю, поэтому каждое k можно заменить на k +1, от этого ничего в бесконечном ряде не изменится. Значит, пер­вую сумму мы вправе записать и так:

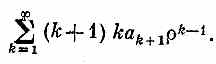
Теперь можно объединить все три суммы в одну:

Этот степенной ряд должен обращаться в нуль при всех мыслимых значениях r, что возможно лишь тогда, когда коэф­фициенты при каждой степени r порознь равны нулю. Мы полу­чим решение для атома водорода, если отыщем такую последо­вательность a_k, для которой

при всех k >1. А это, конечно, устроить легко. Выберите какое угодно а ₁. Затем все прочие коэффициенты образуйте с помощью формулы

Пользуясь ею, вы получите а ₂, а ₃, а ₄ и т. д., и каждая пара будет, конечно, удовлетворять (17.21). Мы получим ряд для g (r), удовлетворяющий (17.17). С его помощью мы напишем y — решение уравнения Шредингера. Обратите внимание, что решения зависят от того, какова предполагаемая энергия (через a), но для каждого значения e получается свой ряд. Решение-то у нас есть, но что оно представляет физически? Понятие об этом мы получим, поглядев, что происходит вдалеке от протона — при больших r. Там основное значение приобре­тают наивысшие степени членов ряда, т. е. нам надо посмотреть, что бывает при больших k. Когда k>>1, то уравнение (17.22) приближенно совпадает с:

а это означает, что

Но это как раз коэффициенты разложения в ряд е^+2ar. Функ­ция g оказывается быстро растущей экспонентой. Даже после умножения на е^-ar получающаяся функция f (r) [см. (17.14)] будет при больших r меняться как е^ar. Мы нашли математиче­ское решение, но оно не является физическим. Оно представляет случай, когда электрону менее всего вероятно очутиться вблизи протона! Чаще всего он вам повстречается на очень больших расстояниях р. А волновая функция для связанного электрона должна при больших r стремиться к нулю.

Придется подумать, нельзя ли как-нибудь обмануть решение. Оказывается, можно. Посмотрите! Если бы, по счастью, оказа­лось, что a = 1 /n, где n — любое целое число, то уравнение (17.22) привело бы к a _n+1=0. И все высшие члены обратились бы тоже в нуль. Вышел бы не бесконечный ряд, а конечный многочлен. Любой многочлен растет медленнее, чем е^ar, поэтому множитель е^-a наверняка забьет его при больших r, и функ­ция f при больших r будет стремиться к нулю. Единственные решения для связанных состояний это те, для которых a=1/n, где n =1, 2, 3, 4 и т. д.

Оглядываясь на уравнение (17.16), мы видим, что у сфериче­ски симметричного волнового уравнения могут существовать решения для связанных состояний лишь при энергиях

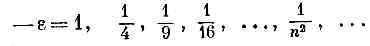
Допустимы только те энергии, которые составляют именно такую часть ридберга Е_R=me ⁴ /2h ², т. е. энергия n -го уровня равна

Кстати, ничего мистического в отрицательных энергиях нет. Они отрицательны просто потому, что когда мы решили писать V= -е²/r, то тем самым в качестве нуля энергии выбрали энергию электрона, расположенного вдалеке от протона. Когда он ближе, то его энергия меньше, т. е. ниже нуля. Энергия ни­же всего (самая отрицательная) при n =1и возрастает к нулю с ростом п.

Еще до открытия квантовой механики экспериментальное изучение спектра водорода показало, что уровни энергии описы­ваются формулой (17.24), где Е_R, как это следует из измерений, равно примерно 13,6 зв. Затем Бор придумал модель, которая привела к тому же уравнению (17.24) и предсказала, что E_R должно равняться me ⁴ / 2 h ². Первым большим успехом теории Шредингера явилось то, что она смогла воспроизвести этот результат прямо из основного уравнения движения электрона.

Теперь, когда мы рассчитали наш первый атом, давайте рас­смотрим свойства полученного нами решения. Объединим все выделившиеся по дороге факторы и выпишем окончательный вид решения:

где

и

Пока нас интересует главным образом относительная вероят­ность обнаружить электрон в том или ином месте, можно в ка­честве а ₁выбирать любое число. Возьмем, например, а ₁=1. (Обычно выбирают а ₁так, чтобы волновая функция была «нор­мирована», т. е. чтобы полная вероятность обнаружить элек­трон где бы то ни было в атоме была равна единице. Мы в этом сейчас не нуждаемся.)

В низшем энергетическом состоянии n =1 и

Если атом водорода находится в своем основном (наиболее низ­ком энергетическом) состоянии, то амплитуда того, что элект­рон будет обнаружен в каком-то месте, экспоненциально падает с расстоянием от протона. Вероятнее всего встретить его вплотную близ протона. Характерное расстояние, на котором он встречается, составляет около одного r, или одного боровского радиуса r_B.

Подстановка n =2 дает следующий более высокий уровень. В волновую функцию этого состояния входят два слагаемых. Она равна

Волновая функция для следующего уровня равна

Эти три волновые функции начерчены на фиг. 17.2.

Фиг. 17.2. Волновые функции трех первых состоя­ний атома водорода с l =0. Масштабы выбраны так, чтобы полные вероятности совпадали.

Общая тен­денция уже видна. Все волновые функции при больших r, поко­лебавшись несколько раз, приближаются к нулю. И действи­тельно, число «изгибов» у y _n как раз равно n, или, если угодно, число пересечений оси абсцисс — число нулей — равно n- 1.

Дата добавления: 2015-06-04