Добавление 1. Вывод матрицы поворота

Для тех, кто хотел бы разобраться в этом поподробнее, мы вычислим сейчас общую матрицу поворота для системы со спи­ном (полным моментом количества движения) j. В расчете об­щего случая на самом деле большой необходимости нет; важно понять идею, а все результаты вы сможете найти в таблицах, которые приводятся во многих книжках. Но, с другой стороны, вы зашли уже так далеко, что у вас, естественно, может возник­нуть желание убедиться, что вы и впрямь в состоянии понять даже столь сложные формулы квантовой механики, как (16.35).

Расширим рассуждения § 4 на систему со спином j, которую будем считать составленной из 2/ объектов со спином ¹/₂. Состоя­ние с m=j имело бы вид | + + +... +> (с j плюсами). Для m=j- 1 было бы 2 j членов типа | + +... + + ->, | + +... +- +>и т. д. Рассмотрим общий случай, когда имеет­ся r плюсов и s минусов, причем r + s =2 j. При повороте вокруг оси r от каждого из r плюсов появится множитель e^+ij/2. В итоге фаза изменится на i (r /2- s /2)j. Мы видим, что

m=(r-s)/ 2. (16.59)

Как и в случае J =³/₂, каждое состояние с определенным т должно быть суммой всех состояний с одними и теми же r и s, взятых со знаком плюс, т. е. состояний, отвечающих всевозмож­ным перестановкам с r плюсами и s минусами. Мы считаем, что вам известно, что всего таких сочетаний есть (r+s)!/r!s!. Чтобы нормировать каждое состояние, надо эту сумму разделить на корень квадратный из этого числа. Можно написать

где

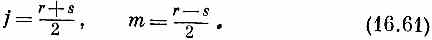
Введем еще новые обозначения, они нам помогут в счете. Ну а поскольку мы уж определили состояния при помощи (16.60), то два числа r и s определяют состояние ничуть не хуже, чем j и m. Мы легче проследим за выкладками, если обозначим

где [см.. (16.61)]

r = j+m, s = j-т.

Далее, (16.60) мы запишем, пользуясь специальным обозна­чением

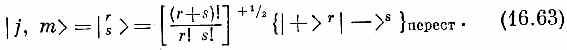
Обратите внимание, что показатель степени в общем множителе мы изменили на +¹/₂. Это оттого, что внутри фигурных скобок в (16.60) стоит как раз N =(r+s)!/r!s! слагаемых. Если сопоста­вить (16.63) с (16.60), то ясно, что

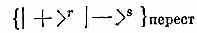— это краткая запись выражения

где N — количество различных слагаемых в скобках. Эти обо­значения удобны тем, что каждый раз при повороте все знаки плюс вносят один и тот же множитель, так что в итоге он полу­чается в r -й степени. Точно так же все знаки минус дадут некоторый множитель в s -й степени, в каком бы порядке эти знаки ни стояли.

Теперь положим, что мы повернули нашу систему вокруг оси у на угол q. Нас интересует 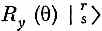. Оператор R_y (q), дей­ствуя на каждый |+>, дает

где С =cosq/2 и S= sin q/2. Когда же R_y (q) действует на | ->, это приводит к

Так что искомое выражение равно

Теперь надо возвысить биномы в степень и перемножить. По­явятся члены со всеми степенями |+ у от нуля до r+s. Посмот­рим, какие члены дадут r'-ю степень |+). Они всегда будут сопровождаться множителем типа |->^s', где s '=2 j - r'. Соберем их вместе. Получится сумма членов типа |+>^r' |->^s' с численными коэффициентами А_r' , куда входят коэффициенты биномиального разложения вместе с множителями С и S. Урав­нение (16.65) тогда будет выглядеть так:

Теперь разделим каждое А_r' на множитель [ (r'+s')\ l r'! s'!] ^l/2 и обозначим частное через В_r . Тогда (16.66) превратится в

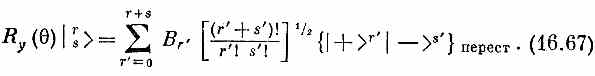
[Можно просто сказать, что требование, чтобы (16.67) совпадало с (16.65), определяет B_{r ’}]

Если так определить В_r' , то оставшиеся множители в правой части (16.67) будут как раз состояниями 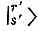. Итак, имеем

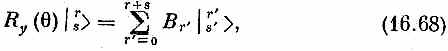
где s' всегда равняется r+s - r'. А это, конечно, означает, что коэффициенты В_r' и есть искомые матричные элементы

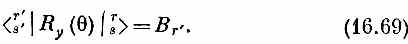
Теперь, чтобы найти B _r', остается немного: лишь про­биться через алгебру.

Сравнивая (16.67) с (16.65) и вспоминая, что r'+s'=r+s, мы видим, что B_{r '} — это просто коэффициент при a^r'b^s' в вы­ражении

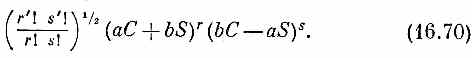
Осталась лишь нудная работа разложить скобки по биному Ньютона и собрать члены с данными степенями а и b. Если вы все это проделаете, то увидите, что коэффициент при а^r'b^s' в (16.70) имеет вид

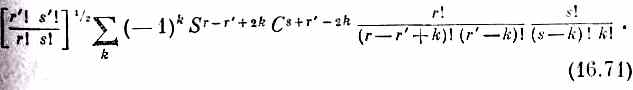
Сумма берется по всем целым k, при которых аргументы факто­риалов больше или в крайнем случае равны нулю. Это выраже­ние и есть искомый матричный элемент.

В конце надо вернуться к нашим первоначальным обозначе­ниям j, m и m', пользуясь формулами

r=j+-m, r'=j+m', s=j-m, s'=j-m'. Проделав эти подстановки, получим уравнение (16.34) из § 4.

Дата добавления: 2015-06-04