Операции и операторы

Изменение средних со временем

Момент коли­чества движения

Оператор импульса

Оператор места

Средняя энергия атома

Средние энергии

Операции и операторы

ОПЕРАТОРЫ

В действительности мнение об инертности благородных газов ока­залось, как и многое другое, сильным преувеличением. Криптон, напри­мер, весьма охотно соединяется с фтором, образуя кристаллы KrF6. Сейчас химия инертных газов превращается в большую и увлекательную науку.— Прим. ред.

* Это нетрудно вывести из (16.35). Но можно это сделать, исходя из основных принципов; надо только воспользоваться идеями, изложенными в гл. 16, § 4. Состояние |l, l> может быть составлено из 2l частиц со спином ¹/₂, у которых спин направлен вверх; а в состоянии |l, 0> l спинов было бы направлено вверх, а l — вниз. При повороте амплитуда того, что спин останется тем же, равна cosq/2, а амплитуда того, что он перевернется, равна sin q/2. А нас интересует амплитуда того, что l спинов не перевер­нутся, а другие l перевернутся. Такая амплитуда равна (cosq/2sinq/2)^l, а это то же самое, что sin^lq.

* Поскольку это и другие особые наименования являются частью общепринятого словаря атомной физики, вам попросту придется выучить их. Мы вам поможем их запомнить, поместив в этой главе небольшой «словарик» подобных терминов.

* Как обычно,

Глава 18

Для того чтобы управиться со всем, что мы до сих пор делали в квантовой механике, достаточно было бы обычной алгебры, но мы все же время от времени демонстрировали особые способы записи квантовомеханических величин и уравнений. Мы хотели бы рассказать теперь немного больше о некоторых интересных и по­лезных способах описания квантовомеханических величин.

К предмету квантовой механики можно подойти разными способами, и во многих книгах прибегают совсем к иному подходу, чем у нас. Когда вы начнете читать другие книжки, то может оказаться, что вам не удастся сразу связать то, что в них говорится, с тем, что де­лали мы. Хотя в этой главе мы и получим кое-какие новые результаты, она не похожа на дру­гие главы. У нее совсем иная цель: рассказать о других способах выражения тех же самых фи­зических представлений. Зная это, вы легче поймете, о чем говорится в других книжках. Когда люди впервые начали разрабатывать классическую механику, они неизменно распи­сывали свои уравнения через х-, у- и z -компоненты. Затем кто-то сделал шаг вперед в указал, что все можно упростить, введя век­торные обозначения. Правда, очень часто, чтобы представить себе задачу конкретнее, вы разбиваете векторы обратно на их компонен­ты. Но обычно все же куда легче делать расчеты и разбираться в существе дела, работая с век­торами. В квантовой механике нам тоже удалось упростить запись многих вещей, воспользовав­шись идеей «вектора состояния». Вектор состоя­ния |y> ничего общего, конечно, не имеет с геометрическими векторами в трехмерном пространстве; это просто отвлеченный символ, который обозначает физиче­ское состояние, отмечаемое своим «значком» или «назва­нием» y. Представление это весьма и весьма полезно, потому что на языке этих символов законы квантовой механики выглядят как алгебраические уравнения. К примеру, тот наш фундаментальный закон, что всякое состояние можно соста­вить из линейной комбинации базисных состояний, записы­вается так:

где С_i — совокупность обычных (комплексных) чисел, ампли­туд C_i =<i|y>, а |1>, |2>, |3> и т. д. обозначают базисные состояния в некотором базисе, или представлении.

Если вы берете какое-то физическое состояние и что-то про­делываете над ним (поворачиваете или ждете в течение времени At или еще что-то), то вы получаете уже другое состояние. Мы говорим: «производя над состоянием операцию, получаем новое состояние». Эту же идею можно выразить уравнением

Операция над состоянием создает новое состояние. Оператор А обозначает некоторую определенную операцию. Когда эта операция совершается над каким-то состоянием, скажем над |y>, то она создает какое-то другое состояние |j>.

Что означает уравнение (18.2)? Мы определяем его смысл так. Умножив уравнение на < i | и разложив |y> по (18.1), вы получите

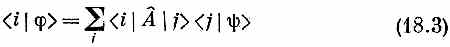
(| j > — это состояния из той же совокупности, что и | i >. Теперь это просто алгебраическое уравнение. Число < i |j> показывает, какое количество базисного состояния | i > вы обнаружите в |j>, и оно определяется через линейную суперпо­зицию амплитуд < j |y> того, что вы обнаружите |y> в том или ином базисном состоянии. Числа < i|A ^| j > — это попросту коэф­фициенты, которые говорят, сколько (какая доля) состояния < j |y> входит в сумму. Оператор А численно описывается на­бором чисел, или «матрицей»

Значит, (18.2) это запись уравнения (18.3) на высшем уровне. А на самом деле даже немножко и сверх того: в нем подразуме­вается нечто большее. В (18.2) нет ссылки на ту или иную систе­му базисных состояний. Уравнение (18.3) — это образ уравнения (18.2) в некоторой системе базисных состояний. Но, как известно, система годится любая. Именно это и имеется в виду в (18.3). Операторная манера записи, стало быть, уклоняется от того или иного выбора системы. Конечно, если вам хочется определенности, вы вольны избрать одну из систем. И когда вы де­лаете этот выбор, вы пишете уравнение (18.3). Значит, опера­торное уравнение (18.2) — это более отвлеченный способ за­писи алгебраического уравнения (18.3). Это очень походит на разницу между записью

c=aXb и записью

Первый способ нагляднее. Но если вам понадобятся числа, вы наверняка зададите сперва компоненты относительно некоторой системы осей. Точно так же, если вы хотите дать понять, что за штука А, вам нужно быть готовыми задать матрицу А_ij через некоторую совокупность базисных состояний. И пока вы имеете в виду определенную совокупность чисел a_ij, уравнение (18.2) означает то же, что и (18.3). (И нужно еще помнить, что если уж вы знаете матрицу для одной частной совокупности ба­зисных состояний, то всегда сможете подсчитать матрицу, соот­ветствующую любому другому базису. Матрицу всегда можно преобразовать от одного представления к другому.)

Операторное уравнение (18.2) допускает и другие возмож­ности. Если мы представили себе некоторый оператор А, то его можно применить к любому состоянию |y> и он создаст новое состояние A^ |y>. Временами получаемое таким путем «состоя­ние» может оказаться очень своеобразным — оно может уже не представлять собой никакой физической ситуации, с которой можно встретиться в природе. (Например, может получиться состояние, которое не нормировано на вероятность получить один электрон.) Иными словами, временами мы можем получить «состояния», которые есть математически искусственные обра­зования. Эти искусственные «состояния» могут все равно ока­заться полезными, чаще всего в каких-либо промежуточных вы­числениях.

Мы уже приводили много примеров квантовомеханических операторов. Встречался нам оператор поворота R ^_у(q), который, взяв состояние |y>, делает из него новое состояние, представ­ляющее собой старое состояние с точки зрения повернутой сис­темы координат. Встречался оператор четности (или инверсии)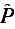

, создающий новое состояние обращением всех координат. Встре­чались и операторы s _х, s _у и s _z для частиц со спином ¹/₂.

Оператор J ^_z определялся в гл. 15 через оператор поворота на малые углы e:

Это, конечно, попросту означает, что

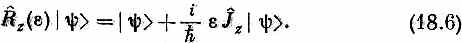
В этом примере J ^_z|y> — это умноженное на h/i e состояние, получаемое тоща, когда вы повернете |y> на малый угол e и затем вычтете прежнее состояние. Оно представляет «состоя­ние», являющееся разностью двух состояний.

Еще один пример. Мы имели оператор р^_х, он назывался опе­ратором (x -компоненты) импульса и определялся уравнением, похожим на (18.6). Если D^_x (L) — оператор, который смещает состояние вдоль х на длину L, то р^_х определялось так:

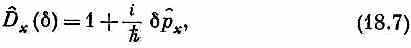
где d — малое смещение. Смещение состояния |y> вдоль оси х на небольшое расстояние d дает новое состояние |y'>. Мы го­ворим, что это новое состояние есть старое состояние плюс еще новый кусочек

Операторы, о которых мы говорим сейчас, действуют на вектор состояния, скажем на |y>, являющийся абстрактным описанием физической ситуации. Это совсем не то, что алгебра­ические операторы, действующие на математические функции. Например, d/dx это «оператор», действие которого на f (x)соз­дает из f (x)новую функцию f' (x) =df/dx. Другой пример ал­гебраического оператора — это Ѳ. Можно понять, отчего в обоих случаях пользуются одним и тем же словом, но нужно помнить, что это разные типы операторов. Квантовомеханический оператор А действует не на алгебраическую функцию, а на вектор состояния, скажем на |y>. В квантовой механике употребляются и те и другие операторы, и часто, как вы уви­дите, в уравнениях сходного типа.

Когда вы впервые изучаете предмет, то все время надо иметь в виду эту разницу. А позднее, когда предмет вам станет ближе, вы увидите, что не так уж важно делать резкое различие между одними операторами и другими. И во многих книгах, как вы убедитесь, оба типа операторов обозначаются одинаково!

Теперь нам пора продвинуться вперед и узнать о мно­гих полезных вещах, которые можно проделывать с помощью операторов. Но для начала небольшое замечание. Пускай у нас имеется оператор А^, матрица которого в каком-то базисе есть A_ij=<i | A^ | j >. Амплитуда того, что состояние A ^|y> находится также в некотором другом состоянии |j>, есть <j| A ^|y>. Имеет ли смысл комплексное сопряжение этой амплитуды? Вы, вероятно, сможете показать, что

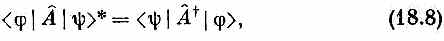
где А^⁺ (читается «А с крестом») это оператор, матричные эле­менты которого равны

A⁺_ij =(A_ji)*. (18.9)

Иначе говоря, чтобы получить i, j -и элемент матрицы А⁺, вы обращаетесь к j, i -му элементу матрицы А (индексы пере­ставлены) и комплексно его сопрягаете. Амплитуда того, что состояние А^⁺ |j> находится в состоянии |y>, комплексно сопряжена амплитуде того, что А^ |y> находится в |j>. Опера­тор А^⁺ называется «эрмитово сопряженным» оператору А^. Мно­гие важные операторы квантовой механики имеют специальное свойство: если вы их эрмитово сопрягаете, вы опять возвращае­тесь к тому же оператору. Если В как раз такой оператор, то В^⁺=В^;его называют «самосопряженным», или «эрмитовым», оператором.

Дата добавления: 2015-06-04