Явление Мейсснера

Теперь уже можно кое-что рассказать и о явлении сверхпро­водимости. Прежде всего здесь отсутствует электрическое сопротивление. А нет сопротивления оттого, что все электроны коллективно пребывают в одинаковом состоянии. При обычном течении тока то один электрон, то другой выбивается из равно­мерного потока, постепенно разрушая полный импульс. Здесь же не так-то просто помешать одному электрону делать то, что делают другие, ибо все бозе-частицы стремятся попасть в оди­наковое состояние. Ток, если уж он пошел, то это навеки.

Легко также понять, что если имеется кусок металла в сверхпроводящем состоянии и вы включите не очень сильное магнит­ное поле (что будет, когда оно сильное, мы обойдем молчанием), то оно не сможет проникнуть в металл. Если бы в момент созда­ния магнитного поля хоть какая-то его часть возросла внутри металла, то в нем появилась бы скорость изменения потока, а в результате и электрическое поле, которое в свою очередь немедленно вызвало бы электрический ток, который, по закону Ленца, был бы направлен на уменьшение потока. А раз все электроны будут двигаться совместно, то бесконечно малое элек­трическое поле уже вызовет достаточный ток, чтобы полностью воспротивиться наложению любого магнитного поля. Значит, если вы включите поле после того как охладили металл до сверхпроводящего состояния, внутрь оно допущено ни за что не будет.

Еще интереснее другое связанное с этим явление, экспери­ментально обнаруженное Мейсснером. Если имеется кусок металла при высокой температуре (т. е. обычный проводник) и в нем вы создали магнитное поле, а затем снизили температуру ниже критического уровня (когда металл становится сверх­проводником), то поле будет вытолкнуто. Иными словами, в сверхпроводнике возникает свой собственный ток, и как раз в таком количестве, чтобы вытолкнуть поле наружу.

Причину этого можно понять из уравнений, и сейчас я объяс­ню как. Пусть у нас имеется сплошной кусок сверхпроводящего материала (без отверстий). Тогда в любом установившемся положении дивергенция тока должна быть равна нулю, потому что ему некуда течь. Удобно будет выбрать дивергенцию А рав­ной нулю. (Конечно, полагалось бы объяснить, отчего принятие этого соглашения не означает потери общности, но я не хочу тратить на это время.) Если взять дивергенцию от уравнения (19.18), то в итоге окажется, что лапласиан от q должен быть ра­вен нулю. Но погодите, а как же с вариацией r? Я забыл упо­мянуть об одном важном пункте. В металле существует фон по­ложительных зарядов (из-за наличия атомных ионов решетки). Если плотность заряда r однородна, то не будет ни остаточного заряда, ни электрического поля. Если бы в каком-то месте электроны и скопились, то их заряд не был бы нейтрализован и возникло бы сильнейшее отталкивание, которое растолкало бы электроны по всему металлу. Значит, в обычных обстоятель­ствах плотность электронного заряда в сверхпроводниках поч­ти идеально однородна, и я вправе считать r постоянным. Да­лее, единственная возможность, чтобы Ѳq было равно нулю всюду внутри сплошного куска металла,— это постоянство q. А это означает, что в J не входит член с р -импульсом. Согласно выражению (19.18), ток пропорционален r, умноженному на А. Значит в куске сверхпроводящего материала ток с необходимо­стью будет пропорционален вектор-потенциалу

Знаки r и q одинаковы (отрицательны), и поскольку r — вели­чина постоянная, то я могу положить r q / m =-(некоторая по­стоянная). Тогда

J =-(некоторая постоянная) А. (19.21)

Это уравнение впервые предложили братья Лондон, чтобы объяснить экспериментальные наблюдения над сверхпроводи­мостью, задолго до того, как люди уяснили себе квантовомеханическое происхождение эффекта.

Мы теперь можем подставить (19.20) в уравнения электро­магнетизма и определить поля. Векторный потенциал связан с плотностью тока уравнением

Если вместо J я подставлю (19.21), то получу

где l²—просто новая постоянная

Теперь можно попробовать решить это уравнение относи­тельно А и детальнее посмотреть, что там происходит. Напри­мер, в одномерном случае у (19.23) имеются экспоненциальные решения вида е^-lx и е ^{+ lх}. Эти решения означают, что вектор­ный потенциал обязан экспоненциально убывать по мере удале­ния от поверхности внутрь образца. (Возрастать он не может — будет взрыв.) Если кусок металла очень велик по сравнению с 1/l, то поле проникнет внутрь только в тонкий слой у поверх­ности толщиной около 1/l. Все остальное место внут­ри проводника будет сво­бодно от поля, как пока­зано на фиг. 19.3.

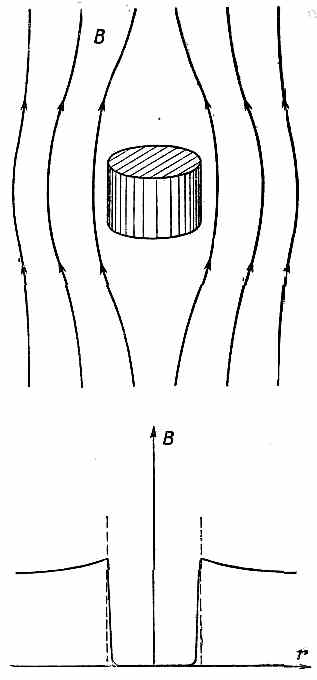
Фиг. 19.3. Сверхпроводящий цилиндр в магнитном поле (а) и магнитное поле В как функ­ция от r (б).

Этим и объясняется явление Мейсснера.

Какова же эта «глубина проникновения» 1/l? Вы помните, что r ₀— «электро­магнитный радиус» элек­трона (2,8•10^-13 см)—вы­ражается формулой

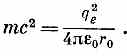
Вы помните также, что q вдвое больше заряда электрона, так что

Записав r в виде q_eN, где N — число электронов в кубическом сантиметре, мы получим

У такого металла, как свинец, на каждый кубический сантиметр приходится 3•10²² атомов, и если каждый атом снабдит нас одним электроном проводимости, то 1/l будет порядка 2•10^-5 см. Это дает вам порядок величины эффекта.

Дата добавления: 2015-06-04