Динамика сверхпроводимости

Эффект Мейсснера и квантование потока подтверждают наши общие представления. Для полноты стоит еще продемонстри­ровать, как с этой точки зрения выглядели бы полные уравне­ния сверхпроводящей жидкости,— получается довольно инте­ресно. До сих пор я подставлял выражение для yтолько в урав­нения плотности заряда и тока. Но если я их подставлю в полное уравнение Шредингера, то получу уравнения для r и q. Интересно поглядеть, что из этого выйдет, потому что перед нами сейчас «жидкость» электронных пар с плотностью заряда r и с таинственной q; мы можем посмотреть, как выглядят уравнения такой «жидкости»! Итак, подставим волновую функ­цию (19.17) в уравнение Шредингера (19.3) и вспомним, что r и q это вещественнее функции от х, у и z. Если мы отделим вещественную часть от мнимой, то уравнений станет два. Чтобы запись была короче, я, следуя уравнению (19.19), напишу

Тогда одно из двух уравнений примет вид

Поскольку rv это и есть J [см. (19.18)], то мы просто еще раз получили уравнение непрерывности. Второе же уравнение говорит об изменении q:

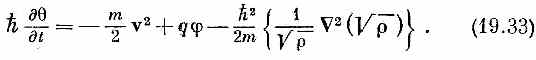
Те из вас, кто хорошо знаком с гидродинамикой (думаю, очень немногие), в этом уравнении узнают уравнение движения электрически заряженной жидкости, если только отождествить h q с «потенциалом скоростей»; но только в последнем члене, который должен быть энергией сжатия жидкости, имеется до­вольно странная зависимость от плотности р. Во всяком случае, это уравнение утверждает, что скорость изменения величины h qдается членом с кинетической энергией (т/2)v² плюс член с потенциальной энергий q j плюс добавочный член с множите­лем h ², который мы назовем «квантовомеханической энергией». Мы видели, что внутри сверхпроводника электростатические силы поддерживают r очень однородным, поэтому во всех прак­тических применениях этим членом почти наверняка можно пре­небречь при условии, что имеется только одна сверхпроводящая область. Если между двумя сверхпроводниками имеется гра­ница (или есть другие обстоятельства, за счет которых r может начать резко меняться), то этот член может стать существенным. Для тех, кто не так уж знаком с уравнениями гидродинамики, я попробую переписать (19.33) в том виде, который позволит яснее видеть физику. Я использую (19.31), чтобы q выразить через v. Беря от всего уравнения (19.33) градиент и выражая с помощью (19.31) Ñq через А и v, я получу

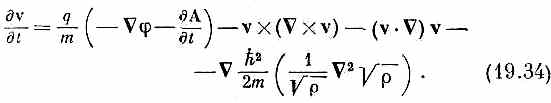
Что же означает это уравнение? Вспомним, во-первых, что

Затем заметим, что если взять ротор от уравнения (19.19), то получится

поскольку ротор градиента всегда нуль. Но ÑX A — это маг­нитное поле В, так что два первых члена можно записать в виде

q/m (E + v X B).

Наконец, вы должны уяснить себе, что дv/дt обозначает ско­рость изменения скорости жидкости в данной точке. Если же вас интересует отдельная частица, то ее ускорение выразится полной производной от v (или, как иногда говорят в динамике жидкостей, «сопутствующим ускорением»), связанной с д v /дt формулой [см. гл. 40, § 2 (вып. 7)]

В правой части (19.34) стоит тот же член (v •Ñ) v. Если перенести его влево, то (19.34) перепишется так:

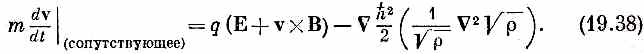
Затем из (19.36) следует

Это и есть уравнения движения сверхпроводящей электрон­ной жидкости. Первое уравнение — это просто закон Ньютона для заряженной жидкости в электромагнитном поле. Оно ут­верждает, что ускорение каждой частицы жидкости с зарядом q вызывается действием обычной лоренцевой силы q (E + v X B) плюс добавочная сила, являющаяся градиентом какого-то таин­ственного квантовомеханического потенциала; эта сила обычно мала и становится заметной только при соприкосновении двух разных сверхпроводников. Второе уравнение утверждает, что жидкость «идеальна» — ротор обладает нулевой дивергенцией (у В дивергенция всегда нуль). Это означает, что скорость может быть выражена через потенциал скоростей. Обычно для идеаль­ной жидкости пишут ÑX v =0, но для идеальной заряженной жид­кости в магнитном поле это уравнение обращается в (19.39).

Итак, уравнение Шредингера для электронных пар в сверх­проводнике дает нам уравнения движения электрически заря­женной идеальной жидкости. Теория сверхпроводимости сов­падает с задачей гидродинамики заряженной жидкости. Если вы хотите решить какую-либо задачу, касающуюся сверхпровод­ников, вы берете эти уравнения для жидкости [или равноценную им пару (19.32) и (19.33)] и сочетаете их с уравнениями Мак­свелла, чтобы получить поля. (Заряды и токи, которыми вы пользуетесь, чтобы узнать поля, должны, естественно, включать как заряды и токи от сверхпроводника, так заряды и токи от внешних источников.)

Кстати, я считаю, что уравнение (19.38) не очень-то правиль­но, в него следует добавить член с плотностью. Он определяется не квантовой механикой, а вытекает из обычной энергии, связан­ной с вариациями плотности, так же как в уравнении для обыч­ной жидкости должна стоять плотность потенциальной энергии, пропорциональная квадрату отклонения r от r₀ (невозмущенной плотности, которая в нашем случае равна также плотности за­ряда кристаллической решетки). Поскольку должны наблюдать­ся силы, пропорциональные градиенту этой энергии, то в (19.38) обязан стоять еще один член, пропорциональный Ñ(r-r₀)². В нашем анализе он не появился, потому что возникает он от взаимодействия между частицами, которым я, применяя прибли­жение независимых частиц, пренебрег. Но это та самая сила, па которую я сослался, когда делал качественное утверждение о том, что электростатические силы стремятся сохранить r вдоль сверхпроводника почти неизменным.

Дата добавления: 2015-06-04