
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Построение регрессивной модели. Метод наимельших квадратов (МНК)
|
|
|
|
Рассмотрим случай 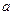 (рис. 4.1,
(рис. 4.1, 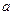 ). Здесь через совокупность точек проведена прямая
). Здесь через совокупность точек проведена прямая 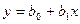 , которая показывает на существованиии зависимости между X и Y. Наша задача в том, чтобы вычислить коэффициенты
, которая показывает на существованиии зависимости между X и Y. Наша задача в том, чтобы вычислить коэффициенты 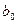 и
и 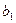 , определяющие положение прямой относительно всех
, определяющие положение прямой относительно всех 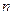 экспериминтальных точек таким образом, чтобы сумма квадратов отклонений между значениями
экспериминтальных точек таким образом, чтобы сумма квадратов отклонений между значениями 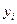 , полученными при эксперименте, и значениями
, полученными при эксперименте, и значениями 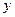 при
при 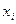 , подставленными в предлагаемое (гипотетическое) уравнение, было минимальным. Для этого используется метод наименьших квадратов (МНК). Пусть разность между экспериментальным
, подставленными в предлагаемое (гипотетическое) уравнение, было минимальным. Для этого используется метод наименьших квадратов (МНК). Пусть разность между экспериментальным 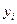 и гипотетическим значением
и гипотетическим значением 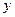 при
при 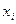 равна
равна  , или
, или 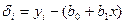 При изменении величин
При изменении величин 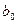 и
и 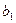 величина
величина  также изменится.Возьмем функцию
также изменится.Возьмем функцию 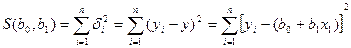 , являющуюся функцией двух переменных
, являющуюся функцией двух переменных 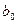 и
и 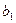 . Наилучшей прямой, описывающей зависимость Yи X для экспериментальных данных,будет такая, где значение
. Наилучшей прямой, описывающей зависимость Yи X для экспериментальных данных,будет такая, где значение  . Для нахождения минимума возьмем частные произвольные от
. Для нахождения минимума возьмем частные произвольные от 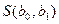 по
по 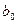 и
и 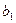 и приравниваем их к нулю:
и приравниваем их к нулю: 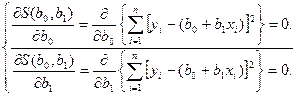 (4.1)
(4.1)
Решая эту систему,называемую системой нормальных уравнений МНК, получим  (4.2)
(4.2)
 (4.3)
(4.3)
Коэффициент b0 есть постояннная уравнения, которая определятся при x=0, a b1 определяет угол наклона прямой регрессии Y к оси OX. В качестве меры зависимости между случайными величинами используется коэффициент корреляции, определяемый по формуле:

 (4.4)
(4.4)
 Коэффициент корреляции всегда находится в пределах от -1 до 1: -1
Коэффициент корреляции всегда находится в пределах от -1 до 1: -1  . Если случайные величины X и Y независимы, то r=0, если связь между Y и X функциональна, то
. Если случайные величины X и Y независимы, то r=0, если связь между Y и X функциональна, то 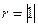 . В качестве меры адекватности регрессионной модели статистическим данным часто используют коэффициент детерминации.
. В качестве меры адекватности регрессионной модели статистическим данным часто используют коэффициент детерминации. 
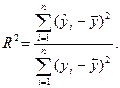 (4.5)
(4.5)
где 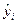 – расчетное (теориетическое) значение величины
– расчетное (теориетическое) значение величины 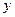 для
для 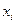 ,вычисленное по уравнению регрессии
,вычисленное по уравнению регрессии  (знак «^» над
(знак «^» над 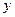 обозначает, что уравнение получено МНК);
обозначает, что уравнение получено МНК);  -среднее значение
-среднее значение 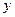 ;
;  ;
; 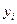 -значение
-значение 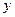 в
в  -м опыте,
-м опыте,  Чем больше значение R2, тем выше степень адекватности уравнения регрессии опытным данным. Для уравнения регрессии вида
Чем больше значение R2, тем выше степень адекватности уравнения регрессии опытным данным. Для уравнения регрессии вида 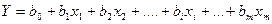 многих переменных
многих переменных  результаты
результаты  -го опыта записываются в виде
-го опыта записываются в виде 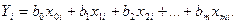 где
где  =1 при всех
=1 при всех 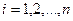 ;
; 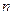 - общее число опытов в эксперименте. Для определения коэффициентов уравнения регрессии
- общее число опытов в эксперименте. Для определения коэффициентов уравнения регрессии  может быть использован МНК, который минимизирует сумму квадратов регрессионых остатков:
может быть использован МНК, который минимизирует сумму квадратов регрессионых остатков:

Если представить результаты эксперимента в матричной форме как Y=XB, где
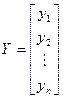 ;
; 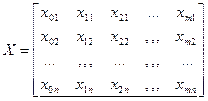 ;
; 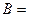
 ,
,
то можно записать:
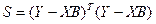 (4.6) (индекс Т означает транспонирование).
(4.6) (индекс Т означает транспонирование).
Исходя их условий минимизации  , (4.7)
, (4.7)
откуда  . (4.8)
. (4.8)
Следовательно, оценка МНК есть такая, при которой коэффициенты уравнения регрессии равны:  . (4.9)
. (4.9)
где индекс -1 означает обратную матрицу.
Коэффициент детерминации (скорректированный)
 . (4.10)
. (4.10)
Оценка меры автокорреляции случайной величины  как правило, производится с помощью статистики Дарбина- Уотсона:
как правило, производится с помощью статистики Дарбина- Уотсона:
 . (4.11) При значении
. (4.11) При значении 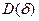 , близком к 2,0, говорят, что автокорреляция отсутствует (что желательно).
, близком к 2,0, говорят, что автокорреляция отсутствует (что желательно).
Пример 4.1. В результате эксперимента зафиксированы пары значений  привеленные в табл. 4.1. Построить уравнение регрессии вида
привеленные в табл. 4.1. Построить уравнение регрессии вида  Таблица 4.1.
Таблица 4.1.
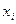
| ||||||||||||||||||

|
Решение. Для вычисления коэффициентов уравнения регрессии составляем статистическую таблицу 4.2. По вычисленным суммам определяем: 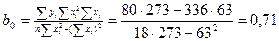 ,
,  тогда уравнение регрессии будет иметь вид
тогда уравнение регрессии будет иметь вид 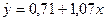 Таблица 4.2.
Таблица 4.2.
| Номер опыта | 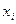
| 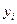
|    
| 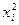
| 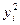
|
| Сумма |
Определим коэффициент корреляции  отсюда следует, что Y и X тесно связаны друг с другом, так как коэффициент корреляции близок к единице.
отсюда следует, что Y и X тесно связаны друг с другом, так как коэффициент корреляции близок к единице.
При нелинейной форме связи могут быть оспользованы два подхода: 1) когда нелинейная форма связи представляется в виде линеаризованной функции; 2) когда используется итерационный нелинейный метод наименьших квадратов. В первом случае исследователь сначала выбирает форму нелинейной связи,затем ее линеаризует, преобразую члены уравнения регрессии,например, как показано в таблице 4.3.
| Функции | Линеаризующие преобразования | |||
| Преобразования переменных | Преобразования коэффициентов | |||

| 
| 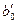
| 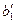
| |

|  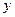
| 
| 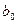
| 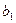
|

| 
| 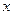
| 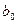
| 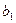
|
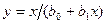
| 
| 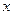
| 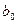
| 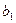
|

| 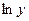
| 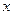
| 
| 
|
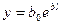
| 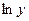
| 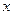
| 
| 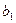 
|

| 
| 
| 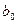
| 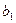
|
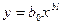
| 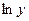
| 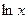
| 
| 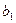
|

| 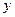
| 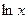
| 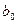
| 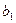
|
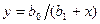
| 
| 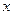
| 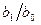
| 
|

| 
| 
| 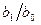
| 
|
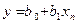
| 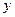
| 
| 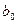
| 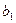
|
Затем используется метод МНК для линеаризованного уравнения, откуда определяются коэффициенты уравнения регрессии. Полученное уравнение затем вновь преобразуется в нелинейную форму.
Пример 4.2. В результате многолетних исследований величины прибыли на рубль затрат (Y) в зависимости от вложенного капитала (X) получены данные:
| Величина вложенного капитала X, млн. руб. | |||||||
| Величина прибыли Y, руб. на 1 руб. затрат | 0,5 | 1,0 | 1,4 | 1,7 | 1,8 | 1,9 | 2,0 |
Найти зависимость между величиной прибыли и величиной вложенного капитала. Решение: предполагаемая зависимость Y от X имеет вид 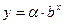
Линеаризуем уравнение при 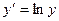 ;
;  ;
; 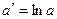 и
и 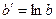 , тогда
, тогда  . Составляем статистическую таблицу:
. Составляем статистическую таблицу:
| x | 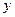
| 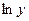
|   
| 
| |
| 0,5 | -0,3010 | -0,3010 | |||
| 1,0 | 0,0000 | 0,0000 | |||
| 1,4 | 0,1461 | 0,4383 | |||

| 0,2304 | 0,9216 | |||
| 1,8 | 0,2553 | 1,2765 | |||
| 1,9 | 0,2788 | 1,6728 | |||
| 2,0 | 0,3010 | 2,1070 | |||

| 10,3 | 0,9106 | 6,1152 | ||
Составляем систему нормальных уравнений МНК:  или
или  Откуда после преобразований получим: a=0,6; b=1,226. Следовательно, уравнение регрессии для зависимости величины прибыли от вложенного капитала будет иметь вид
Откуда после преобразований получим: a=0,6; b=1,226. Следовательно, уравнение регрессии для зависимости величины прибыли от вложенного капитала будет иметь вид 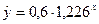 .
.
В таблице 4.4 приведены нормальные уравнения МНК для некоторых функций. Таблица 4.4.
| Функции | Нормальные уравнения |

| 
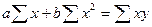
|
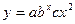
| 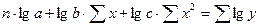


|
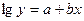
| 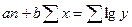

|

| 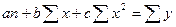
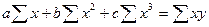

|
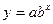
| 
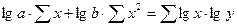
|

| 

|
Рассмотрим второй случай- метод наименьших квадратов для нелинейных форм. Пусть Y-целевая функция, а  набор ее наблюдений;
набор ее наблюдений; 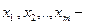 переменные факторы. Наблюдение
переменные факторы. Наблюдение 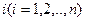 представляет из себя вектор
представляет из себя вектор 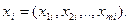 Необходимо целевую функцию Y выразить через вектор X посредством функции
Необходимо целевую функцию Y выразить через вектор X посредством функции 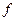 , вид которой известен, однако неизвестны некоторые ее параметры
, вид которой известен, однако неизвестны некоторые ее параметры  Тогда для
Тогда для  можно записать:
можно записать: 
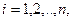 где
где  - отклонение(ошибка). Если исключить параметры
- отклонение(ошибка). Если исключить параметры  , то функция запишется в виде
, то функция запишется в виде 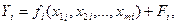 (4.12) в которую входят только те параметры, которые необходимо найти МНК. Минимизируя
(4.12) в которую входят только те параметры, которые необходимо найти МНК. Минимизируя  (4.13) и используя метод Маркварда, введем векторы
(4.13) и используя метод Маркварда, введем векторы  ;
; 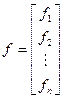 ;
;  ;
;  . Сформулируйте задачу в виде: найти
. Сформулируйте задачу в виде: найти  такое, что при
такое, что при 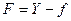 целевая функция (сумма квадратов остатков)
целевая функция (сумма квадратов остатков)  минимизируется. Приближенное значение
минимизируется. Приближенное значение  , получаемое на
, получаемое на  шаге итеративного процесса, и последующее приближенное значение
шаге итеративного процесса, и последующее приближенное значение 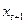 связаны между собой вектором поправки
связаны между собой вектором поправки  т.е.
т.е.  .
.  (4.14) Формула вектора поправки
(4.14) Формула вектора поправки 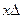 согласно условию минимизации выводится из решения системы линейных уравнений
согласно условию минимизации выводится из решения системы линейных уравнений 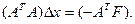 (4.15) откуда
(4.15) откуда 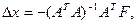 (4.16) где А- первая частная производная от F, определяемая как матрица Якоби:
(4.16) где А- первая частная производная от F, определяемая как матрица Якоби: 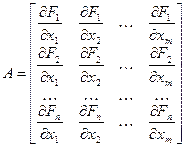 при
при  (4.17) Это формулы итерации по методу Ньютона –Гаусса. Если степень нелинейности
(4.17) Это формулы итерации по методу Ньютона –Гаусса. Если степень нелинейности  высока, а стартовое значение
высока, а стартовое значение  далеко отстоет от минимизирующего значения,то при их использовании велика вероятность «раскачки»
далеко отстоет от минимизирующего значения,то при их использовании велика вероятность «раскачки» 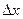 и расходимисти процесса. Левенберг и Марквардт в процедуре Ньютона-Гаусса продложили искать корректирующий вектор
и расходимисти процесса. Левенберг и Марквардт в процедуре Ньютона-Гаусса продложили искать корректирующий вектор 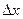 из уравнения
из уравнения 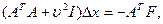 (4.18) где I-еденичная матрица;
(4.18) где I-еденичная матрица; 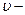 некоторая величина, называемая числом Марквардта. Тогда
некоторая величина, называемая числом Марквардта. Тогда  (4.19) При вычислениях рекомендуется за начальное значение принимать
(4.19) При вычислениях рекомендуется за начальное значение принимать 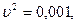 затем на каждом шаге увеличивать
затем на каждом шаге увеличивать  в десять раз, до тех пор,пока S не начнет уменьшаться.
в десять раз, до тех пор,пока S не начнет уменьшаться.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 423; Нарушение авторских прав?; Мы поможем в написании вашей работы!