
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нелинейный регрессионный анализ
|
|
|
|
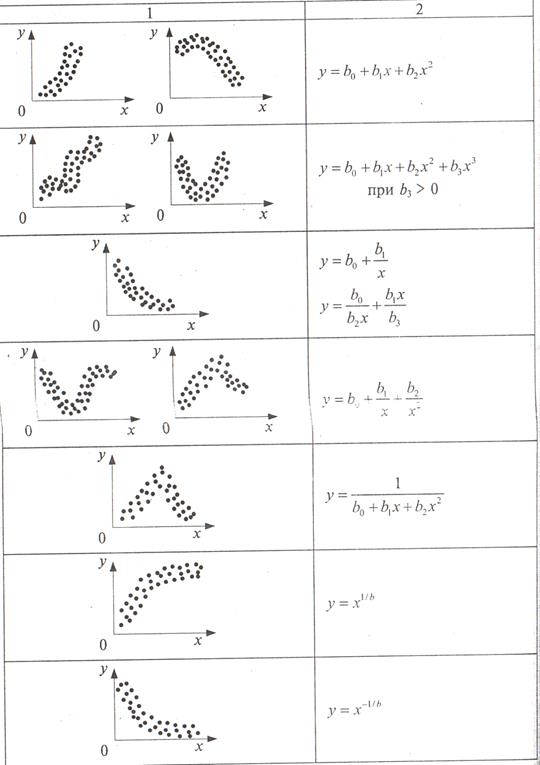
Если при проверке гипотезы о линейности устанавливается, что статистический материал не может быть описан линейным уравнением, то переходят к поиску нелинейной модели. Для предварительного выбора вида модели можно использовать примеры, приведенные в таблице 4.5. Можно воспользоваться интерполяцией, в частности интерполяционной формулой Лагранжа:
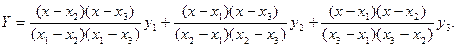 (4.20)
(4.20)
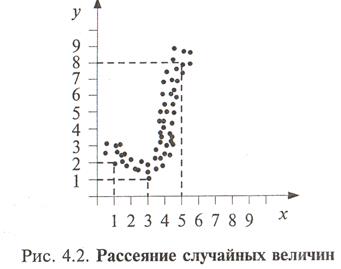
Для этого на поле рассеяния(рис. 4.2) следует выбрать несколько характерных точек, например 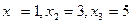 и записать соответствующие пары
и записать соответствующие пары 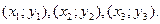
Определение вида функции по виду поля рассеяния.
Таблица 4.5.

Тогда интерполяционная формула Лагранжа при 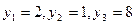 будет иметь вид
будет иметь вид
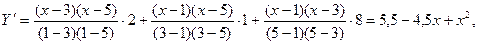
т.е. 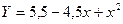 .
.
Для одного и того же статистического материала могут быть использованы различные формы связи. Лучшей моделью следует считать ту, которая дает наименьшее значение остаточной дисперсии
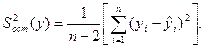 (4.21)
(4.21)
После построения уравнения регрессии по методу наименьших квадратов проводят оценивание значимости коэффициентов уравнения регрессии и коэффициента корреляции, а также значимость уравнения в целом.
Рассмотрим оценивание уравнения регрессии, полученного в примере 4.1. Полученное уравнение
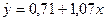
рассматривают по нескольким параметрам.
Статистическое оценивание коэффициентов уравнения регрессии. Для статистического оценивания коэффициентов уравнения регрессии проверяют нулевую гипотезу: 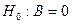 (B- значение коэффициента уравнения регрессии в генеральной совокупности), т.е. проверяют, отличается ли статистически значимо оценка коэффициента регрессии от нуля. Границу значимости устанавливают по критерию Стьюдента
(B- значение коэффициента уравнения регрессии в генеральной совокупности), т.е. проверяют, отличается ли статистически значимо оценка коэффициента регрессии от нуля. Границу значимости устанавливают по критерию Стьюдента
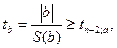 (4.22)
(4.22)
где 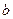 - выборочная оценка коэффициента уравнения регрессии;
- выборочная оценка коэффициента уравнения регрессии;
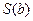 - среднее квадратическое отклонение коэффициента
- среднее квадратическое отклонение коэффициента 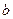 ;
;
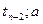 - значение критерия Стьюдента при числе степеней свободы
- значение критерия Стьюдента при числе степеней свободы 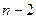 и уровне значимости
и уровне значимости 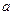 .
.
Если 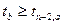 выполняется, по гипотезу
выполняется, по гипотезу 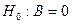 отклоняют, т.е. коэффициент уравнения регрессии значимо отличается от нуля.
отклоняют, т.е. коэффициент уравнения регрессии значимо отличается от нуля.
Пример 4.3. По данным примера 4.1 произвести статистическую оценку коэффициентов уравнения регрессии
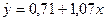
Решение: Вычисляем статистику 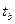 для коэффициентов
для коэффициентов 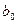 и
и 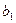 :
:
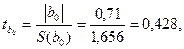
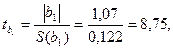
где средние квадратические отклонения вычисляем по формуле:
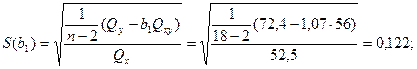
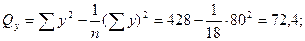
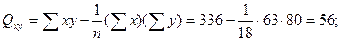
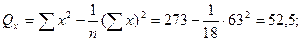
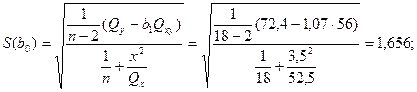
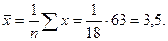
По таблице приложения 7 определяем значение критерия Стьюдента при числе степеней свободы 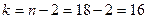 и уровне значимости
и уровне значимости 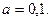 :
:
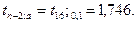
Сравниваем:
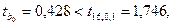
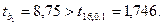
Отсюда делаем заключение, что коэффициент 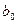 незначим, т.е. принимается гипотеза
незначим, т.е. принимается гипотеза 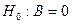 , а коэффициент
, а коэффициент 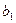 значим, т.е. гипотеза
значим, т.е. гипотеза 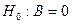 отклоняется. Тогда уравнение из вида
отклоняется. Тогда уравнение из вида 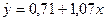 должно быть преобразовано в уравнение
должно быть преобразовано в уравнение 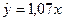 с доверительной вероятностью (надежностью)
с доверительной вероятностью (надежностью) 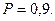
Статистическое оценивание коэффициентов корреляции. Для статистического оценивания коэффициента корреляции проверяют нулевую гипотезу 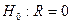 , где R- коэффициент корреляции в генеральной совокупности. Границу значимости устанавливают по критерию Стьюдента.
, где R- коэффициент корреляции в генеральной совокупности. Границу значимости устанавливают по критерию Стьюдента.
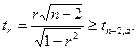 (4.23)
(4.23)
Если это условие выполняется, то гипотезу 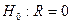 отклоняют, т.е. коэффициент
отклоняют, т.е. коэффициент 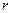 принимается значимым.
принимается значимым.
Пример 4.4. По данным примерам 4.1 определить значимость коэффициента корреляции 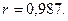
Решение: Вычисляем статистику 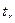 для коэффициента корреляции:
для коэффициента корреляции: 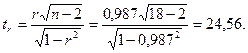
По таблице приложения 7 выбираем значение критерия Стьюдента при уровне значимости 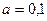 и числе степеней свободы
и числе степеней свободы 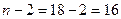 :
:
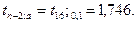
При условии
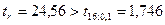
Гипотеза 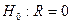 отклоняется, т.е. полученный коэффициент корреляции является значимым.
отклоняется, т.е. полученный коэффициент корреляции является значимым.
Проверка значимости полученного уравнения регрессии. Для проверки значимости полученного уравнения регрессии, т.е. адекватности полученного уравнения результатам эксперимента, используют критерий Фишера
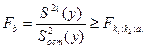 (4.24)
(4.24)
где 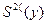 - дисперсия случайной величины
- дисперсия случайной величины  :
:
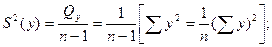 (4.25)
(4.25)
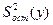 -остаточная дисперсия,
-остаточная дисперсия,
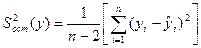 . (4.26)
. (4.26)
Величина 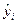 вычисляется для каждого
вычисляется для каждого 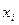 из
из 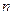 по формуле
по формуле 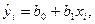 а затем находится разность экспериментального
а затем находится разность экспериментального 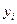 и теоретического
и теоретического 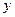 значений по всем
значений по всем 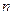 экспериментам.
экспериментам.
Остаточная дисперсия имеет важное значение в статистических исследованиях, так как она представляет собой показатель ошибки предсказания результатов опята уравнением регрессии.
Критерии 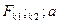 находится по таблице Фишера при заданном уровне значимости
находится по таблице Фишера при заданном уровне значимости 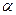
и числе степеней свободы 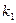 для
для 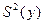 и
и 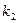 для
для 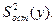 Для
Для 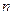 испытаний принимают
испытаний принимают 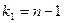 и
и 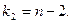
Если условие 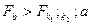 выполняется, то уравнение регрессии адекватно описывает статистические данные, т.е. статистически значимо для полученных в результате эксперимента данных.
выполняется, то уравнение регрессии адекватно описывает статистические данные, т.е. статистически значимо для полученных в результате эксперимента данных.
Пример 4.5. Проверить значимость уравнения регрессии 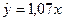
по данным, вычисленным по табл. 4.1, при 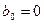 и
и 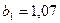 .
.
Решение. Вычисляем 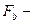 статистику:
статистику:
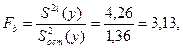
где 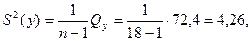
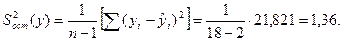
По таблице приложения 8 находим значение критерия Фишера при уровне значимости а = 0,1 и числе степеней свободы 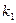 = 18 — 1 = = 17;
= 18 — 1 = = 17; 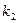 = п- 2 = 18 - 2 = 16:
= п- 2 = 18 - 2 = 16:
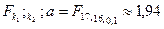
Сравниваем:
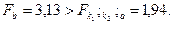
т.е. уравнение регрессии 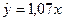 адекватно описывает результаты эксперимента.
адекватно описывает результаты эксперимента.
Проверка линейности уравнения регрессии. Для проверки линейности уравнения регрессии используется следующий подход. Так как изменение функции отклика Y носит случайный характер, то при каждом значении х рекомендуется проводить несколько экспериментов, чтобы для данного значения 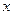 получить некоторое среднее значение
получить некоторое среднее значение 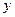 . В этом случае экспериментальный материал табл. 4.1 представляется в виде табл. 4.6. Здесь принимается
. В этом случае экспериментальный материал табл. 4.1 представляется в виде табл. 4.6. Здесь принимается 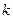 уровней
уровней 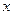 , число значений у для
, число значений у для 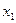 берется равным
берется равным 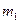 а общее число экспериментов
а общее число экспериментов
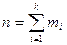 .
.
Значение 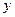 в
в 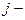 м эксперименте для
м эксперименте для 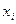 обозначаем как
обозначаем как 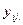 Среднее значение
Среднее значение 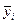 для
для 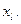
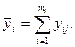
Таблица 4.6.
Уровни значений 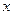
| Полученные значения 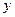 при при 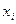
| Число опытов,  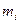
| Среднее значение 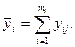
| Сумма квадратов разности 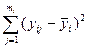
|  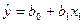 (при (при 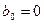 , , 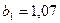 , , 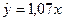  ) )
| 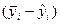
| 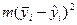
| ||
| Номер опыта | |||||||||
| 2,00 2,67 4,00 5,00 5,33 7,67 | 2,00 1,11 2,00 2,00 2,67 0,33 | 1,070 2,140 3,210 4,280 5,350 6,420 | 0,930 0,530 0,790 0,720 0,020 1,250 | 2,6114 0,8619 1,9052 1,6074 0,0007 4,8234 | |||||
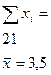
| 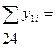
| 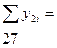
| 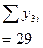
|  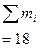
| 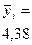
| 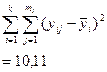
| - | - | 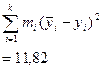
|
Для проверки линейности уравнения регрессии вычисляется 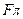
 статистика
статистика
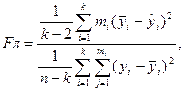 (4.27)
(4.27)
Когда сравнивается с критическим значением критерия Фишера 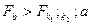 при уровне значимости
при уровне значимости 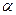 и числе степеней свободы
и числе степеней свободы 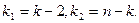
При 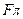 <
< 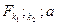 гипотеза о линейности уравнения регрессии принимается, а при
гипотеза о линейности уравнения регрессии принимается, а при 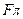 >
> 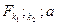 - отвергается. Во втором случае для описания экспериментального материала необходимо выбрать нелинейную модель.
- отвергается. Во втором случае для описания экспериментального материала необходимо выбрать нелинейную модель.
Пример 4.6. По результатам наблюдений, представленным в табл. 4.1, проверить линейность уравнения регрессии 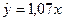 .
.
Решение. Результаты наблюдений, приведенные в примере 4.1, представляем в виде табл. 4.6. Определяем 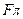 статистику:
статистику:
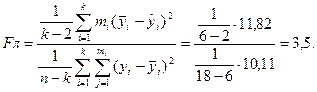
По таблице приложения 10 находим при уровне значимости 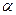 — 0,05 и числе степеней свободы
— 0,05 и числе степеней свободы 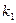 = 6 — 2 = 4,
= 6 — 2 = 4, 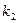 = 18 — 6 = 12:
= 18 — 6 = 12:
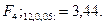
Сравниваем:

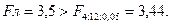
Следовательно, гипотезу о линейности уравнения регрессии 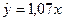 следует отвергнуть и перейти к рассмотрению нелинейной формы связи у с x.
следует отвергнуть и перейти к рассмотрению нелинейной формы связи у с x.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 1204; Нарушение авторских прав?; Мы поможем в написании вашей работы!