Исследование функции и построение ее графика

Исследование функции предполагает изучение ее основных свойств.

1.ООФ. - область определения функции.

ООФ. – множество тех значений аргумента, при которых функция принимает конечные действительные значения. Для элементарных функций в ООФ входят значения независимой переменной, при которых:

· выражение, стоящее в знаменателе, не обращается в нуль;

· под корнем четной степени не возникает отрицательное выражение;

· выражение, стоящее под знаком логарифма, положительное;

· выражение, стоящее под знаком арксинуса или арккосинуса, по модулю не больше единицы.

Если функция f(x) не определена в некоторой точке х₀, то эта точка может быть для данной функции точкой разрыва, т.е. в точке х₀ функция не является непрерывной. Точка х₀ является точкой разрыва функции f(x), если имеет место хотя бы одно из 4-х равенств

(12)

Или хотя бы один из указанных пределов не существует.

2. Вертикальные асимптоты.

Прямая х = х₀ называется вертикальной асимптотой графика функции f(x), если имеет место хотя бы одно из четырех равенств (12).

Чтобы найти вертикальные асимптоты, надо проверить справедливость равенств (12) для граничных точек ООФ, а также для точек, в которых выражение, стоящее в знаменателе, обращается в нуль.

3. Наклонные асимптоты.

Изучая характер поведения функции при , следует установить, имеет ли график наклонную асимптоту. Прямая y=k∙x+b называется наклонной асимптотой графика функции y=f(x), если

.

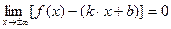Чтобы найти наклонную асимптоту, достаточно вычислить параметр k, а затем параметр b по формулам:

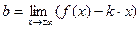
Если хотя бы один из этих пределов равен бесконечности или не существует, то наклонных асимптот нет. Если k =0, то график имеет горизонтальную асимптоту. Заметим, что указанные пределы, вообще говоря, следует вычислять отдельно пр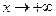и и , т.к. значения пределов в этих двух случаях могут не совпадать.

4. Свойство четности.

Если ООФ симметрична относительно начала координат и для любого значения х из ООФ выполняется равенство f(-x)=f(x), то функция f(x) – четная. Если же выполняется равенство f(-x)=-f(x), то функция f(x) – нечетная. Во всех других случаях говорят, что функция f(x) общего вида. Если функция f(x) обладает свойством четности, то достаточно изучить её свойства и построить график, например, только для значений . Для построения графика при х <0 достаточно отразить построенную часть относительно оси ординат, если f(x) четная, или относительно начала координат, если функция f(x) нечетная.

5.Точки пересечения с осями координат.

Для построения графика функции полезно знать координаты точек пересечения графика с координатными осями. Чтобы найти точки пересечения с осью абсцисс, надо найти корни функции, а значения функции при х =0 определят точку пересечения с осью ординат. И так:

точка пересечения с осью 0 х: f(x₀)=0, (x₀,0);

точка пересечения с осью 0 у: f(0)=у₀, (0, у₀).

6. Интервалы монотонности и точки локального экстремума.

Напомним, что свойства первой производной функции позволяют выяснить свойства монотонности и точки экстремума самой функции. По определению функция называется монотонно возрастающей (убывающей) на данном интервале, если для любых двух значений аргумента из этого интервала большему значению аргумента соответствует большее (меньшее) значение функции. Можно доказать, что если первая производная положительна (отрицательна) во всех точках некоторого промежутка, то функция на этом промежутке возрастает (убывает).

Точка х ₀ называется точкой локального максимума (минимума) непрерывной функции y=f(x), если найдется такая окрестность точки х ₀, принадлежащая ООФ, что для всех точек из этой окрестности, отличных от х ₀, справедливо неравенство, при чём:

если f(x) <f(x₀) то x₀ - max;

если f(x) >f(x₀) то x₀ - min.

Известно, что точка х ₀ является точкой, подозрительной на экстремум (стационарной) точкой для функции f(x), если в этой точке первая производная равна нулю (необходимый признак экстремума). Точкой, подозрительной на экстремум, является также точка разрыва первой производной. Чтобы проверить, является ли подозрительная точка точкой экстремума непрерывной функции, необходимо проверить, выполняется ли достаточное условие экстремума: если справа и слева от точки х ₀, подозрительной на экстремум, первая производная имеет разные знаки, то точка х ₀ - точка экстремума функции.

Итак, для того, чтобы найти интервалы монотонности, следует:

а) вычислить первую производную, найти ее корни и точки разрыва. Эти точки являются подозрительными на экстремум.

б) Отметить на числовой оси точки подозрительные на экстремум и определить интервалы знакопостоянства . На тех промежутках, где > 0, функция возрастает, < 0, - функция убывает.

в) определить точки локального экстремума по следующему признаку: если слева и справа от точки возможного экстремума первая производная имеет разные знаки, то в этой точке функция имеет локальный экстремум.

возр. max убыв. убыв. min возр. поведение y

На рисунке иллюстрируется поведение производной в районе точки экстремума.

Замечания:

а) прежде чем определить корни и точки разрыва , следует сократить дробь на общие множители;

б) если первая производная терпит разрыв в некоторой точке х₀, в которой не существует сама функция, то данная точка не является точкой локального экстремума.

7. Промежутки выпуклости и точки перегиба.

Если функция, например, возрастает на данном интервале, то ее график может быть обращен выпуклостью вверх или вниз. Чтобы определить направление выпуклости и точки перегиба, т.е. такие точки, в которых характер выпуклости меняется, необходимо исследовать свойства второй производной функции.

Свойства второй производной играют в вопросах выпуклости и перегиба такую же роль, что и свойства первой производной в вопросах монотонности и экстремума. Можно доказать, что если вторая производная положительна (отрицательна), во всех точках некоторого промежутка, то график функции на этом промежутке обращен выпуклостью вниз (вверх).

Точка х ₀ является точкой, подозрительной на перегиб для функции у=f(x), если в этой точке вторая производная равна нулю (необходимое условие перегиба). Точка разрыва второй производной тоже является точкой, подозрительной на перегиб. Чтобы выяснить, является ли подозрительная точка точкой перегиба непрерывной функции, необходимо проверить выполнение достаточного условия перегиба: если справа и слева от подозрительной точки х ₀ вторая производная имеет разные знаки, то х ₀ является точкой перегиба.

Чтобы найти интервалы выпуклости и точки перегиба, следует:

· вычислить вторую производную, найти ее корни и точки разрыва, которые являются точками, подозрительными на перегиб;

· определить интервалы знакопостоянства второй производной. На промежутках,

· где >0, график направлен выпуклостью вниз,

· где <0, график направлен выпуклостью вверх;

· определить точки перегиба по правилу: если справа и слева от подозрительной точки вторая производная имеет разные знаки, то такая точка является точкой перегиба графика функции.

Замечания, сделанные в п.6 относительно первой производной, справедливы и относительно второй производной.

8. Составление таблиц.

Результаты исследования удобно оформить в виде таблицы, которая упростит построение графика. В таблицу вносятся:

· точки разрыва функции;

· корни и точки разрыва первой производной;

· корни и точки разрыва второй производной;

· промежутки между точками, отмеченными в предыдущих пунктах.

В таблице указываются знаки и и соответствующее им поведение самой функции.

9. Построение графика.

Начертить асимптоты, отметить координаты точек экстремума, перегиба, точек пересечения с осями координат. Используя внесенные в таблицу результаты исследования функции, построить график.

Пример 8. Исследовать функцию

и построить ее график.

Решение.

1. ООФ

т.е. . (поскольку x+1 0 - x -1, - в точке x=-1 функция не определена!!!).

2. Вертикальные асимптоты.

Вычислим пределы:

; .

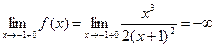Следовательно, график имеет вертикальную асимптоту, заданную уравнением х = -1.

3. Наклонные асимптоты. Вычислим параметры k и b

.

Следовательно, наклонная асимптота существует и имеет уравнение:

.

4. Свойства четности.

Имеем

Из этой записи делаем вывод: рассматриваемая функция не является ни четной, ни нечетной, следовательно, это функция общего вида.

5. Точки пересечения с осями координат.

С осью 0х: поскольку точка пересечения - (.) М (0,0)

С осью 0y: - (.) М (0,0).

6. Интервалы монотонности и точки локального экстремума.

Поскольку

,

то,

корни =0: х = 0, х = -3;

точки разрыва : х = -1.

Точки х =0 и х=-3 являются точками, подозрительными на экстремум. Точка х =-1 не входит в ООФ и, следовательно, не может быть точкой экстремума.

Определим знаки производной на интервале ее знакопостоянства:

знак

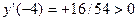
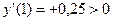
При переходе через точку x=-3 знак первой производной меняется с + на -, следовательно в точке х = -3 исследуемая функция имеет максимум.

7. Промежутки выпуклости и вогнутости, точки перегиба.

Вычислим вторую производную

и найдем ее корни и точки разрыва

корни : х =0;

точки разрыва : х =-1

Точка х =0 является точкой, подозрительной на перегиб. В точке х =-1 перегиба не может быть, так как она не входит в ООФ.

Определим знаки второй производной на интервалах знакопостоянства:

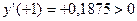
таким образом:

Знак

При переходе через точку х = 0 знак второй производной меняется, следовательно, точка х = 0 – точка перегиба.

8. Построение таблицы.

Сведем результаты проведенного исследования в таблицу:

х	(-∞,-3)	-3	(-3,-1)	-1	(-1,0)		(0,+∞)
	+		-	˟	+		+
		-	-	˟	-		+
у		- 27   max		˟		т.п.

Выпукла вверх выпукла вверх выпукла вверх выпукла вниз

Символом ˟ отмечены точки разрыва функции и производных. Стрелки в нижней строке таблицы отражают характер поведения функции на соответствующих участках: монотонность и направление выпуклости.

9. Построение графика.

Используя сведенные в таблицу результаты исследования функции, убеждаемся, что график исследуемой функции имеет вид

Рис.7

Пример 9. Исследовать функцию

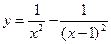, и построить ее график.

1.ООФ

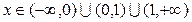, т.е. .

2.Вертикальные асимптоты.

Вычислим пределы

; ;

;

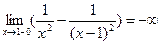
Следовательно, график имеет вертикальные асимптоты, описываемые уравнениями: х =0, х =1

3. Наклонные асимптоты.

Вычислим параметры k и b:

Следовательно, наклонная асимптота существует и имеет уравнение: у =0, т.е. асимптотой служит ось 0х.

4. Свойства четности.

, .

Рассматриваемая функция является функцией общего вида.

5. Точки пересечения с осями координат.

С осью 0 х: . (.)М().

Так как (x=0 не входит в ООФ), то с осью 0 у пересечений нет.

6. Интервалы монотонности и точки локального экстремума.

Поскольку

,

то 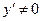, так как квадратный трехчлен (всегда больше нуля) и корней в области действительных чисел не имеет (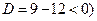. имеет точки разрыва: х =0, х = -1. Итак:

корни : корней нет;

точки разрыва : х =0, х =-1.

Числитель выражения для первой производной положителен при всех значениях х, следовательно, знак определяется знаком знаменателя.

Знак

значения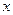

Точек локального экстремума данная функция не имеет, так как 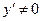, а точки разрыва совпадают с точками разрыва самой функции и не входят в ООФ.

7. Промежутки выпуклости и точки перегиба. Вторая производная имеет вид

.

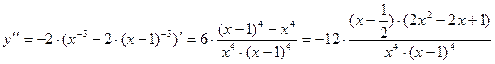Из данного выражения имеем:

корни :

точки разрыва : х=0, х=1.

Других корней не имеет, так как >0 при любых значениях х. Знаки второй производной в исследуемых интервалах приведены ниже.

Значения

Знаки

Точка х=1/2 является точкой перегиба рассматриваемой функции.

8. Построение таблицы.

Сведем результаты проведенного исследования в таблицу.

х	(-∞, 0)		(0, 1/2)	1/2	(1/2, 1)		(1, ∞)
	+	˟	-	-	-	˟	+
	+	˟	+		-	˟	-
у		˟		т.п.		˟

9. Построение графика.

Используя результаты исследования, убеждаемся, что график исследуемой функции имеет вид.

Дата добавления: 2015-06-04