Вычисление площади плоской фигуры

Пусть на плоскости дана геометрическая фигура, ограниченная линией L. Зная уравнение линии в декартовой системе координат, найти площадь фигуры S.

Если фигура представляет собой криволинейную трапецию, образованную графиком функции y=f(x), осью абсцисс и прямыми х = а и х = b, причем 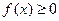на [ a,b ], (a < b), то

.

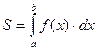Если же график функции y=f(x) расположен ниже оси 0 х, то площадь такой криволинейной трапеции может быть вычислена по формуле

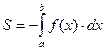
В случае, когда фигура ограничена сверху линией y=f(x), а снизу y=g(x), ее площадь вычисляется по формуле:

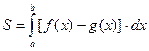
Последняя формула справедлива при любом расположении кривых относительно оси абсцисс (при условии 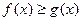для всех ).

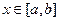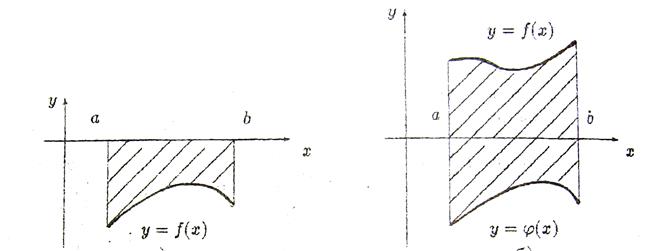
Рис.10

Вычисление площадей более сложных фигур может быть выполнено путем разбиения их на соответствующие части, к которым можно применить одну из приведенных выше формул с последующим суммированием.

Пример 29. Найти площадь криволинейной трапеции, ограниченной параболой

у = 4 х² – 1 и прямыми х = 0, х = 1.

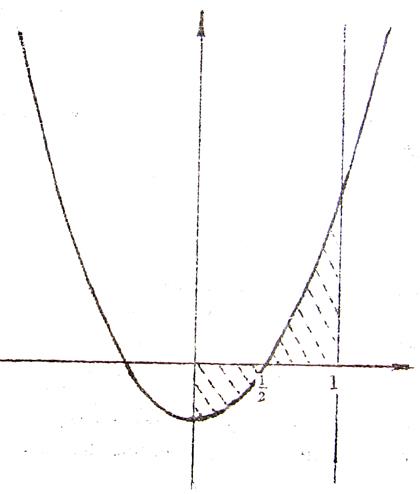
Рис.11

Рассматриваемую фигуру можно представить состоящей из двух частей: криволинейной трапеции D ₁, расположенной ниже оси 0 х на промежутке [0, ½], и криволинейной трапеции D ₂, расположенной выше оси 0 х на промежутке [½, 1].

Тогда получим:

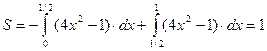
Пример 30.

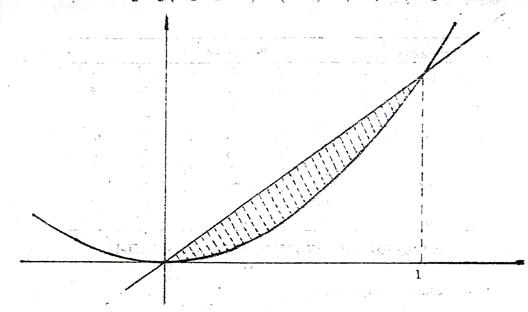
Вычислить площадь фигуры, ограниченной прямой у=х и параболой у = х ².

Найдем абсциссы точек пересечения линий, образующих фигуру

х = х², х - х² = 0, х (1 - х) =0, → х₁= 0, х₂= 1.

.

	у
		х

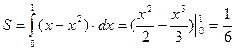Рис. 12

Дата добавления: 2015-06-04