Функции двух переменных. Локальный (безусловный) экстремум

ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Функции одной независимой переменной не охватывают все зависимости, существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести понятие функции нескольких переменных.

Будем рассматривать функции двух переменных, так как все важнейшие факты теории функций нескольких переменных наблюдаются уже на функциях двух переменных. Эти факты обобщаются на случай большего числа переменных. Кроме того, для функций двух переменных можно дать наглядную геометрическую интерпретацию.

Напоминаем, что переменная z называется функцией двух переменных x и у, если каждой паре их значений (х, у) из множества D ставится в соответствие определенное значение z=f(x,y). Множество D называется областью определения функции, а множество всех возможных значений переменной z – областью значений функции.

Геометрически областью определения функции двух переменных является плоскость или часть ее. Например, областью определения функции z = x² +y² является плоскость х 0 у, а для функции z = ln xy область определения первый и третий квадранты плоскости х0у, исключая оси координат, т.е там где ху >0.

Графиком функции двух переменных является поверхность в трехмерном пространстве. Например, графиком функции z=5x+4y-1 является плоскость (5х+4у-z-1=0), а графиком функции - полусфера () радиуса R =5.

Из аналитического задания функции ясно, что данная функция имеет максимум в точке 0(0,0). В общем случае вопрос о существовании и нахождении локального экстремума функции многих переменных, так же как и в случае функции одной переменной, решается методами дифференциального исчисления.

Напомним понятие частных производных функции двух переменных. Пусть дана функция f(x,y). Полным приращением функции f(x,y) в точке М(х,у) называется разность

где - приращения аргументов, вызвавшие данное приращение функции. Если одна из переменных не получает приращения, то соответствующая разность определяет частное приращение по другой переменной

, .

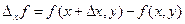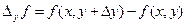Предел отношения частного приращения функции к соответствующему приращению аргумента при стремлении последнего к нулю называется частной производной по данной переменной

.

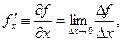
Полный дифференциал функции двух переменных равен сумме частных дифференциалов

Практически при вычислении частных производных руководствуются теми же правилами, что и в случае функции одной переменной, причем, если производная вычисляется по переменной х, то переменная у считается постоянной величиной и наоборот.

Пример 31. найти частные производные и вычислить полный дифференциал функции в точке М (1;4) при dx =0,01; dy =0,02.

Имеем ,

так что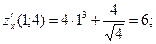

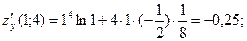
и

Для функции многих переменных, как и в случае одной переменной, вводятся производные старших порядков. Так, для функции двух переменных существуют четыре производные второго порядка:

.

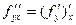Производные и называются смешанными. В нашем курсе будут встречаться только функции, для которых = , хотя для некоторых функций это равенство не справедливо.

Пример 32. Найти все частные производные второго порядка для функции

.

Частные производные первого порядка равны:

, .

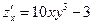Дифференцируя их, получим

, , , .

Напомним определения локального экстремума непрерывной функции двух переменных и методику его нахождения. Точка называется точкой локального максимума (минимума) непрерывной функции f (x,y), если существует такая окрестность точки , принадлежащая ООФ, что для всех точек М(х,у) из этой окрестности, отличных от , выполняется неравенство

, .

Согласно необходимому условию, координаты точки, подозрительной на экстремум (стационарной точки), являются решением системы уравнений

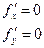
Чтобы выяснить, имеется ли в стационарной точке экстремум и какого типа, необходимо применить достаточное условие экстремума. Составим матрицу из производных второго порядка

.

Вычислим два ее угловых минора в стационарной точке .

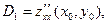
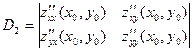
Тогда, если D₂ <0, то в точке экстремума нет, если D₂ >0, то в точке экстремум имеется, причем, если D₁ <0, то максимум, если D₁ >0, то минимум.

Пример 33. Найти экстремум функции z=2x³-xy²+5x²+y²

(I) Используя необходимые условия экстремума, составим систему уравнений и решим ее.

.

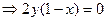Следовательно, возможны два случая:

а) у = 0. Тогда из первого уравнения системы имеем

6 х²+ 10 х= 0, 2 х (3 х+ 5) = 0, х= 0, х=- 5/3,

что дает координаты двух стационарных точек М₁(0,0); М₂(-5/3,0).

б) х = 1. В этом случае из первого уравнения системы получим

16 - у² =0, у = ±4.

В результате имеем координаты еще двух точек, подозрительных на экстремум: М₃ (1,4); М₂ (1,-4).

(II) Проверим выполнение достаточного условия экстремума. Построим матрицу

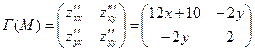
Вычислим значения ее угловых миноров в точке М₁

,
Следовательно, точка М₁ (0,0) является точкой минимума .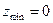

Легко проверить, что в остальных стационарных точках экстремума нет. Например, в точке М₂ имеем:

.

Поскольку D₂ <0, то экстремумов нет.

Дата добавления: 2015-06-04