Однородные дифференциальные уравнения

Уравнения с разделяющимися переменными

Наиболее простым ДУ первого порядка является, уравнение вида

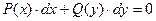. (4.5)

Внем одно слагаемое зависит только от x, а другое - от у. Иногда такие ДУ называют уравнениями с разделенными переменными. Проинтегрировав почленно это уравнение, получаем:

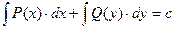- его общий интеграл.

Пример 4.2. Найти общий интеграл уравнения х × dx + у × dy = 0.

Решение: Данное уравнение есть ДУ с разделенными переменными.

Поэтому 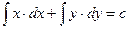или 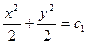Обозначим .

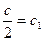Тогда 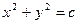- общий интеграл ДУ.

Более общий случай описывают уравнения с разделяющимися переменными, которые имеют вид:

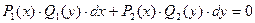(4.6)

Особенность уравнения (4.6) в том, что коэффициенты при dx и dy представляют собой произведения двух функций (чисел), одна из которых зависит только от х, другая - только от у.

Уравнение (4.6) легко сводится к уравнению (4.5) путем почленного деления его на 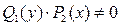. Получаем:

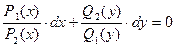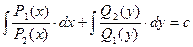, - общий интеграл.

Замечания.

1. При проведении почленного деления ДУ на 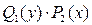могут быть потеряны некоторые решения. Поэтому следует отдельно решить уравнение 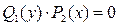и установить те решения ДУ, которые не могут быть получены из общего решения, - особые решения.

2. Уравнение 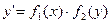также сводится к уравнению с разделенными переменными. Для этого достаточно положить и разделить переменные.

3. Уравнение 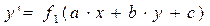, где a, b, c - числа, путем замены

ах + by + с = и сводится к ДУ с разделяющимися переменными. Дифференцируя по х, получаем:

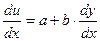, т.е. 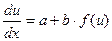, откуда следует .

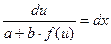Интегрируя это уравнение и заменяя и на ах + by + с, получим общий интеграл исходного уравнения.

Пример 4.3. Решить уравнение (у + ху) dx + (х — ху) dy = 0.

Решение: Преобразуем левую часть уравнения:

.

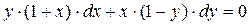Оно имеет вид (4.6). Делим обе части уравнения на :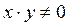

.

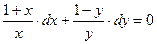Решением его является общий интеграл

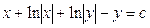, т.е. .

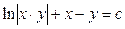Здесь уравнение 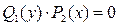имеет вид 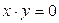. Его решения х = 0, у = 0 являются решениями данного ДУ, но не входят в общий интеграл.

Значит, решения х = 0, у = 0 являются особыми.

Пример 4.4. Решить уравнение 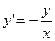, удовлетворяющее условию .

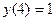Решение:

Имеем: 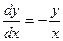или 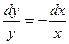. Проинтегрировав, получим:

,

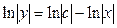т. е. 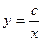общее решение ДУ.

Оно представляет собой, геометрически, семейство равносторонних гипербол. Выделим среди них одну, проходящую через точку (4; 1). Подставим х = 4 и y = 1 в общее решение уравнения: 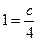, - с = 4.

Получаем: 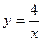- частное решение уравнения .

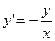Пример 4.5. Найти общее решение ДУ 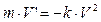, - замедленное движение точки.

Решение: Приведем данное уравнение к виду (4.5):

, , .

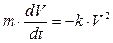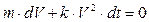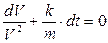Интегрируем: 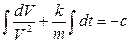, т.е. .

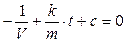Отсюда 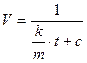- общее решение уравнения.

К уравнению с разделяющимися переменными приводятся однородные ДУ первого порядка.

Функция f(x;y) называется однородной функцией п-го порядка (измерения), если при умножении каждого ее аргумента на произвольный множитель 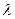вся функция умножится на 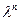, т. е.

.

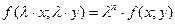Например, функция 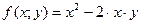- есть однородная функция второго порядка, поскольку

.

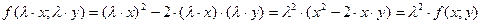Дифференциальное уравнение

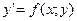(4.7)

называется однородным, если функция f(x;y) есть однородная функция нулевого порядка.

Покажем, что однородное ДУ (4.7) можно записать в виде

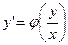. (4.8)

Если 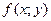- однородная функция нулевого порядка, то, по определению, 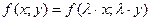. Положив 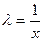, получаем:

.

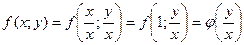Однородное уравнение (4.8) преобразуется в уравнение с разделяющимися переменными при помощи замены переменной (подстановки)

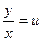или, что то же самое, 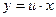. (4.9)

Действительно, подставив 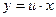и 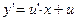в уравнение (4.8), получаем 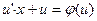или 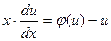, т. е. уравнение с разделяющимися переменными. Найдя его общее решение (или общий интеграл), следует заменить в нем 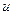на 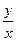. Получим общее решение (интеграл) исходного уравнения.

Однородное уравнение часто задается в дифференциальной форме:

P(x;y)∙dx + Q(x;y)∙dy = 0. (4.10)

ДУ (4.10) будет однородным, если Р(х; у) и Q(x; у) - однородные функции одинакового порядка.

Переписав уравнение (4.10) в виде 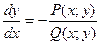и применив в правой части рассмотренное выше преобразование, получим уравнение .

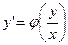При интегрировании уравнений вида (4.10) нет необходимости предварительно приводить их (но можно) к виду (4.8): подстановка (4.9) сразу преобразует уравнение (4.10) в уравнение с разделяющимися переменными.

Пример 4.6. Найти общий интеграл уравнения .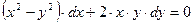

Решение: Данное уравнение однородное, т. к. функции Р(х; у) = 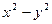и Q(x;y) = 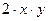однородные функции второго порядка.

Положим 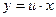. Тогда 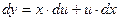. Подставляем в исходное уравнение:

,

,

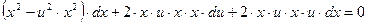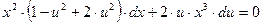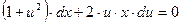
последнее - уравнение с разделяющимися переменными. Делим переменные:

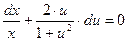
и интегрируем:

, , .

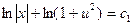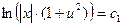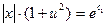Обозначим: 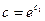, 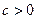. Тогда: .

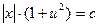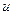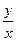Заменяя на , получаем: х² + у² = 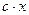- общий интеграл исходного уравнения.

Отметим, что данное уравнение можно было сначала привести к виду (4.8):

, , .

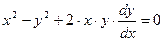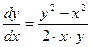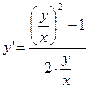Затем положить 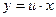, тогда 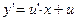и т.д.

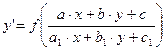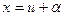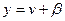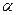Замечание. Уравнение вида , где a, b, c, a₁, b₁, c₁ - числа, приводится к однородному или с разделяющимися переменными. Для этого вводят новые переменные u и v, положив , где и 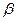- числа. Их подбирают так, чтобы уравнение стало однородным.

Пример 4.7. Найти общий интеграл уравнения

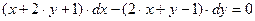, т.е. .

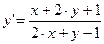Решение: Положив 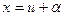, , 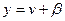получаем:

, ;

.

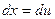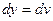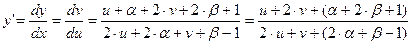Подберем 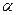и 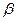так, чтобы

,

.

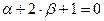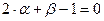Находим: 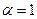, 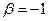. В этом случае заданное уравнение примет вид:

и будет являться однородным. Его решение получается, как это было показано выше, при помощи подстановки v = t·u. Заметим, что, решив его, следует заменить и и v соответственно на 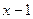и 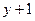. В итоге получим 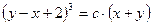- общий интеграл данного уравнения.

Дата добавления: 2015-06-04