Основные способы и методы интегрирования

Основные свойства неопределенного интеграла.

1. Производная неопределенного интеграла равна подынтегральной функции, а дифференциал неопределенного интеграла равен подынтегральному выражению.

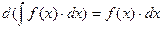
2. Интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной

3. Постоянный множитель можно выносить за знак неопределенного интеграла:

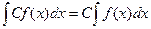, где С - const.

4. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от каждой функции:

.

Поскольку интегрирование является действием, обратным дифференцированию, то таблица основных интегралов может быть получена из таблицы производных основных элементарных функций.

Таблица основных интегралов

1.

2. .

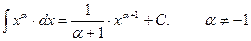3.

4.

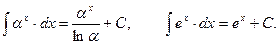
5.

6.

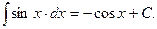
7.

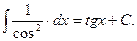
8.

9.

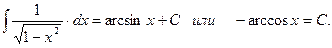
10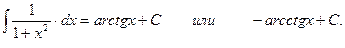

Процесс интегрирования функций состоит в приведении подынтегрального выражения к виду, позволяющему использовать известные формулы интегрирования, например, таблицу основных интегралов. Однако, не существует общих рекомендаций, позволяющих выполнить подобные преобразования. По этой причине задача интегрирования функции оказывается значительно более сложной по сравнению с задачей дифференцирования.

Приведем несколько наиболее общих способов интегрирования.

1. Непосредственное интегрирование.

Пример 14.

Пример 15.

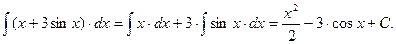
Пример 16.

Пример 17.

Следует отметить, что, так как интегрирование является действием, обратным дифференцированию, то правильность результата можно проверить дифференцированием: производная полученной функции должна быть равна исходной подынтегральной функции. Так, например, дифференцируя функцию убеждаемся, что она является первообразной для функции х +1.

Метод замены переменной (метод подстановки).

Сущность метода состоит в замене переменной интегрирования х на подходящую дифференцируемую функцию 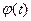. При этом имеет место равенство

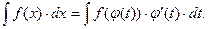(13)

Отметим, что применяя метод подстановки, часто бывает удобно новую переменную t рассматривать как функцию исходной переменной х, то есть вводить замену t=g(x), что и будет использовано в примерах, рассмотренных ниже.

Пример 18.

Сделаем следующую замену переменной: t=x². Вычислим дифференциалы от обеих частей равенства: 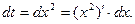Тогда dt = 2x*dx, x*dx = . Следовательно,

Возвращаясь к исходной переменной х, получим

.

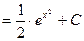Пример 19.

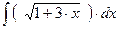
Введем новую переменную t= 1 + 3∙ x. Поскольку dt= 3∙ dx, то

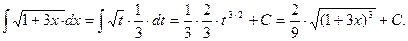
Пример 20.

Для примера 14 используем метод замены переменной

Отличие от результата решения в примере 14 представляется ½, что является константой, и, следовательно, является допустимым отличием. Тем самым мы продемонстрировали использование нескольких методов при выполнении процедуры интегрирования одной и той же функции, что подтверждает выражение «процесс интегрирования – это искусство».

3. Метод интегрирования по частям.

Этот метод является следствием правила дифференцирования произведения U(x) и V(x). Формула интегрирования по частям имеет вид

(14)

Сущность метода состоит в том, что выражение f(x)∙dx, стоящее под знаком интеграла, представляется в виде произведения U(x)∙dV(x), где U(x) и V(х) являются функциями от х и вычисление интеграла сводится к вычислению интеграла 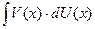. Функции U(x) и V(x) выбираются таким образом, чтобы интегрирование выражения V(x)∙dU(x) было проще, чем интегрирование исходного выражения U(x)∙dV(x). Очевидно, что эффективность применения рассматриваемого метода зависит от того, насколько удачно выбраны функции U(x) и V(х).

Перечислим некоторые типы примеров, в которых следует применить метод интегрирования по частям, и укажем, как выбирать в этих случаях U(x) и V(х).

;

;

,

Здесь 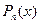-многочлен от переменной х.

Кроме того, метод интегрирования по частям также эффективен в случаях, когда подынтегральная функция содержит в качестве сомножителя логарифм или обратную тригонометрическую функцию, которые и следует принять за U(x).

Пример 21.

Положим U(x)=x+1, dV(x)=e^x∙dx

Тогда

Формула (14) справедлива при любых значениях С, поэтому удобно положить в последнем выражении С =0, Тогда V(x)=e^x.

Применяя формулу интегрирования по частям, получим

Пример 22.

Вычислить .

Положим .

Тогда .

Следовательно, получим

Применим теперь к интегралу в правой части подстановку t=1+x², dt=2x∙dx. Тогда

Следовательно,

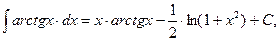
где С = -С₁.

Дата добавления: 2015-06-04