
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Застосування теореми лишків до обчислення визначених інтегралів
|
|
|
|
Основна теорема теорії лишків
Теорема. Нехай  аналітична функція в замкненій області
аналітична функція в замкненій області 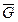 за виключенням скінченого числа ізольованих особливих точок
за виключенням скінченого числа ізольованих особливих точок  , що лежать в середині
, що лежать в середині 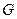 , тоді
, тоді
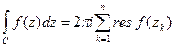 ,
,
де С- повна границя області 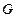 , що проходить в додатному напрямі.
, що проходить в додатному напрямі.
Доведення теореми див. [2, с.305], [1, с.122].
Приклад. 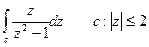 .
.
Оскільки 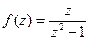 має дві особливі ізольовані точки
має дві особливі ізольовані точки 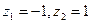 , що лежать в середині контуру С, то
, що лежать в середині контуру С, то

Таким чином,  .
.
Вправи.
Обчислити:

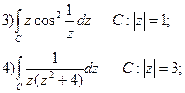
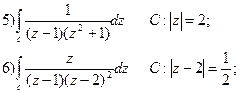


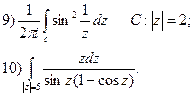 |
Розглянемо  ,
,
де R- раціональна функція своїх аргументів, тоді вірна формула:
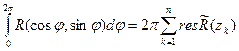 дійсно після заміни
дійсно після заміни 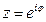 .
.

де 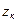 - особлива точка
- особлива точка 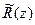 , що міститься в середині
, що міститься в середині 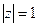 .
.
Приклад. 
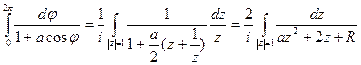
Особливі точки функції
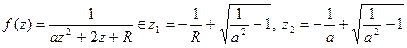 .
.
Точки 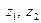 - полюси першого порядку, але в середині
- полюси першого порядку, але в середині 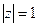 знаходиться тільки точка
знаходиться тільки точка 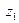 . Тому
. Тому 
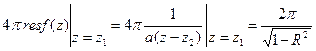
Теорема. Нехай функція  задана на всій дійсній осі
задана на всій дійсній осі 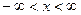 , може бути аналітично продовжена на верхню півплощину
, може бути аналітично продовжена на верхню півплощину 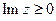 , причому її аналітичне продовження,
, причому її аналітичне продовження,  , задовольняє умовам:
, задовольняє умовам:
1) Існують числа  , для всіх z з верхньої півплощини таких, що
, для всіх z з верхньої півплощини таких, що  виконується оцінка
виконується оцінка 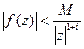 ;
;
2)  не має особливих точок на дійсній осі, а в півплощині
не має особливих точок на дійсній осі, а в півплощині 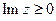 має не більше скінченого числа ізольованих особливих точок.
має не більше скінченого числа ізольованих особливих точок.
Тоді  , де
, де 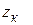 - особлива точка
- особлива точка  в верхній півплощині.
в верхній півплощині.
Доведення теореми див. [1, с. 127].
Приклад. 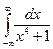 . Тоді
. Тоді  - задовольняє умовам теореми. Особливі точки в верхній півплощині
- задовольняє умовам теореми. Особливі точки в верхній півплощині 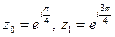 причому обидві – полюси першого порядку. Тому
причому обидві – полюси першого порядку. Тому 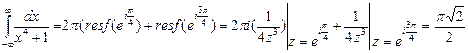 Вправи.
Вправи.
Обчислити.
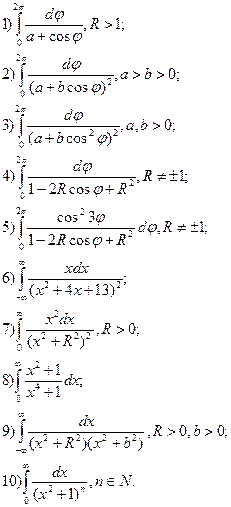
ЗРАЗКИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ З ТЕОРІЇ ФУНКЦІЙ КОМПЛЕКСНОЇ ЗМІННОЇ
Задача № 1. Знайти всі значення 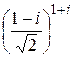 , їх модуль та аргумент.
, їх модуль та аргумент.
Розв'язання. Означення комплексного степеня:  (*), де а
(*), де а  0 і b — довільні комплексні числа.
0 і b — довільні комплексні числа.
Звертаємо увагу на те, що  у правій частині (*) визначено незалежно від вищенаведеного означення степеня (інакше був би «круг в означенні»). А саме:
у правій частині (*) визначено незалежно від вищенаведеного означення степеня (інакше був би «круг в означенні»). А саме:  є значення показникової функції
є значення показникової функції  при
при 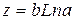 , яка означена як сума степеневого ряду
, яка означена як сума степеневого ряду 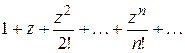 в який входять лише цілі невід'ємні степені z (дія множення). У даному випадку
в який входять лише цілі невід'ємні степені z (дія множення). У даному випадку 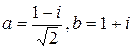 .
.
Маємо за означенням (*) і далі за означенням комплексного логарифма:
 (**)
(**)
Застосувавши до першого множника в (**) формулу Ейлера, матимемо:
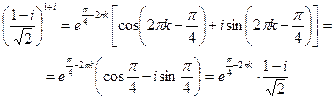 .
.
Порівнюючи (**) з загальною показниковою формою комплексного числа 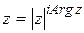 , одержимо:
, одержимо:

Задача № 2. Перевірити умови Даламбера — Ейлера для функції 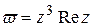 і визначити, в яких точках до є диференційовна функція.
і визначити, в яких точках до є диференційовна функція.
Розв'язання. Хай 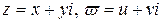 . Тоді рівняння Даламбера — Ейлера мають вигляд:
. Тоді рівняння Даламбера — Ейлера мають вигляд:
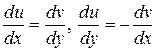 .
.
Відокремимо дійсну і уявну частини функції до:
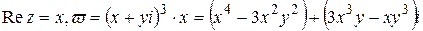 .
.
Отже,
 .
.
Рівності
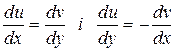 (*)
(*)
очевидно виконуються в точці  . Зовсім легко переконатись, що ця точка є єдиною, в якій задовольняються рівняння Даламбера — Ейлера.
. Зовсім легко переконатись, що ця точка є єдиною, в якій задовольняються рівняння Даламбера — Ейлера.
Справді, перше рівняння системи (*): 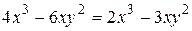 при
при 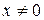 рівносильне рівнянню
рівносильне рівнянню 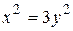 , друге рівняння (*) при
, друге рівняння (*) при 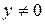 рівносильне рівнянню
рівносильне рівнянню  . А система х2=Зу2, Зх2=у2 не має жодного розв'язку, крім х=0, у=0.
. А система х2=Зу2, Зх2=у2 не має жодного розв'язку, крім х=0, у=0.
Беручи до уваги, що функції u і v є всюди диференційовними, приходимо до висновку, що функція до є диференційовна в точці  (достатність умов Даламбера — Ейлера для диференційовності функції) і лише в цій точці (необхідність цих же умов).
(достатність умов Даламбера — Ейлера для диференційовності функції) і лише в цій точці (необхідність цих же умов).
Задача № 3. Знайти аналітичну функцію 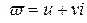 аргумента
аргумента 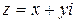 , уявна частина якої
, уявна частина якої  (1)
(1)
Розв'язання. Оскільки 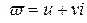 є функція аналітична, для неї справджуються рівняння Даламбера — Ейлера, тобто:
є функція аналітична, для неї справджуються рівняння Даламбера — Ейлера, тобто:
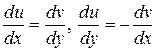
Залишається з цих рівнянь визначити и. Скористаємось першим рівнянням Даламбера — Ейлера. Беручи до уваги (1), маємо:
 ;
;
Звідси 
(тут замість сталої С при знаходженні первісної функції и пишемо 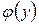 , оскільки у при знаходженні похідної
, оскільки у при знаходженні похідної 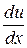 і обчисленні інтеграла вважається за сталу, отже, взагалі кажучи, входить в С).
і обчисленні інтеграла вважається за сталу, отже, взагалі кажучи, входить в С).
Далі, інтегруючи, одержуємо:
 (2)
(2)
Використаємо тепер друге рівняння Даламбера — Ейлера для знаходження 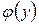 .
.
Для цього спочатку знайдемо  з (2) і
з (2) і 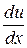 з (1).
з (1).
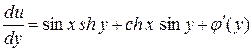 ;
; 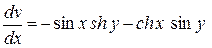
Але 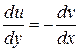 , тобто:
, тобто:
 ;
;
Звідки 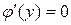 ,
,  ;
;
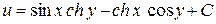 (С — дійсна довільна стала).
(С — дійсна довільна стала).
Отже, 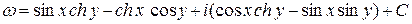 (3)
(3)
Виразимо тепер праву частину (3) через z. Оскільки, дістаємо:
 .
.
Задача № 4. Визначити область збіжності функціонального ряду
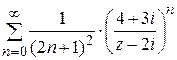
Розв'язання. Застосуємо ознаку збіжності рядів Даламбера, яка, як відомо, має силу і в комплексній області звичайно для ряду модулів.
Маємо:
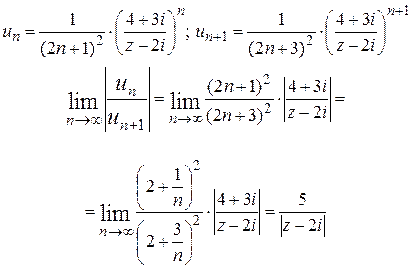
Отже, за ознакою Даламбера ряд буде збіжним (і до того абсолютно) при всіх z таких, що  ;
;
Тобто 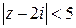 .
.
Якщо 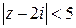 , то
, то 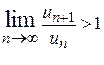 ,
,
Звідки  , і даний ряд буде розбіжним, оскільки не виконується навіть необхідна умова збіжності.
, і даний ряд буде розбіжним, оскільки не виконується навіть необхідна умова збіжності.
Залишається дослідити збіжність ряду при  . При цій умові маємо
. При цій умові маємо 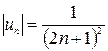 . Ряд
. Ряд  , як легко встановлюється за інтегральною ознакою збіжності, є збіжний. Справді, невласний інтеграл
, як легко встановлюється за інтегральною ознакою збіжності, є збіжний. Справді, невласний інтеграл 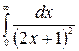 існує:
існує:
 .
.
| 2х + |
Таким чином, область абсолютної збіжності заданого ряду є вся зовнішність круга з центром в точці 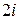 і радіусом, рівним 5, причому коло цього круга включається в область збіжності.
і радіусом, рівним 5, причому коло цього круга включається в область збіжності.
Задача № 5. Розкласти в ряд Тейлора за степенями  функцію
функцію  і визначити радіус збіжності.
і визначити радіус збіжності.
Розв'язання. Функція  є аналітична в усій комплексній площині, за винятком точки
є аналітична в усій комплексній площині, за винятком точки  , отже, її можна розкласти в ряд Тейлора в крузі з центром
, отже, її можна розкласти в ряд Тейлора в крузі з центром  і радіусом, рівним віддалі від точки
і радіусом, рівним віддалі від точки  до найближчої особливої точки:
до найближчої особливої точки:  , звідси радіус круга збіжності з центром в точці
, звідси радіус круга збіжності з центром в точці  є рівний 2. Безпосередній розклад
є рівний 2. Безпосередній розклад  в ряд Тейлора по формулі:
в ряд Тейлора по формулі:

веде до складних обчислень. Використаємо інший спосіб:
 . (*)
. (*)
Представимо  як суму спадної геометричної прогресії:
як суму спадної геометричної прогресії:

Отже,
 при
при 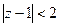 .
.
Що ж до другого доданка (*)  , то він являє собою похідну по z від
, то він являє собою похідну по z від  .
.
Аналогічно попередньому розкладемо  в ряд Тейлора за степенями
в ряд Тейлора за степенями  і про диференціюємо цей степеневий ряд почленно (адже степеневі ряди почленно диференціювати в крузі збіжності):
і про диференціюємо цей степеневий ряд почленно (адже степеневі ряди почленно диференціювати в крузі збіжності):

При 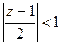 .
.
Нарешті:

В крузі 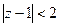 .
.
З теореми єдиності розкладу функції в ряд Тейлора випливає, що одержаний степеневий ряд і є рядом Тейлора функції;
 в крузі
в крузі 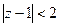 .
.
 Задача № 6. Обчислити інтеграл
Задача № 6. Обчислити інтеграл  , де С —границя півкільця, обмеженого верхніми півколами |z|=1, |z|=2 і відрізками осі абсцис від точки —2 до точки —1, та від точки 1 до точки 2.
, де С —границя півкільця, обмеженого верхніми півколами |z|=1, |z|=2 і відрізками осі абсцис від точки —2 до точки —1, та від точки 1 до точки 2.
Інтегрування проводиться в додатному напрямі (див. рис. 3).
Розв’язання. Перетворимо підінтегральний вираз, помноживши чисельник і знаменник на z:
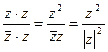 .
.
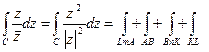 .
.
На колі я  маємо:
маємо:  , аналогічно на другому колі
, аналогічно на другому колі 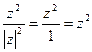
Отже, 
Оскільки підінтегральна функція  є аналітична в будь-якій області, останній інтеграл можна обчислити за формулою Ньютона—Лейбніца:
є аналітична в будь-якій області, останній інтеграл можна обчислити за формулою Ньютона—Лейбніца:

Аналогічно,
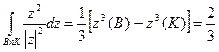
Далі на відрізку АВ  , оскільки тут z є дійсним від'ємним числом, а на відрізку KL
, оскільки тут z є дійсним від'ємним числом, а на відрізку KL  . В обох випадках
. В обох випадках 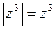 , тому
, тому
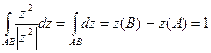 і
і 
Остаточно: 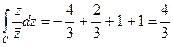
Задача № 7. Обчислити за допомогою інтегральної формули Коші інтеграл 
Розв'язання. Підінтегральна функція є аналітична в крузі  , крім точки
, крім точки  , бо всі інші нулі знаменника: —1, і, —і знаходяться поза цим кругом.
, бо всі інші нулі знаменника: —1, і, —і знаходяться поза цим кругом.
Справді, визначимо віддаль між центром круга а та точкою і, тобто  . Маємо
. Маємо 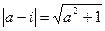 (адже а — дійсне число). Крім цього,
(адже а — дійсне число). Крім цього, 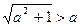 , тобто
, тобто 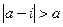 , чим і встановлено, що точка і знаходиться поза колом
, чим і встановлено, що точка і знаходиться поза колом  . Далі
. Далі  ;
;  , отже, точки —і та —1 теж знаходяться поза даним колом.
, отже, точки —і та —1 теж знаходяться поза даним колом.
Представимо тепер розглядуваний інтеграл у вигляді 
Оскільки функція 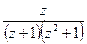 аналітична всередині С і на самому колі С, то можна до інтеграла (*) застосувати інтегральну формулу Коші:
аналітична всередині С і на самому колі С, то можна до інтеграла (*) застосувати інтегральну формулу Коші:
де за  приймемо
приймемо 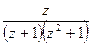 , а за
, а за 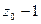 .
.
Тоді 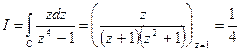 .
.
Задача № 8. Розкласти в ряд Лорана в околі точки  функцію
функцію 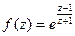 .
.
Розв'язання. Функція  не є аналітичною в точці
не є аналітичною в точці  , отже, вона не розкладається в околі цієї точки в ряд Тейлора. Але цю функцію можна розкласти в околі точки в ряд Лорана, тобто в «двосторонній степеневий» ряд. за степенями
, отже, вона не розкладається в околі цієї точки в ряд Тейлора. Але цю функцію можна розкласти в околі точки в ряд Лорана, тобто в «двосторонній степеневий» ряд. за степенями 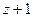 , оскільки область, в якій вона є аналітична (вся комплексна площина з вилученою точкою
, оскільки область, в якій вона є аналітична (вся комплексна площина з вилученою точкою  ), можна розглядати як кругове кільце з центром в точці
), можна розглядати як кругове кільце з центром в точці  , де внутрішній радіус
, де внутрішній радіус 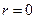 , зовнішній —
, зовнішній — 
Щоб розкласти функцію  в ряд Лорана за степенями
в ряд Лорана за степенями 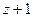 , спочатку перетворимо її тотожно:
, спочатку перетворимо її тотожно:
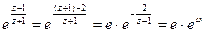 , де
, де  .
.
Використаємо відомий ряд для  :
:
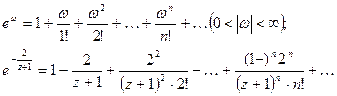
| Є' |
Нарешті: 
Цей розклад справедливий в усій комплексній площині, з якої вилучена точка  .
.
Задача № 9. Розкласти в ряд Лорана функцію  в околі нескінченно віддаленої точки.
в околі нескінченно віддаленої точки.
Розв'язання. Покладемо  ; тоді
; тоді  функцію
функцію  розкладемо в ряд Тейлора в околі точки
розкладемо в ряд Тейлора в околі точки 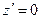 . Для цього розкладемо
. Для цього розкладемо  на елементарні дроби:
на елементарні дроби: 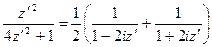 .
.
Кожний із доданків у виразі в дужках представимо як суму спадної геометричної прогресії, а саме:
| 1 — 2/2 |
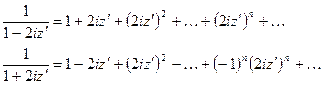
причому обидва розклади мають місце при  (інакше прогресії не будуть спадними). Таким чином:
(інакше прогресії не будуть спадними). Таким чином:

причому цей розклад справедливий у зовнішності круга 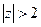 (адже
(адже  і
і  ).
).
Задача № 10. Обчислити за допомогою теореми про лишки інтеграл 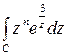 , де С- коло
, де С- коло 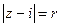 , n – ціле число.
, n – ціле число.
Розв'язання. Контур інтегрування С є коло з центром в точці 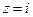 та радіусом r. Якщо
та радіусом r. Якщо 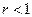 , то функція
, то функція 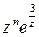 є аналітична в області, обмеженій контуром С, і на самому контурі, оскільки точка
є аналітична в області, обмеженій контуром С, і на самому контурі, оскільки точка 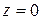 знаходиться поза контуром. Отже, за теоремою Коші — Гурса
знаходиться поза контуром. Отже, за теоремою Коші — Гурса  .
.
Якщо  , то точка
, то точка 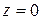 , яка є єдиною особливою точкою підінтегральної функції, знаходиться в області, обмеженій контуром С. Тоді за основною теоремою про лишки
, яка є єдиною особливою точкою підінтегральної функції, знаходиться в області, обмеженій контуром С. Тоді за основною теоремою про лишки 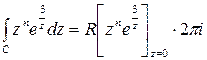
Обчислимо лишок підінтегральної функції в точці 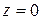 . Для цього розкладемо її в ряд Лорана в околі цієї точки. Маємо:
. Для цього розкладемо її в ряд Лорана в околі цієї точки. Маємо:
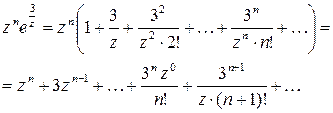
тепер, якщо  , то лишок функції, який за означенням рівний коефіцієнту при
, то лишок функції, який за означенням рівний коефіцієнту при 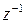 в лорановому розкладі, буде
в лорановому розкладі, буде 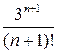 . Якщо ж
. Якщо ж 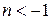 , то в наведеному розкладі в ряд Лорана не буде члена з
, то в наведеному розкладі в ряд Лорана не буде члена з 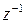 (наприклад, при n =—2 розклад матиме вигляд
(наприклад, при n =—2 розклад матиме вигляд  .). Отже,
.). Отже, 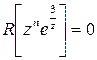 в цьому випадку.
в цьому випадку.
А тому тоді  .
.
Остаточно маємо:

(Нагадуємо, що 0! за означенням рівний 1).
Задача № 11. Довести, що функція  відображає конформно верхній півкруг
відображає конформно верхній півкруг 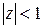 на перший квадрант.
на перший квадрант.
Розв'язання. Функція  є дробово-лінійна, отже, вона перетворює коло
є дробово-лінійна, отже, вона перетворює коло 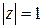 на коло або на пряму в силу кругової властивості дробово-лінійних перетворень. Оскільки точка z=1, яка лежить на колі
на коло або на пряму в силу кругової властивості дробово-лінійних перетворень. Оскільки точка z=1, яка лежить на колі 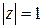 , перетворюється на площині
, перетворюється на площині  в нескінченно віддалену точку, образом кола
в нескінченно віддалену точку, образом кола 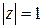 буде пряма (коло нескінченно великого радіуса). Аналогічно і образом дійсної осі у=0 теж буде пряма.
буде пряма (коло нескінченно великого радіуса). Аналогічно і образом дійсної осі у=0 теж буде пряма.
Точки кола відповідно перетворяться в точки 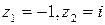 відповідно перетворюється в точки
відповідно перетворюється в точки 
Отже, образом кола 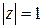 на площині
на площині  буде уявна вісь.
буде уявна вісь.
Аналогічно точки 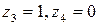 дійсної осі площини відобразяться відповідно у точки
дійсної осі площини відобразяться відповідно у точки 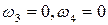 , і образ дійсної осі площини г являтиме дійсну вісь площини
, і образ дійсної осі площини г являтиме дійсну вісь площини  .Позначивши
.Позначивши 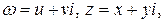 , одержимо:
, одержимо:
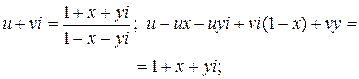
прирівнюючи дійсні і уявні частини в обох частинах рівності, одержимо:
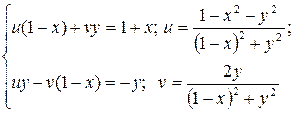
Оскільки для всіх точок всередині круга  , то и>0, до того на верхньому півкрузі у>0, тому
, то и>0, до того на верхньому півкрузі у>0, тому 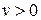 .
.
Таким чином, верхній півкруг площини  відображається на перший квадрант площини
відображається на перший квадрант площини  .
.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 10093; Нарушение авторских прав?; Мы поможем в написании вашей работы!