
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоретичні відомості. Контрольні запитання
|
|
|
|
ДОСЛІДЖЕННЯ СТАТИСТИЧНОЇ ЗНАЧУЩОСТІ РОЗХОДЖЕНЬ У ГРУПАХ
Лабораторна робота № 2
Контрольні запитання
1. Як називають стовпці таблиці вихідних даних?
2. Як називають рядки таблиці вихідних даних?
3. Яка ширина стовпця в електронній таблиці за замовчуванням?
4. Як задати кількість десяткових розрядів числа?
5. У якому вигляді задають змінну у формулах?
6. Яких значень можуть набувати ранги?
7. Коли задають змінні для аналізу?
8. Який розмір має нова (порожня) таблиця вихідних даних?
9. Що можна визначити у вікні «Специфікація змінних»?
10. Що міститься в додатковій інформації електронної таблиці?
11. У якому форматі розташовано «внутрішнє» подання дат в пакеті STATISTICA?
12. Який модуль використовують у цій лабораторній роботі?
13. Який метод вибирають зі стартового вікна у цій роботі?
14. Звідки використано вихідні дані для даної лабораторної роботи?
15. Які функції можна здійснити методом «Описові статистики»?
16. Які показники можна одержати в меню «Додаткові статистики»?
17. Яке значення має рівень значущості за замовчуванням?
18. На які інтервали розбивають сукупність?
19. Для якого показника будують довірчі інтервали?
20. Який параметр набуває значення 0.95 для довірчого інтервалу?
21. Який вигляд має формула дисперсії?
22. Що таке медіана?
23. Що таке квартильний розмах?
24. Яких значень може набувати коефіцієнт асиметрії?
25. Що характеризує коефіцієнт ексцесу?
26. Чому дорівнює коефіцієнт ексцесу нормального розподілу?
27. Які значення задають на осі абсцис гістограми?
28. Які значення задають на осі ординат гістограми?
29. Як обчислюють медіану в інтервальному ряді?
30. Про що свідчить мультимодальність?
31. Яким є нормальний розподіл (симетричним або мультимодальним)?
32. Яку кількість параметрів має нормальний розподіл?
33. Відповідність якому розподілу перевіряють за гістограмою?
34. За яким критерієм перевіряють відповідність заданому розподілу?
35. Які квартилі обчислюють для рядів розподілу?
36. Яку формулу має коефіцієнт асиметрії?
Мета роботи: одержати навички аналізу статистичних залежностей у вихідних даних.
Завдання:
1. У модулі «Основні статистики й таблиці» відкрити вихідний файл даних.
2. Виконати статистичний аналіз залежності даних, використавши один з таких методів:
– дисперсійного аналізу;
– аналізу за t-критерієм (незалежні вибірки);
– аналізу за t-критерієм (залежні вибірки).
3. Оформити звіт про виконання роботи, який містить:
– таблиці числових результатів;
– графічні ілюстрації;
– висновки за результатами виконаного статистичного аналізу (характеристику всіх отриманих результатів).
Використання t-критерію дозволяє порівнювати середні значення у двох групах. Його можна застосовувати навіть у таких випадках, якщо розміри вибірок невеликі (десять одиниць і менше) і якщо змінні нормально розподілені в середині груп, а дисперсії спостережень у групах не є занадто різними.
Критерій застосовують для залежних і незалежних вибірок. При цьому вибирають залежну змінну (їх може бути декілька) і одну групувальну змінну. Основною характеристикою є рівень значущості t-критерію, він має бути менше 0.05 (іноді допускається рівень 0.1). Його значення свідчить про ймовірність помилки гіпотези, що розходження між групами (їх середніми) існують.
Застосування t-критерію для незалежних вибірок. При використанні t- критерію для незалежних вибірок необхідно, щоб вихідні дані мали хоча б одну незалежну змінну (наприклад, стать: чоловік/жінка) і одну залежну змінну (наприклад, тестове значення деякого показника: кров'яний тиск, число лейкоцитів та ін.). За допомогою спеціальних значень незалежної змінної, які називають кодами, дані поділяють на дві групи. Наприклад, можна проаналізувати дані за допомогою t- критерію, який дозволяє порівнювати середнє число лейкоцитів 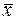 у чоловіків (М) і жінок (W)(табл. 2.1).
у чоловіків (М) і жінок (W)(табл. 2.1).
Для незалежних вибірок результатом тестування за критерієм є таблиця, де для кожної залежної змінної виводять рядок значень: середні значення в першій і другій групах; значення t- критерію; кількість степенів вільності (n – 2); рівень значущості; кількість одиниць у кожній групі; середні квадратичні відхилення в групах; значення функції розподілу Стьюдента.
Аналіз даних за допомогою t- критерію, порівняння середніх значень і відхилення від середніх величин у групах можна виконувати за допомогою діаграм розмаху (рис. 2.1), які дозволяють візуально оцінити ступінь залежності між групувальною змінною й залежними змінними.
Таблиця 2.1
Приклад вихідних даних незалежних вибірок
| № п.п | Стать | x |
| M | ||
| M | ||
| M | ||
| W | ||
| W | ||
Середнє для M  = 110 Середнє для W = 110 Середнє для W 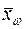 = 103 = 103
|

Рис. 2.1. Діаграма розмаху
Застосування t-критерію для залежних вибірок. Ступінь розходження між середніми величинами у двох групах залежить від значень внутрішньогрупової дисперсії змінних. Залежно від розходжень внутрішньогрупових дисперсій для кожної групи «різниця» між груповими середніми свідчить про більш сильний або більш слабкий степінь залежності між групувальною змінною й залежними змінними. Наприклад, якщо середнє число лейкоцитів  = 102 для чоловіків і
= 102 для чоловіків і 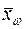 = 104 для жінок, то різницю внутрішньогрупових середніх, що дорівнює двум, можна вважати значною, коли всі значення x для чоловіків містяться в інтервалі 101…103, а всі значення x для жінок – в інтервалі 103…105. Однак, якщо ця різниця отримана з широкого діапазону розкиду даних (наприклад, що змінюються в межах від 0 до 200), то цією різницею можна знехтувати.
= 104 для жінок, то різницю внутрішньогрупових середніх, що дорівнює двум, можна вважати значною, коли всі значення x для чоловіків містяться в інтервалі 101…103, а всі значення x для жінок – в інтервалі 103…105. Однак, якщо ця різниця отримана з широкого діапазону розкиду даних (наприклад, що змінюються в межах від 0 до 200), то цією різницею можна знехтувати.
Таким чином, зменшення внутрішньогрупової варіації (дисперсії)приводить дозбільшення чутливості критерію.
Застосування t- критерію для залежних вибірок доцільно тоді, коли джерело внутрішньогрупової варіації може бути визначено й виключено з аналізу. Це відноситься до двох груп експериментів з однією сукупністю суб'єктів, які підлягали тестуванню двічі. Набір даних, наведених у табл. 2.2, може бути проаналізовано за допомогою t- критерію для залежних вибірок.
Таблиця 2.2
Приклад вихідних даних залежних вибірок
| № п.п | x “до” | x “після” |
| 111.9 | ||
| 80.9 | ||
Середня різниця "до" і "після"  = 1 = 1
|
Дисперсійний аналіз є одним з методів статистичного вивчення залежності результуючої ознаки від ознаки, за якою сукупність розбивається на групи. Цю задачу розв’язують, порівнюючи міжгрупову й внутрішньогрупову дисперсії, розраховані на один степінь вільності. Такі дисперсії називають оцінними. Якщо відношення оцінних дисперсій знаходяться вище теоретичної межі, то можна вважати, що розходження середніх величин за групами значні й існує зв'язок між групувальною і результуючою ознаками.
Розглянемо групування статистичних даних за однією ознакою. При виконанні дисперсійного аналізу як міру варіації ознаки використовують суму квадратів відхилень ознаки від середньої арифметичної, яку називають девіацією.
Припустимо, що існує статистична сукупність, яка складається з k груп, а чисельність i- ї групи дорівнює ni . Тоді статистичні дані можна впорядкувати таким чином:
перша група:  ;
;
друга група: 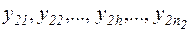 ;
;
…
i- та група: 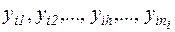 ;
;
…
k- та група: 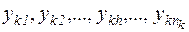 .,
.,
де  ,
, 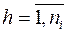 .
.
Загальну середню позначимо  , а середню за групами –
, а середню за групами – 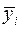 . У формулі
. У формулі  помножимо обидві частини на n, одержимо розклад девіації у вигляді
помножимо обидві частини на n, одержимо розклад девіації у вигляді
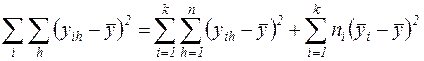 .
.
Загальна девіація ознаки є сумою внутрішньогрупової й міжгрупової девіацій. Для одержання оцінних дисперсій необхідно поділити девіації на відповідні їм числа степенів вільності (табл. 2.3).
Таблиця 2.3
Формули для розрахунку оцінних дисперсій
| Девіація | Степінь вільності | Оцінна дисперсія |
Загальна

| n – 1 | 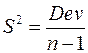
|
Внутрішньогрупова

| n - k | 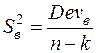
|
Міжгрупова
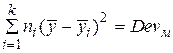
| k – 1 | 
|
Критерієм значущості зв'язку між ознакою, покладеною в основу групування, й результуючою ознакою є критерій Фішера, який розраховують за формулою
 .
.
Для нормально розподіленої ознаки визначено теоретичний роз-поділ відношень цих дисперсій. На основі цього розподілу складено таблиці, що дозволяють зробити висновок про гранично високу величину Fтабл критерію F при відповідних рівнях значущості  . Якщо F > Fтабл, можна стверджувати, що між групувальною і результуючою ознаками існує взаємозв'язок.
. Якщо F > Fтабл, можна стверджувати, що між групувальною і результуючою ознаками існує взаємозв'язок.
При виконанні лабораторної роботи в модулі «Класифікація і однофакторний дисперсійний аналіз (ANOVA)» вибирають залежні й групувальну змінні. Далі вихідні дані розбивають на дві групи. У результаті дисперсійного аналізу одержують таблицю при заданому рівні значущості, у якій кожній залежній змінній відводиться один рядок. Як приклад такий рядок наведено у табл. 2.4.
Таблиця 2.4
Результат дисперсійного аналізу
| Змінна | SS | Ст. в. | MS | F | SSerror | pf | MSerror | p |
| Var1 | 24.0 | 1.0 | 24.0 | 24.0 | 4.0 | 4.0 | 1.0 | 0. 008 |
Як видно, загальну суму квадратів  = 28 (див. табл. 2.4) поділено на компоненти (девіації): суму квадратів SSerror = 4, обумовлену внутрішньогруповою девіацією (
= 28 (див. табл. 2.4) поділено на компоненти (девіації): суму квадратів SSerror = 4, обумовлену внутрішньогруповою девіацією (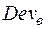 ), і суму квадратів SS =
), і суму квадратів SS =
= 24, обумовлену розходженням середніх значень між групами (міжгруповою девіацією ( )). Міжгрупова оцінна дисперсія MS (
)). Міжгрупова оцінна дисперсія MS (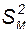 )
)
у табл. 2.4 – це сума квадратів відхилень SS (  ), поділена на число степенів вільності (k – 1 ):
), поділена на число степенів вільності (k – 1 ):
 ,
,
внутрішньогрупова оцінна дисперсія ( )
)

Внутрішньогрупову мінливість SSerror (девіацію 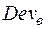 ) називають залишковим компонентом, або дисперсією помилки.
) називають залишковим компонентом, або дисперсією помилки.
Перевірка значущості в дисперсійному аналізі полягає у порівнянні дисперсій за допомогою F- критерію, що дозволяє визначити, чи дійсно відношення дисперсій значно більше одиниці:
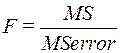 .
.
У розглянутому прикладі F- критерій свідчить про те, що розходження між середніми величинами є значущим (на рівні p = 0.008).
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 435; Нарушение авторских прав?; Мы поможем в написании вашей работы!