Теоретические основы. Удобным объектом для изучения особенностей кинетики химических превращений является реактор смешения пе­риодического действия

Удобным объектом для изучения особенностей кинетики химических превращений является реактор смешения пе­риодического действия.

Режим идеального смешения характеризуется следую­щими допущениями:

- мгновенное изменение и выравнивание технологических параметров по объему реактора;

- равенство значений технологических параметров на выхо­де и в объеме реактора.

На основании сформулированных допущений можно за­писать определение модели идеального смешения для ис­ходного компонента А:

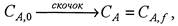
где C _{A, 0}; C _A и С _A,f - концентрация вещества А начальная, текущая и конечная соответственно.

В периодическом реакторе идеального смешения в соот­ветствии с допущениями идеальности значения концентра­ции реагентов, степени превращения, температуры, скоро­сти реакции и других параметров в любой момент времени будут одинаковы во всех точках реактора, однако значения тех же параметров для одной и той же точки в разные мо­менты времени будут отличаться (рис. 5.1). Таким образом, процесс, протекающий в периодическом реакторе, является нестационарным.

Для определения кинетических параметров химической реакции может быть использовано уравнение материально­го баланса реактора идеального смешения периодического действия

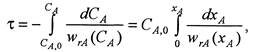
(5.1)

где τ - время пребывания реакционной смеси в реакторе, необходимое для достижения степени превращения реаген­та x _A ; w _rА(С _A) или w _rA(x _A) - кинетическое уравнение реак­ции.

В данной работе изучают кинетику реакции второго по­рядка - омыления щелочью этилового эфира уксусной ки­слоты (этилацетата - ЭТА):

СН₃СООС₂Н₅ + NaOH → CH₃COONa + C₂H₅OH

(A + B → R + S) (5.2)

Кинетическое уравнение такой реакции имеет вид

w _rA = kC_AC_B = kС _A(C _B,0 – С _A,0 + С _A) (5.3)

где k - константа скорости химической реакции.

Представим уравнение (5.3) в виде

w _rA = kf (C _A)

Тогда уравнение (5.1) можно записать как

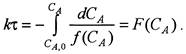
(5.4)

В соответствии с уравнением (5.4) зависимость между F (C _A) и τ является линейной; по величине тангенса угла наклона прямой линии можно определить константу скоро­сти реакции.

Для этого по полученным в эксперименте значениям концентраций реагентов в разные моменты времени строят зависимость

F (C) = φ(τ).

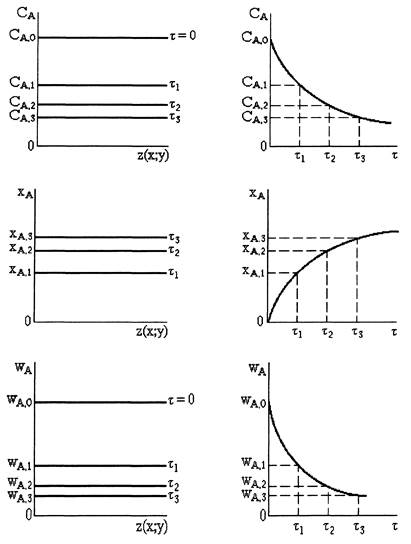
Рис. 5.1. Характеристики периодического реактора идеального смешения

Так как экспериментальные точки обычно характеризу­ются некоторым разбросом, то при построении линейной зависимости целесообразно использовать метод наименьших квадратов (МНК). Конкретный вид функции для необ­ратимой химической реакции второго порядка зависит от того, взяты ли реагенты в стехиометрическом соотношении или нет.

Если щелочь взята в избытке по отношению к этилацетату в Μ раз, т.е. С _B,0 /С _A,0 = М, то с учетом стехиометрических соотношений можно записать

С _B = С _B,0 – С _A,0 + С _A = С _A,0 (М - х_A) (5.5)

Тогда

w _rA = kC ²_A,0(1 - x _A)(M - x _A) (5.6)

Уравнение материального баланса (5.1) после соответст­вующей подстановки примет вид

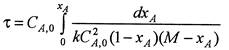
(5.7)

После интегрирования уравнения (5.7) получим

k τ = F ₁(С _B), (5.8)

где

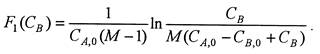
В координатах F ₁(С _B) - τ для реакции второго порядка (в случае M ≠ 1) экспериментальные точки должны находить­ся на прямой линии, тангенс угла наклона которой равен k (рис. 5.2).

Для случая C _A,0 = С _B,0 кинетическое уравнение реакции можно записать в виде

w _rА= kC _А² (5.9)

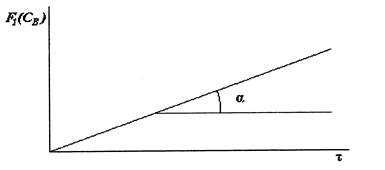
Рис. 5.2. Зависимость F ₁(С _B) от времени пребывания реагентов в периодическом реакторе

После подстановки уравнения (5.9) в уравнение матери­ального баланса (5.1) получаем

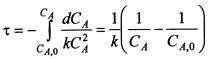
(5.10)

или

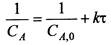
(5.11)

Уравнение (5.11) представляет собой прямую линию в координатах 1 /С _A- τ, отсекающую на оси ординат отрезок 1 /С _A,0 (рис. 5.3).

Построив по экспериментальным точкам в этих коорди­натах прямую линию, по тангенсу угла наклона находим значение константы скорости k.

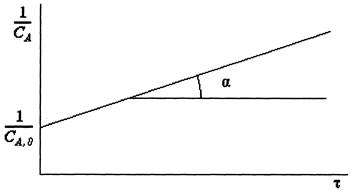
Рис. 5.3. К определению константы скорости реакции для опытов со стехиометрической смесью реагентов

Для определения энергии активации Ε используем урав­нение Аррениуса

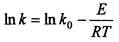
(5.12)

Построив линейную зависимость In k = f (1/ T), можно рассчитать энергию активации по величине тангенса угла наклона этой прямой

tgα = - E/R,

где R = 8,314 Дж-моль^-1К^-1.

Дата добавления: 2015-06-04