Вынужденные колебания под действием синусоидальной силы

Кибернетика второго порядка как парадокс

Образование схем

Здесь Луман возвращается к вопросу о том, как категоризируются объекты внимания массмедиа.

Наблюдение предполагает наблюдателя. Наблюдатель второго порядка видит наблюдателя первого порядка. Но он не видит себя. Система массмедиа сообщает о фактах и мнениях, т. е. о чужих наблюдениях. Она оперирует на уровне наблюдения второго порядка. Но какой наблюдатель наблюдает ее операции? Конечно, она сама может сделать их объектами наблюдения. Но она не задается вопросом: как я наблюдаю, какие провожу различения? Она невидима для себя как наблюдатель и не может не оставаться невидимой в указанном смысле. Таким образом, здесь возникает парадокс наблюдателя, который может преодолеть другой наблюдатель. Таким наблюдателем может быть, например, социолог. Именно как социолог Луман завершает свою книгу вопросом, поставленным в самом начале. Вопрос состоит не в том, говорит он, вспоминая известную формулу Витгенштейна, что происходит, что окружает нас как мир и общество. «Напротив, вопрос в том, как можно принимать информацию о мире и обществе в качестве информации о реальности, если мы знаем, как эта информация производится» (с. 215).

Александр Филиппов

[*] Niklas Luhmann. DIE REALITAT DER MASSENMEDIEN. 2., erweiterte Auflage. Opladen: Westdeutscher Verlag, 1996. 219 S.

[1] В данном случае термин Ausdifferenzierung, употребляемый Луманом, означает процесс функциональной дифференциации системы современного общества, приводящий к выделению и обособлению новой системы (с. 10).

[2] Конечно, исключения возможны, добавляет Луман. Но в этом случае речь идет о коммуникациях в условиях студии, которые воспринимаются как инсценировки.

[3] См. подробное изложение недавно изданного лекционного курса Лумана 1991/1992 годов в нашем обзоре «Теория систем: аутопойесис продолжается» на сайте журнала «Социологическое обозрение» [http://www.sociologica.ru/ или http://www.sociologica.net/].

[4] Следует иметь в виду равносильный перевод «общественность» — в частности потому, что Луман различает «общественность» (Offentlichkeit) и «общественное мнение» (offentliche Meinung).

Колебания, которые совершаются под действием только внутренних сил колебательной системы, называются собственными колебаниями. Частота таких колебаний – собственная частота.

Колебания, возникающие под действием внешней периодически изменяющейся силы или э.д.с., называются вынужденными механическими или вынужденными электромагнитными колебаниями.

Дифференциальное уравнение вынужденных колебаний гармонического осциллятора (шарик на пружине) под действием внешней силы F = F₀ sinωt без учета трения имеет вид

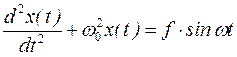(1)

f = F₀/m – приведенная сила

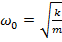– собственная частота

Решение уравнения (1):

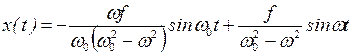(2)

1 слагаемое описывает свободные сопровождающие колебания с частотой ω₀

2 слагаемое описывает вынужденные колебания с частотой ω

Дифференциальное уравнение вынужденных колебаний гармонического осциллятора с учетом трения имеет вид:

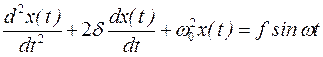(3)

δ – коэффициент затухания

Решение линейного неоднородного дифференциального уравнения вынужденных колебаний (3) равно сумме общего решения однородного уравнения (при равенстве нулю правой части уравнения) и частного решения неоднородного уравнения:

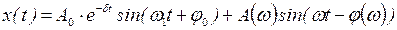(4)

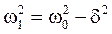
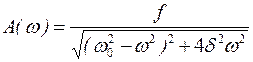(5) – амплитуда вынужденных колебаний

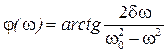(6) – начальная фаза вынужденных колебаний

w – круговая частота вынужденных колебаний.

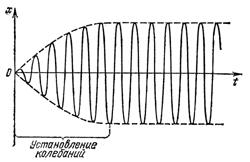Первое слагаемое играет существенную роль только при установлении колебаний до тех пор, пока амплитуда вынужденных колебаний не достигнет значения, определенного уравнением для А (w).

x

В установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими. Амплитуда и фаза вынужденных колебаний также зависят от w.

В установившемся режиме

x(t) = A(w) × cos[wt – j(w)]. (7)

Дата добавления: 2015-06-04