Уравнение бегущей плоской синусоидальной волны

Бегущими волнами называются волны, которые переносят в пространстве энергию.

Уравнением волны называется выражение, которое дает смещение колеблющейся частицы как функцию ее координат и времени.

Рассмотрим плоскую синусоидальную волну (см. рисунок). Волновые поверхности перпендикулярны оси х.

Смещение x будет зависеть только от х и t

x = x (x,t)

Рассмотрим частицу В, находящуюся от источника колебаний О на расстоянии х. Если колебания точек, лежащих в плоскости х =0, описывается функцией

x(O, t) = A × cos w t

то частица В колеблется по тому же закону, но ее колебания отстают на время

,

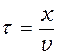где v – скорость распространения волны.

Тогда уравнение бегущей плоской синусоидальной волны запишется так

.

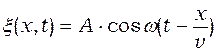Если плоская волна распространяется в противоположном направлении, то

.

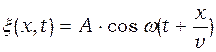В общем случае уравнение бегущей плоской синусоидальной волны для среды, не поглощающей энергию, запишется так:

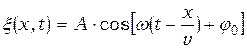
А – амплитуда волны,

w – круговая (циклическая) частота волны;

j₀ – начальная фаза колебаний, определяемая в общем случае выбором начал x и t.

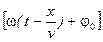– фаза плоской волны.

Для характеристики волн используется волновое число

.

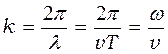Уравнение волны можно записать

x (x,t) = A × cos(w t – kx + j₀)

Пусть при волновом процессе фаза постоянна,т.е.

.

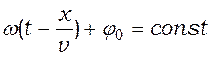Продифференцировав это выражение и сократив на w, получим

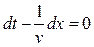
откуда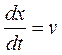

Следовательно, скорость 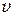распространения волны есть скорость перемещения фазы волны, ее называют фазовой скоростью.

Из выражения для волнового числа вытекает, что фазовая скорость

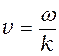
Если фазовая скорость волн в среде зависит от их частоты, то это явление называют дисперсией волн, а среда, в которой наблюдается дисперсия волн, называется диспергирующей средой.

Дата добавления: 2015-06-04