Автоматизированное проектирование плана и продольного профиля. Общий методологический подход

В основе действий проектировщика при проектировании плана и продольного профиля автомобильных дорог всегда лежат определенные способы (принципы). И если способ действия компьютера удается предвидеть достаточно точно, то выбор способа действия человека не является столь же определенным. В настоящее время, когда в проектировании все более активно применяют компьютерные технику и технологий, можно говорить о способах и действиях «человеко-машинных» систем. Вопрос оптимального соотношения составляющих таких систем остается недостаточно изученным.

В свою очередь метод как научная категория лежит в основе осознанного рационального способа действия. Для существования метода необходимы:

правила поведения как описание способа действия;

осознание использования метода как основы действия;

строгое подчинение правилам поведения;

описание ситуаций, в которых данный метод целесообразен.

Анализируя проектную деятельность с позиций частного и общего, можно сказать, что в ее основе лежат, действия, способы (принципы), методы.

В зависимости от средств реализации творческого процесса различают:

эвристические методы;

алгоритмические методы.

В эвристических методах определяющее значение имеют:

ассоциативные способности;

интуитивное мышление;

способы управления мышлением.

Эвристические методы основаны на использовании общих правил и рекомендаций. Они помогают при поиске различных понятий и утверждений, которые позволяют благодаря случайным или логическим ассоциациям открыть или создать абстрактное соотношение, способное дать решение задачи.

Алгоритмические методы основаны на алгоритмах, которые можно определить как последовательность указаний, касающихся процедур (операций), позволяющих решить задачу. Можно выделить:

логические алгоритмы;

математические алгоритмы.

Традиционный принцип трассирования дорог, который принято называть принципом «тангенциального трассирования», до сих пор является доминирующим в практике проектирования в подавляющем большинстве проектных организаций. Методы, которые основаны на этом принципе, относятся к эвристическим. Суть этих методов заключается в том, что назначают тангенциальный ход, в каждый излом которого последовательно вписывают закругления определенных параметров. И если расчет закруглений содержит определенный математический алгоритм, то способ назначения самого тангенциального хода основывается лишь на интуиции и профессиональном опыте инженера-проектировщика.

Трассирование по принципу «гибкой линейки» (см. главу 9) содержит огромный потенциал развития, поскольку при этом осуществляют непосредственную укладку трассы автомобильной дороги, а расчет базиса (тангенциального хода для выноса трассы в натуру) не оказывает влияния на формирование эргономических и эстетических свойств самой трассы. По этой же причине тип закруглений может быть сколь угодно сложным в смысле комбинации геометрических элементов трассирования.

Методы трассирования, содержащие этап графической проработки трассы на картах или топографических планах местности, относятся, безусловно, к эвристическим, поскольку содержат операции интуитивного характера. И в этом смысле ряд методов трассирования по принципу «гибкой линейки» также следует относить к эвристическим. Это и проектирование продольного профиля по методу Союздорпроекта и распространенный метод «опорных элементов» для трассирования автомобильных дорог в плане.

Методы «граничных итераций» Е.Л. Фильштейна и «проекции градиента» В.И. Струченкова для проектирования продольного профиля следует по этой же логике отнести к алгоритмическим. Заметим, что переход к алгоритмическим методам стал возможным лишь благодаря переходу к новой математической (геометрической) сущности трассы. И в том и другом случае в качестве математической модели трассы применяют однородную полилинию, состоящую из отрезков прямых. Очевидно, что полилиния, состоящая из отрезков кривых высокой гладкости склейки, будет еще более приемлемой в качестве модели трассы автомобильной дороги. Но и в том и другом случае речь идет о сплайн-функциях.

Суть алгоритмических методов состоит, как правило, в том, что создается область возможных решений и далее осуществляется процесс поиска наилучшего решения по некоторому критерию оптимизации. Если распространить этот принцип на трассирование автомобильных дорог в плане, то это означает, что проектировщик должен обосновать зону (полосу) варьирования трассы, задать условия (целевую функцию или функционал) оптимизации и применить некоторый математический аппарат оптимизации.

С позиции надежности конечного результата, как показывает практика, выбор трассы посредством назначения зоны варьирования с последующей оптимизацией положения проектируемой трассы является более эффективным, чем назначение одного или нескольких вариантов трассы на основе эвристического подхода.

28.2. Методы «однозначно определенной оси»

Методы «однозначно определенной оси» реализуют, как правило, на основе принципа «тангенциального трассирования». Феномен широкой применимости этого принципа можно объяснить тем, что для проектировщиков этот принцип привычен и потому более понятен, методы на его основе просты в расчетах и обеспечивают предельную экономичность полевого этапа работ.

Рассматривая детально этот принцип трассирования, можно заметить, что при «тангенциальном трассировании» трасса характеризуется ломаной линией, в изломы которой вписаны кривые. Отрезки прямых представляют собой касательные к кривым, поэтому можно говорить о ломаной как о тангенциальном ходе (полигоне). Полевое трассирование состоит, при этом, в последовательном вешении прямых линий тангенциального хода, отыскании и закреплении его вершин, измерениях углов поворота и расчетах пикетажного положения главных точек трассы (НК - начало кривой, КК - конец кривой, СК - середина кривой и т.д.) при заданных значениях радиусов закруглений. Рациональным в таком подходе является то, что ошибки, возможные при вписывании тех или иных кривых, не оказывают влияния на достоверность расчетов последующих кривых.

С принципом «тангенциального трассирования» практически однозначно связано то обязательное условие, что геодезические изыскания выполняют по «пикетному методу». Его суть заключается в следующем: при измерении линий теодолитного хода с помощью мерной ленты на этой линии закрепляют, как правило, пикеты (стометровые отрезки) и характерные точки трассы (водоразделы, лога, пересечения с автомобильными дорогами и инженерными коммуникациями и т.д.) и главные точки трассы. На каждом последующем отрезке ломаной пикетажное положение точек трассы устанавливают с учетом величины домера для каждой вписанной кривой в соответствующий угол поворота трассы. Далее перпендикулярно закрепленным точкам осуществляют съемку поперечных профилей на ширину полосы отвода. Таким образом, тангенциальный ход предопределяет очертания трассы и является основой для всех последующих геодезических работ. Естественно, что изменение или корректировка этой основы на этапе камеральных работ практически невозможна.

Отдельного рассмотрения требует процедура вписывания кривых в изломы тангенциального хода. Случай, когда закругления представляют собой круговые кривые, является простейшим и его применяют для дорог II-V категорий при R > 2000 м и при R > 3000 м - для дорог I-й категории. Для расчета такого закругления при известном угле поворота (q) и радиусе кривой (R) необходимо вычислить значения тангенса (Т), домера (Д), длины кривой (К) и биссектрисы (Б) (см. разд. 8.1). Когда закругления представлены круговыми кривыми с переходными кривыми, расчет не так однозначен, как в первом случае. При равной длине входной и выходной переходной кривой закругление является симметричным и необходимо рассчитывать те же элементы закругления, что и в первом случае. Если длины входной и выходной переходных кривых не равны между собой, то это случай несимметричного закругления. При его расчете уже отсутствует понятие биссектрисы закругления, что усложняет процесс закрепления и последующей разбивки такого закругления (см. разд. 9.2). В частном случае, если отсутствует круговая вставка между переходными кривыми, то такое закругление называют биклотоидой (симметричной или несимметричной, соответственно).

Случаи коробовой клотоиды и комбинированного закругления являются универсальными и служат для подбора любых очертаний закругления (см. главу 9). Расчет таких закруглений представляет собой достаточно сложную аналитическую задачу. Основы решения для составных закруглений известны, однако на практике реализация этих решений является задачей крайне непростой.

Закругления в виде классического сочетания геометрических элементов «клотоида - круговая кривая - клотоида» наиболее распространены в практике дорожного проектирования, но находят применение и другие типы закруглений (геометрических элементов). Например: кадиоиды 1-го и 2-го типов (проф. А.А. Белятынский), гиперболы и поликлотоиды (канд. техн. наук Ю.А. Фортуна), кубические параболы (канд. техн. наук В.А. Федотов), кривые Безье (д-р техн. наук В.Н. Бойков). Применение этих элементов обосновано соответствующими численными и натурными экспериментами и результатами сравнительного анализа.

Наиболее перспективными геометрическими элементами для проектирования закруглений трассы в составе тангенциального хода являются кривые Безье, которые способны принимать формы и свойства всех вышеприведенных элементов. К тому же кривые Безье являются в общем случае пространственными функциями и способны, как будет показано далее, обеспечивать пространственное (трехмерное) трассирование автомобильных дорог в едином классе функций.

В 1970 году П. Безье (французский математик) подобрал составляющие параметрического кубического многочлена таким образом, что их физический смысл стал очень наглядным и весьма подходящим для целей проектирования дорог по принципу «тангенциального трассирования».

Формула Безье для кубического многочлена (n = 3) имеет следующий вид:

Пусть 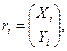i = 0, 1, 2, 3 - тогда для 0 # t # 1

r (t) = r ₀(1 - t)³ + 3 r ₁ t (1 - t)² + 3 r ₂ t ²(1 - t) + r ₃ t ³

или в матричной форме:

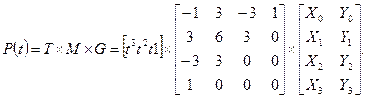
Матрицу М называют базисной матрицей кубической кривой Безье.

Помимо кривой Безье 3-го порядка (кубической) для целей трассирования дорог возможно применение также кривых Безье 2-го, 4-го и 5-го порядков. Соответствующие формулы для вычисления радиусов-векторов (и их производных) для этих кривых приведены ниже.

Кривая Безье 2-го порядка:

r (t) = r ₀(1 - t)² + 2 r ₁ t (1 - t) + r ₂ t ².

Кривая Безье 4-го порядка:

r (t) = r ₀(1 - t)⁴ + 4 r ₁ t (1 - t)³ + 6 r ₂ t ²(1 - t)² + 4 r ₃ t ³(1 - t) + r ₄ t ⁴.

Кривая Безье 5-го порядка:

r (t) = r ₀(1 - t)⁵ + 5 r ₁ t (1 - t)⁴ + 10 r ₂ t ²(1 - t)³ + 10 r ₃ t ³(1 - t)² + 5 r ₄ t ⁴(1 - t) + r ₅ t ⁵.

Кривые Безье, обладающие особыми свойствами, как отмечалось выше, позволяют применять их в качестве универсальных кривых для проектирования закруглений трасс автомобильных дорог. В частности, построение кривой Безье опирается на характеристическую ломаную, которая и предопределяет ее свойства, некоторые их которых приведены ниже:

кривая Безье является гладкой кривой;

касательные в начале и конце кривой совпадают по направлению с первым и последним отрезками ломаной;

кривая Безье лежит в выпуклой оболочке, порожденной массивом точек (опорных вершин) ломаной;

кривая симметрична - сохраняет свою форму при перемене порядка вершин ломаной;

в случае, если вершины ломаной лежат в одной плоскости, то кривая Безье лежит в этой же плоскости;

степень функциональных коэффициентов кривой на единицу меньше количества вершин ломаной;

изменение положения хотя бы одной из вершин ломаной ведет к изменению очертаний кривой Безье.

Поскольку характеристическая ломаная и кривая Безье ассоциативно и функционально находятся в той же взаимозависимости, что и тангенциальный ход с трассой автомобильной дороги, то весьма привлекательно построение кривой Безье интерпретировать в терминах принципа "тангенциального трассирования".

На рис. 28.1,а представлена расчетная схема традиционного закругления «клотоида - круговая кривая - клотоида», вписанного в излом тангенциального хода с вершиной в точке Т и углом поворота q. Расстояние от начала кривой до вершины - тангенс Т ₁. Расстояние от вершины до конца кривой - тангенс Т ₂. Тангенсы Т ₁ и Т ₂ представляют собой касательные в начале и конце составного закругления, пересечение которых в точке Т и порождает характеристическую ломаную ATF. Если провести касательные в узлах стыковки элементов (точки N, М), то получим вспомогательную ломаную ANTMF.

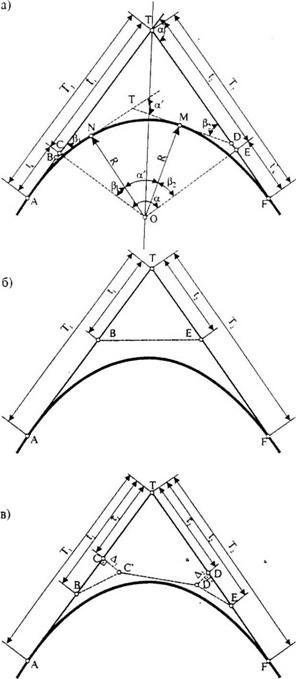
Рис. 28.1. Расчетные схемы закруглений трассы в плане
а - традиционная; б - Безье-3; в - Безье-5

Предположим, что в угол поворота q, образованный сторонами тангенциального хода, требуется вписать закругление трассы посредством кривой Безье 3-й степени (Безье-3). Поставим (см. рис. 28.1, б) начальную А и конечную F точки кривой соответственно на 1-й и 2-й сторонах тангенциального хода. Внутренние точки (В, Е) характеристического многоугольника разместим в вершине утла. Расстояния от заданных точек до вершины будем называть, следуя сложившейся дорожной терминологии, большими тангенсами (Т ₁ и Т ₂). По трем заданным точкам будет построена кубическая кривая Безье со сдвоенной вершиной в точке Т. Если полученные очертания кривой по каким-либо соображениям не устраивают инженера-проектировщика, то варьировать очертаниями кривой можно за счет изменения положения точек В и Е. При этом точки будут перемещаться вдоль соответствующих сторон тангенциального хода. Расстояния от вершины до этих точек условимся называть малыми тангенсами кривой (t ₁, t ₂). Таким образом, варьируя значениями малых и больших тангенсов, можно получать кривые разного очертания и разных дифференциальных свойств. В частности, как будет показано ниже, кривая Безье-3 может с успехом моделировать прямую, дугу окружности, клотоиду и отрезок клотоиды.

Недостатком Безье-3 является то, что при моделировании закругления единой кривой в средней части закругления невозможно добиться участка постоянной кривизны.

Чтобы получить фрагмент дуги окружности в средней части закругления, следует обратиться к кривой Безье 5-й степени (Безье-5), характеристическая ломаная которой состоит из 6-и точек. На рис. 28.1,в эта ломаная образована точками А, В, С, D, Е, F. В терминах тангенциального хода построение Безье-5 выглядит следующим образом. Начальная точка А находится на расстоянии Т ₁ от вершины, точка В - на расстоянии t ₁. Касательная в начале Безье-5 будет совпадать с направлением АВ. Положение третьей точки С условимся отмерять также от вершины Т тангенсом т,, Но если точки А и В могут перемещаться лишь вдоль стороны тангенциального хода, тем самым задавая направление касательной в начале кривой, то точка С может смещаться на Д, влево и вправо от стороны тангенциального хода, формируя разнообразные очертания гладких кривых. Расположение точек D, Е, F на 2-й стороне тангенциального хода сходно расположению точек А, В, С и, поэтому, не требует дополнительных пояснений.

Единой кривой Безье-5 можно также моделировать серпантины 1-го и 2-го рода, левосторонние и правосторонние соединительные рампы на пересечениях в разных уровнях.

28.3. Метод «опорных элементов»

Основные принципы, соблюдаемые при автоматизированном проектировании плана трассы, состоят в следующем: обязательное использование принципов клотоидного трассирования (принцип «гибкой линейки»); детальная, многовариантная проработка трассы с сопоставлением вариантов по основным показателям и выбором наилучшего решения; обеспечение зрительной плавности и ясности трассы и согласование ее с ландшафтом.

При системно автоматизированном проектировании собственно этап трассирования неразрывно связан со всеми последующими этапами проектирования автомобильной дороги и в значительной степени от них зависит. Общая этапная последовательность автоматизированного проектирования плана автомобильных дорог состоит в следующем:

отработка эскизного варианта трассы. С помощью гибкой линейки - сплайна либо от руки сообразно рельефу и ситуации на крупномасштабном плане наносят плавную линию очередного варианта трассы;

автоматизированное проектирование плана трассы. Выполняют компьютерный расчет геометрических элементов плана, координат магистрального хода, координат главных точек (НК, СК, КК и т.д.), пикетов и промежуточных точек и т.д.;

подготовка черного профиля земли по оси дороги. Черный профиль готовят по фиксированному плану варианта трассы с использованием цифровой модели местности ЦММ;

проектирование продольного профиля. Используя профиль земли по оси дороги, а также другие необходимые данные, устанавливают компьютерным расчетом оптимальное (или рациональное) положение проектной линии продольного профиля;

оценка полученного решения по основным показателям. Вариант оценивают по объемам работ, строительной стоимости, транспортно-эксплуатационным расходам, стоимости отвода земель, затратам на борьбу со снегозаносами, уровням удобства и безопасности движения, эстетическим критериям и т.д.;

корректировка плана трассы с последующим повторным проектированием. На основе всесторонней оценки запроектированного варианта трассы, когда проектировщик не удовлетворен теми или иными показателями (большие объемы работ, высокая строительная стоимость, необеспеченная на некоторых участках зрительная плавность и ясность трассы, высокие транспортно-эксплуатационные расходы, необеспеченная видимость, недопустимо высокие значения итоговых коэффициентов аварийности или слишком низкие значения коэффициентов безопасности и т.д.), недостатки проектного решения устраняют путем корректировки плана трассы (в отдельных случаях только продольного профиля) с последующим повторным проектированием варианта дороги.

Задача трансформации эскизной трассы в последовательность сопряженных между собой элементов клотоидной трассы (клотоид, отрезков клотоид, круговых кривых и прямых) решается автоматизированным компьютерным расчетом с использованием аналитических методов, реализованных на базе специального математического аппарата.

Метод «опорных элементов» является одной из разновидностей «методов однозначно определенной оси» впервые разработан в 60-х годах в Германии. В нашей стране метод реализован в виде пакета прикладных программ Союздорпроекта и состоит в том, что с помощью шаблонов круговых кривых и линейки устанавливают положение опорных элементов (прямых и круговых кривых), наилучшим образом аппроксимирующих эскизную трассу автомобильной дороги (рис. 28.2) и в последующей аналитической их увязке.

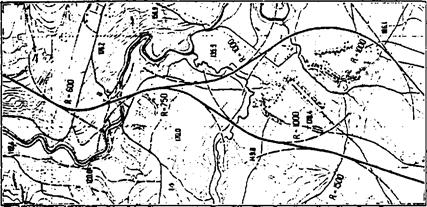
Рис. 28.2. Представление опорных элементов по эскизным вариантам плана трассы

К опорным элементам относят прямые и круговые кривые, которые сопрягаются между собой посредством соединительных элементов - клотоид и отрезков клотоид. Опорные элементы могут быть заданы в общей системе координат фиксированно, полуфиксированно и свободно (рис. 28.3).

Фиксированным считают элемент, для которого определены его тип (прямая, либо круговая кривая), радиус и положение в общей системе координат, не допускающее его перемещения в плане (см. рис. 28.3, а).

Полуфиксированным считают элемент, для которого определены его тип и положение в общей системе координат, допускающее вращение вокруг какой-либо его точки (см. рис. 28.3, б).

Свободным считают элемент, для которого задан его тип, но не определено положение в общей системе координат (см. рис. 28.3, в).

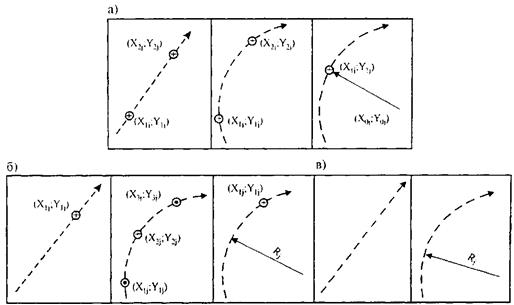
Рис. 28.3. Способы задания опорных элементов:
а - фиксированные; б - полуфиксированные; в - свободные

Предусмотренная возможность задания опорных элементов не только фиксированно, но полуфиксированно и свободно сильно облегчает задачу увязки смежных элементов и позволяет принимать округленные значения параметров или длин соединительных кривых. Возможны 16 различных случаев сопряжения опорных элементов, которые по способу задания элементов разделяют на три группы (рис. 28.4):

I группа (рис. 28.4, а) - оба элемента заданы фиксированно;

II группа (см. рис. 28.4, б) - первый элемент задан фиксированно, второй - полуфиксированно;

III - группа (см. рис 28.4, в) - первый и третий элементы заданы фиксированно, второй - свободно.

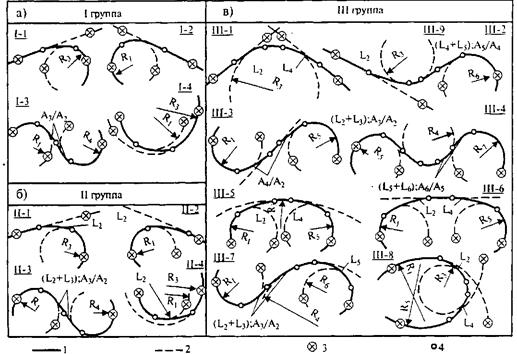
Рис. 28.4. Схемы расчетных случаев:
1 - трасса дороги; 2 - опорный элемент трассы; 3 - фиксированные точки; 4 - главные точки трассы

Для обеспечения автоматизированного анализа при выборе расчетной схемы сопряжения опорные элементы задают с учетом правила знаков (рис. 28.5).

Последовательность проектирования плана по методу «опорных элементов» состоит в следующем:

пользуясь шаблонами круговых кривых и линейкой, по эскизному варианту плана трассы устанавливают положение опорных элементов, радиусы и способы их задания;

с плана снимают исходную информацию, необходимую для автоматической увязки плана трассы на компьютере;

осуществляют автоматический расчет трассы с выдачей необходимой информации.

В результате получают следующие данные, необходимые для дальнейшего проектирования и для выноса трассы в натуру:

параметры геометрических элементов увязанной трассы;

координаты магистрального хода;

координаты главных и промежуточных точек;

таблицы координат для разбивки трассы от магистрального хода по методу прямоугольных координат, методу засечек и по методу полярных координат.

Одно из достоинств метода «опорных элементов» заключается в возможности непосредственного контроля за параметрами и положением всех элементов трассы.

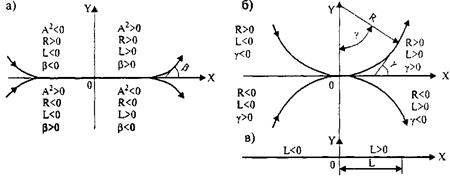
Рис. 28.5. Правило знаков при задании и расчетах элементов трассы
а - клотоид; б - круговых кривых; в - прямых

28.4. Метод «сглаживания эскизной линии трассы»

Метод «сглаживания эскизной линии трассы», разработанный в конце 60-х годов в США и развитый в Германии, заключается в задании координат последовательности точек, снимаемых с эскизного варианта трассы, с последующей аналитической аппроксимацией посредством алгебраических полиномов высоких степеней. В отличие от методов «однозначно определенной оси» в методе «сглаживания эскизной линии трассы» задают избыточное количество точек эскизной линии и в общем случае через все заданные точки не может быть проведена удовлетворительная трасса. Эти точки эскизной линии поэтому рассматривают как «приближенные», вблизи которых должна пройти трасса.

Эскизную трассу заносят в память компьютера координатами последовательности точек с шагом через 10-400 м (в зависимости от извилистости трассы), снимаемых с эскизной линии, нанесенной на крупномасштабный план или аэроснимок от руки, либо с помощью гибкой линейки - сплайна (рис. 28.6, а).

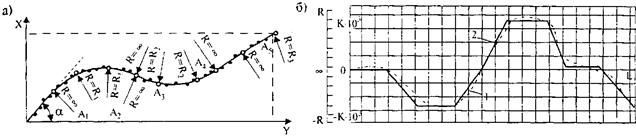
Рис. 28.6. Проектирование плана по методу «сглаживания эскизной линии трассы»:
а - план трассы; б - диаграмма изменения кривизны; J - фактическая кривизна аппроксимирующей функции; 2 - выровненная кривизна

Начальную точку и направление всегда задают фиксированными, поскольку осуществляют отмыкание от ранее запроектированного участка трассы или от существующей автомобильной дороги. Конечную точку трассы можно либо фиксировать, либо задавать свободно. Точкам также придают различные весовые значения, предопределяющие различную степень приближения, либо обязательное прохождение через них аппроксимирующей кривой.

Аналитическую аппроксимацию эскизной трассы, заданной последовательностью точек, осуществляют с использованием алгебраических полиномов высокой степени (обычно 3-й степени), имеющих общую касательную в точках сопряжения.

Y = Ах³ + Вх² + Сх + D, где

А, В, С, D - коэффициенты аппроксимирующих отрезков кривых, определяемых из условия приближения к эскизной линии по методу «наименьших квадратов».

Полученная аналитическая интерпретация эскизной трассы еще не дает возможности контроля за законами изменения кривизны линии, а также за значениями радиусов кривизны в различных ее точках. Чтобы такой контроль мог быть осуществлен, а также с целью представления линии сочетанием обычных элементов клотоидной трассы (прямых, круговых кривых, клотоид и отрезков клотоид) строят диаграмму кривизны (рис. 28.6, б). При этом кривизну проектной линии трассы в любой ее точке определяют:

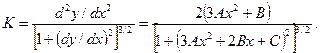
Фактическое очертание диаграммы кривизны заменяют ломаной. Тогда прямые, совпадающие с осью абсцисс, соответствуют прямым участкам трассы, прямые, параллельные оси абсцисс - круговым кривым и наклонные прямые - клотоидам или отрезкам клотоид. Таким образом, в конечном итоге трассу представляют в виде обычных элементов клотоидной трассы.

Одна из разновидностей метода «сглаживания эскизной линии трассы» - метод «аппроксимации последовательности точек» реализован в Союздорпроекте в виде пакета прикладных программ «План». Идея метода «аппроксимации последовательности точек» заключается в компьютерной обработке эскизной линии трассы с целью определения геометрических характеристик и положения элементов клотоидной трассы, отвечающей определенным требованиям, предъявляемых к ней.

Модель эскизной линии трассы в плане представляют упорядоченным множеством точек, определяемым тремя характеристиками: х_i, у_i, р_i, (где х_i и у_i - координаты i -й точки в общей системе координат; р_i - «вес» i -й точки). Задача определения геометрических характеристик элементов трассы и их положения, наилучшим образом приближающихся к заданной эскизной линии, решается с применением методов математического программирования. При этом в качестве целевой функции принято выражение:

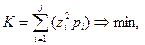где

К - критерий оптимальности;

z_i - расстояние от i -й точки до трассы по нормали.

Обязательными ограничениями являются:

D t _min £ D t £ D t _max;

D R _min £ D R £ D R _max;

D L _min £ D L £ D L _max;

D A _min £ D A £ D A _max; где

D t - изменение центрального утла круговых кривых;

D R - изменение радиуса круговых кривых;

D L - изменение длин прямых;

D A - изменение параметров клотоид;

min, max - индексы, обозначающие нижнюю и верхнюю границы соответствующих переменных.

Пакет прикладных программ «План» Союздорпроекта, кроме того, позволяет рассчитывать координаты главных и промежуточных точек трассы, поперечников трассы, готовить таблицы для разбивки трассы от произвольного магистрального хода по методам: прямоугольных координат, полярных координат и засечек. Пакет прикладных программ «План» обеспечивает получение продольных и поперечных черных профилей земли с использованием ЦММ.

Дата добавления: 2015-06-04