Методы «свободной геометрии». Сплайн-трассирование 2 страница

Задачу проектирования оптимального продольного профиля решают в интерактивном режиме с оценкой промежуточных результатов на экране монитора.

29.3. Метод «граничных итераций»

Метод «граничных итераций» разработан в 1967 году Е.Л. Фильштейном. Метод, реализованный в виде компьютерной программы «Пола», при проектировании оптимальной линии продольного профиля автомобильных дорог позволяет учитывать следующие условия и ограничения:

для каждого элемента продольного профиля уклон проектной линии К_i не должен превышать предельно допустимого значения 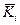. Для обеспечения зрительной плавности и ясности трассы, органического вписывания ее в окружающий ландшафт и достижения в связи с этим высоких уровней удобства и безопасности движения методом предусмотрена возможность дифференцированного задания предельных уклонов 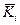на различных участках автомобильной дороги;

в каждой точке проектной линии, представляющей собой плавную кривую переменного радиуса, радиусы кривизны вертикальных выпуклых и вогнутых кривых не должны быть меньше допустимых значени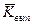й и 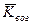. Методом предусмотрена возможность дифференцированного задания допустимых значений радиусов вертикальных кривых на различных участках автомобильной дороги;

высотные отметки проектной линии в специально оговоренных точках, называемых фиксированными, должны быть равными заданным значениям. К этим точкам могут быть отнесены отметки проезжей части мостов и путепроводов, головок рельсов железных дорог и проезжей части автомобильных дорог, пересекаемых в одном уровне, отметки проезда в населенных пунктах и т.д. Фиксированными являются также точки начала и конца проектируемого участка автомобильной дороги;

высотные отметки проектной линии в специально оговоренных точках или зонах, называемых ограничивающими, должны быть не ниже заданных значений. К этим точкам обычно относят отметки пойменных насыпей на подходах к мостам, отметки насыпей на болотах, над трубами, минимальные отметки проезда на мостах и путепроводах, когда их высоты не зафиксированы строго;

отметки точек верха зоны с гидрогеологическими условиями, затрудняющими или делающими нежелательным прохождение проектной линии продольного профиля ниже границы этой зоны. К этим ограничениям, называемым контурными, относят, например, требование проложения проектной линии без выемок, либо с выемками ограниченной глубины. Для этой цели проектировщик задает значение ± h' - расстояние от черной линии, на котором должна находиться параллельная ей ограничивающая линия с указанием начала и конца этой зоны.

При автоматизированном проектировании оптимальной линии продольного профиля должна быть обеспечена минимальная строительная стоимость. Для этой цели задают ориентировочно стоимость 1 м³ грунта насыпи и 1 м³ грунта выемки, которые назначают дифференцированно по участкам проектируемой дороги в зависимости от категории разрабатываемого грунта, способа производства работ, дальности возки и т.д.

Тип поперечного профиля земляного полотна в каждом сечении выбирают в зависимости от рабочей отметки, ее знака и заданных параметров земляного полотна. Метод «граничных итераций» и программа «Пола» предусматривают в процессе проектирования автоматический выбор типа поперечного профиля земляного полотна, задаваемого параметрами основных форм насыпей и выемок (рис. 29.2).

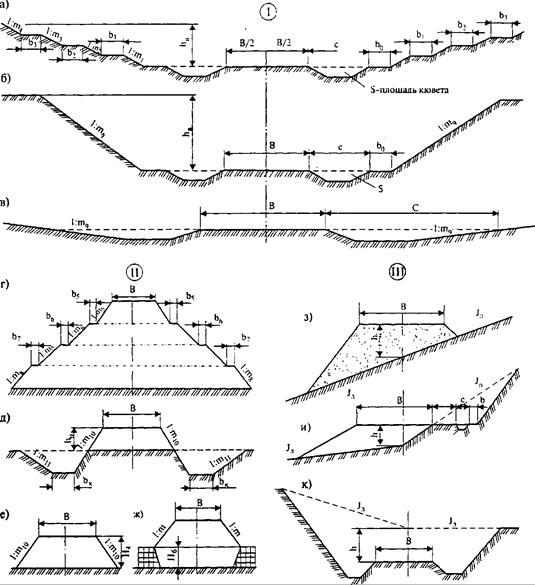
Рис. 29.2. Поперечные профили земляного полотна, используемые при автоматизированном проектировании продольного профиля по программе «Пола-2»

К параметрам земляного полотна относят: его ширину, коэффициенты заложения откосов, ширину берм, размеры кюветов и резервов и т.д. В зависимости от знака и численного значения рабочей отметки при подсчете объемов земляных работ в расчет автоматически вводят соответствующие очертания поперечников земляного полотна.

Стоимость отвода 1 м² земельных угодий, по которым проходит автомобильная дорога, задают с целью учета изменения стоимости строительства, связанного с постоянным отчуждением земель при высотном перемещении проектной линии.

Стоимость искусственных сооружений при автоматизированном проектировании оптимального продольного профиля учитывают заменой участков автомобильных дорог на искусственных сооружениях эквивалентными по стоимости участками земляного полотна.

Автоматизированное определение оптимального положения проектной линии продольного профиля оказывается наиболее эффективным при проектировании автомобильных дорог в пересеченной местности. В этих случаях совершенно необходимым является учет косогорности при подсчетах объемов земляных работ и корректировке проектной линии для отыскания оптимума. Поперечные профили земли, получаемые с использованием цифровых моделей местности (ЦММ) или в результате съемки местности по характерным точкам, преобразуют в двухскатный эквивалентный профиль с точкой перелома, лежащей по оси проектируемой дороги. Для этой цели задают уклоны левой и правой от оси частей поперечника и его пикетажное положение. Очертание косогора в промежуточных сечениях между заданными поперечниками интерполируется автоматически программным путем и учитывается при подсчете объемов земляных работ. Тип поперечного профиля земляного полотна в каждом сечении косогорного участка автоматически выбирается в зависимости от величин рабочих отметок, параметров земляного полотна, положения точек пересечения поверхности косогора с откосами земляного полотна.

Основная идея метода «граничных итераций» состоит в следующем. Для решения поставленной задачи определен класс функций, в котором отыскивается оптимальное решение, - это ломаная линия со строительным шагом, принимаемым обычно равным 20 м. Ломаная с минимально возможным строительным шагом представляет собой дискретный аналог кривой переменного радиуса. Являясь более гибким элементом по сравнению с обычной круговой (или параболической) кривой, она позволяет максимально приближаться к оптимальному решению и обеспечивает большую зрительную плавность и ясность трассы, что для автомобильных дорог (особенно высоких категорий) имеет одно из важнейших значений.

Для получения нулевого (отправного) проектного профиля строят математическую модель профиля земли по оси дороги (черного профиля) в классе ломаных с равным шагом. Как известно, исходный черный профиль всегда представляют в виде ломаной с неравным шагом, уравнение которой имеет вид:

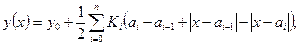где (29.1)

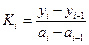- тангенс угла наклона i -го отрезка;

а_i, у_i - соответственно, абсциссы и ординаты ломаной (т.е. черного профиля).

Математическая модель черного профиля в классе ломаной с равным шагом должна наименьшим образом отклоняться от исходного черного профиля, описываемого уравнением (29.1).

Задача оптимизации положения проектной линии продольного профиля сводится к отысканию такого ее положения, при котором достигается:

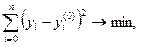(29.2)

при выполнении ограничений:

по уклону

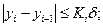при 1< i < п (29.3)

по кривизне

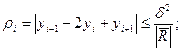(29.4)

по фиксированным точкам

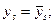(29.5)

по ограничивающим точкам и зонам

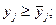где (29.6)

у_i - ординаты проектной линии;

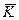- предельно допустимые уклоны;

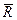- предельные радиусы кривизны для выпуклых и вогнутых вертикальных кривых;

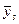- фиксированные точки;

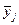- ограничивающие точки и зоны.

Задача отыскания в принятом классе функций такой ломаной, которая удовлетворяла бы заданным ограничениям (29.3-29.6) и в то же время соответствовала минимуму строительной стоимости возведения земляного полотна (29.2), разбивается на два этапа.

На первом этапе отыскивается положение проектной линии продольного профиля, соответствующее минимуму профильных объемов земляных работ при единообразном очертании поперечного профиля земляного полотна.

Нулевым приближением является модель черного профиля земли у ⁽⁰⁾, которое, естественно не может быть окончательным, так как в общем случае для некоторых элементов линии у ⁽⁰⁾ оказываются не выполненными ограничения (29.3-29.6). В связи с этим вначале проектная линия регулируется по величине допустимого уклона. Для этой цели отыскивается какое-либо 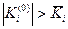, и находят такое решение у ⁽¹⁾, при котором достигается min (у ⁽¹⁾ - у ⁽⁰⁾)² и 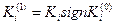. Затем выбирают 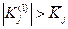и отыскивают такое положение проектной линии у ⁽²⁾, при котором достигается min(у ⁽²⁾ - у ⁽¹⁾)² и 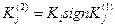и т.д.

Иными словами, на каждом р -м шаге алгоритма накладывается только одно ограничение и ищется минимальное отклонение не от нулевого приближения (у ⁽⁰⁾), а от решения полученного на (р -1)-м шаге алгоритма. В этом заключается основная идея метода «граничных итераций». Возможные расчетные случаи при регулировании продольного уклона представлены в табл. 29.2.

Таблица 29.2.

Расчетные случаи при регулировании продольного уклона

N/n	Схема	Индексы фиксированных ординат	Расчетные формулы
		-
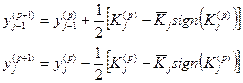
		j - 1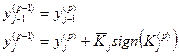
		j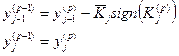
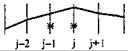
		j - 1; j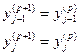
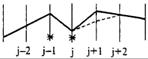
		j - 1; j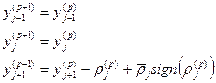
		j, j + 1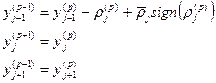
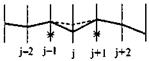
		j - 1, j + 1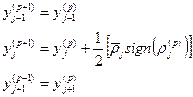
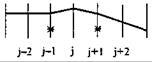
		j - 1; j j + 1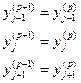

Затем аналогичным образом проектная линия регулируется по кривизне и т.д. Возможные расчетные случаи при регулировании проектной линии по кривизне представлены в табл. 29.3.

Таблица 29.3.

Расчетные случаи при регулировании кривизны

№ п/п	Схема	Индексы фиксированных ординат	Расчетные формулы
		-
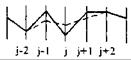
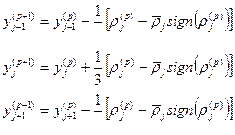
		j - 1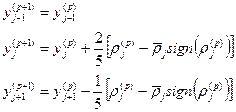
		j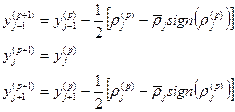
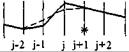
		j + 1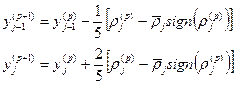

Отличительные особенности метода «граничных итераций» от других методов оптимизации состоят в том, что в процессе поиска допустимого решения не производится прямого вычисления и сравнения функции цели - строительной стоимости. Все промежуточные состояния продольного профиля являются недопустимыми по техническим ограничениям, но каждое последующее состояние имеет невязку в ограничениях меньшую, чем предыдущее состояние. Первое допустимое по техническим ограничениям решение является оптимальным при условии единообразного очертания поперечного профиля и одинаковой стоимости единицы объема земляных работ по всей трассе.

На втором этапе автоматизированного проектирования продольного профиля осуществляется коррекция проектной линии, полученной на первом этапе, е учетом фактического очертания поперечных профилей земляного полотна и с учетом различных стоимостных показателей возведения земляного полотна на различных участках проектируемой автомобильной дороги. Для этого в программе «Пола» использован эффективный эвристический метод коррекции проектной линии продольного профиля.

После определения предварительного положения проектной линии вычисляют рабочие отметки и соответствующие им стоимости каждого условного поперечника на единице длины трассы. Затем в зависимости от численного значения и знака рабочей отметки, параметров истинного поперечного профиля и фактической стоимости 1 м³ грунта вычисляют скорректированную рабочую отметку при условии, что стоимость единицы длины истинного поперечника должна равняться стоимости ранее найденного условного поперечника. Поскольку при этом могут быть нарушены некоторые ограничения, то в результате новой корректировки отыскивают линию, отвечающую условиям (29.3) - (29.6) и минимально отклоняющуюся от скорректированной из условия (29.2).

По полученному профилю производят распределение земляных масс, определяют действительную стоимость разработки грунта на различных участках трассы и получают уточненное положение проектной линии при повторном проектировании по программе «Пола».

29.4. Методы «свободной геометрии»

Действующие нормативные документы допускают, проектирование продольного профиля в классе ломаных линий (см. разд. 29.3). Проектная линия в классе ломаных представляет собой дискретный аналог гибкой кривой переменного радиуса. Ограничения по кривизне в этом случае косвенно обеспечиваются ограничениями на алгебраическую разность уклонов двух смежных отрезков прямых. Необходимость проектирования проектной линии в классе ломаных возникает чаще всего при ремонте и реконструкции автомобильных дорог, когда математическая модель проектной линии в виде последовательности прямых и дуг окружностей (квадратных парабол) оказывается недостаточно гибкой для получения приемлемого проектного решения. Особенно очевидным это становится при проектировании микропрофилирования ремонтируемых покрытий.

При автоматизированном проектировании описание проектной линии в классе ломаных требует определенной математической формализации. Наиболее просто и эффективно эта задача формализуется в терминах и математических построениях сплайн-функций, а ломаная линия собственно и является линейным сплайном или сплайном 1-й степени.

Сплайны 1-й степени (ломаные) достаточно просты для понимания и, в то же время, отражают основные свойства сплайн-функций. С математической точки зрения, сплайн 1-й степени - это кусочно-непрерывная функция, на каждом отрезке описываемая уравнением вида:

у = а_i + b_ix, где (29.7)

i - номер рассматриваемого интервала между узлами интерполяции х_i и x_{i +1}.

Как следует из уравнения (29.7), на элементарном интервале вид уравнения не отличается от общепринятого выражения прямой линии. В целом, уравнение ломаной (сплайна 1-й степени) в матричной форме можно записать как:

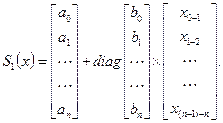(29.8)

Система линейных уравнений (29.8) не требует совместного решения и распадается на решения каждого уравнения в отдельности. Сплайн, решение которого связано с вычислением подсистем небольшой размерности (в данном случае - уравнений первого порядка) является локальным.

Интерполяционный сплайн 1-й степени - это ломаная, проходящая через точки (х_i, у_i). Для совокупности х_i (I = 0, 1,..., п) в интервале [а, b] при этом должно выполняться условие х_i < х_{i +1}. Используя интерполяционный полином Лагранжа можно построить сплайн для интервала i - (i +1):

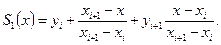
Обозначение S ₁(x) понимается как сплайн-функция 1-й степени. Форму записи этой функции можно преобразовать к виду:

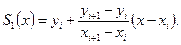
Для построения алгоритма и составления процедуры вычисления линейных сплайн-функций необходимо помнить всего лишь 2 п +2 числа.

На основе интерполяционных сплайнов 1-й степени можно разрабатывать автоматизированные процедуры построения оптимальной проектной линии (см. разд. 26.3) и эвристической проектной линии, получаемой в диалоговом режиме, когда в основе проектного решения лежат интуиция и опыт инженера-проектировщика. Суть проектирования здесь состоит в том, что эскизно намечают ломаную проектную линию и посредством «ручного» перемещения узлов излома этой линии находят приемлемое ее положение с позиции проектировщика.

Другую перспективу открывают сглаживающие линейные сплайны, на основе которых можно строить алгоритмы нахождения оптимального положения ломаной проектной линии.

В случае применения сплайнов 1-й степени функционал цели имеет вид:

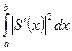
После подстановки первой производной сплайна, совпадающей в данном случае с разделенной разностью, функционал примет вид:

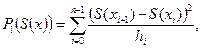где (29.9)

h_i = х_{i +1} - х_i

Продифференцируем выражение (29.9) по переменной S (х_i) и сложим два последовательных слагаемых уравнения, содержащих эту неизвестную:

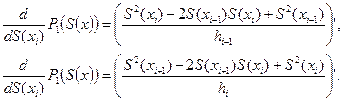
Приравняв полученную сумму нулю и выразив неизвестное S (х_i), получим рекуррентную формулу:

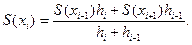
Здесь знак «=» представляет собой оператор присваивания. Если принять шаг интерполяции равномерным, то есть h_i = const, то процесс оптимизации (пошаговых итераций) в графической интерпретации будет вполне понятен (рис. 29.3).

Быстрая сходимость итерационного процесса позволяет рекомендовать этот метод для предварительной выработки проектных решений по проектной линии продольного профиля. В этом случае радиусы кривизны и уклоны проектной линии можно контролировать в системе ограничений посредством построения первых и вторых разделенных разностей.

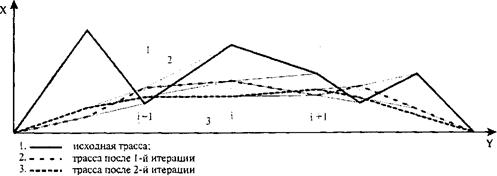
Рис. 29.3. Графическая интерпретация сглаживания линейного сплайна

Следует отметить, что методы «проекции градиента» и «граничных итераций», изложенные в разделах 29.2, 29.3, также реализованы посредством математической модели проектной линии в виде линейных сплайнов.

Более совершенные проектные решения по продольному профилю можно получить, если реализовывать проектную линию в виде функций (сплайнов) более высоких степеней, чем первая. Например, сплайны 3-й степени обладают свойством нелинейного изменения кривизны. Это свойство придает им высокую гибкость изменения формы, что чрезвычайно важно при выработке проектных решений в узкой полосе варьирования (в проектах ремонта и реконструкции автомобильных дорог). К тому же 1-я и 2-я производные этих сплайнов непрерывны, что обеспечивает контроль за величинами радиусов кривизны вертикальных кривых и законами изменения кривизны по длине трассы и в конечном итоге высокую гладкость и плавность проектной линии.

Методы проектирования продольного профиля, основанные на применении сплайнов 3-й степени (кубических), используют для описания проектной линии как интерполяционные, так и сглаживающие сплайны.

Сглаживающие сплайны необходимы для поиска оптимального положения проектной линии в заданной полосе варьирования. А интерполяционные сплайны позволяют обеспечить процесс корректировки проектной линии в интерактивном режиме работы инженера-проектировщика при эвристическом проектировании.

Для описания проектной линии на каждом интервале в виде интерполяционного кубического сплайна применяют или естественный сплайн вида:

Z_s = Z_i + B_i (S - S_i) + C_i (S - S_i)² + D_i (S - S_i)³, S_i £ S £ S_{i +1}.

или рациональный сплайн вила:

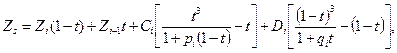где

t = (S - S_i)/ h_i, h_i = S_{i +1} - S_i, p_i, q_i - заданные числа, -1 < p_i, q_i < ¥.

Рациональный сплайн обладает свойствами изменения формы на любом интервале за счет варьирования величинами коэффициентов p_i, q_i, что дает возможность гибкого и точного приближения проектной линии к форме рельефа или существующим очертаниям реконструируемой (ремонтируемой) автомобильной дороги.

Сглаживающие кубические сплайны, применяемые для оптимизации положения проектной линии, как правило, минимизируют функционал вида:

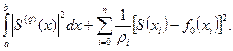
Вычисление сглаживающих сплайнов 3-й степени осуществляют методами «покоординатного спуска» или «штрафных функций».

Современные системы автоматизированного проектирования автомобильных дорог содержат, как правило, алгоритмы построения проектных линий продольного профиля как на основе традиционного математического аппарата (прямые, круговые кривые, квадратные параболы), так и на основе сплайн-функций.

ГЛАВА 30. АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ ОПТИМАЛЬНЫХ НЕЖЕСТКИХ ДОРОЖНЫХ ОДЕЖД

Дата добавления: 2015-06-04