Математическое моделирование стока ливневых вод с малых водосборов

Одна из первых математических моделей стока была разработана еще в 1931г. М. М. Протодьяконовым, однако в связи с многодельностью расчетов и отсутствием в то время компьютерной техники она широкого распространения не получила.

Появление и стремительное совершенствование компьютерной техники предопределило ускоренное развитие методов математического моделирования, в частности, моделирования процесса формирования и стекания стока ливневых вод с водосборов.

Процесс формирования стока на каждом конкретном водосборе - сложнейшее природное явление. На него оказывает влияние большое количество независимых факторов, оценка которых затруднена из-за пространственной и временной их изменчивости.

Одна из первых математических моделей стока, реализующая идею проф. М.М. Протодьяконова, была разработана в 1983 году на кафедре проектирования дорог МАДИ (Федотов Г.А. Автоматизированное проектирование автомобильных дорог. - М.: Транспорт, 1986.- 318 с.). Согласно этой модели бассейн любой сложной формы и любых размеров может быть представлен в виде системы эквивалентных по площади прямоугольников, примыкающих к главному логу (рис. 31.1). Учитывая, что время добегания ливневых вод по водосбору играет весьма существенную роль в формировании максимальных расходов, длины схематизированных прямоугольных водосборов целесообразно принимать равными фактическим длинам боковых логов. Тогда средняя ширина каждого схематизированного водосбора i -го бокового лога:

B_i = F_i/L_i, где

F_i и L_i - фактическая площадь и длина водосбора i -го лога, соответственно км² и км.

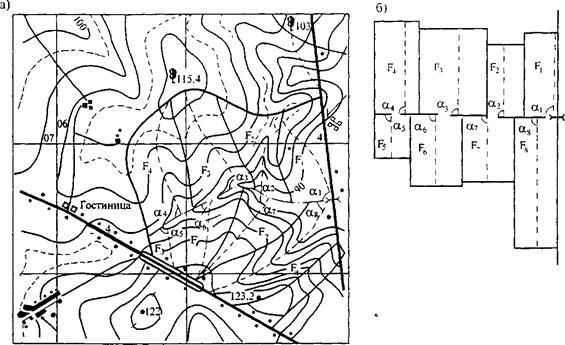
Рис. 31.1. Схематизация водосбора:
а - представление водосборов в плане; б - схематизация в виде эквивалентных по площади прямоугольников

Угол примыкания каждого бокового лога к главному принимают равным углу между направлением тальвега бокового лога и направлением потока в главном логу (см. рис. 31.1).

Полученный на каждый j -й момент времени паводка сосредоточенный расход в устье каждого i -го бокового лога Q_ij представляют в виде равномерно распределенных погонных расходов на фактической ширине каждого бокового лога в устьевой его части:

q_ij = Q_ij / В_yi, где

В_yi - фактическая ширина i -го лога в устьевой его части.

Таким образом, при описании неустановившегося течения ливневых вод по главному логу боковая приточность в каждый j -й момент времени может быть представлена в виде кусочно-постоянной функции (рис. 31.2).

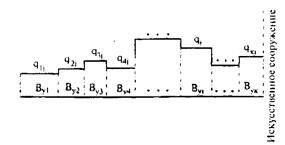
Рис. 31.2. Представление боковой приточности по главному логу в виде кусочно-постоянной функции

Изменение хода дождя и потерь схематизируют исходя из следующего:

в начальный период дождь идет с меньшей интенсивностью, затем усиливается и в конце снова уменьшается;

попадая в почву, осадки впитываются, при этом, если интенсивность впитывания меньше скорости выпадения осадков, то формируется избыточный слой;

часть избыточного слоя в ходе протекания вниз по склонам задерживается растительностью, а часть заполняет различные углубления микрорельефа местности. Эти виды потерь целесообразно учитывать при обработке кривых впитывания;

ход дождя и потерь стока имеют разные интенсивности, вследствие чего избыточный слой формируется только в случае, когда интенсивность выпадения осадков больше интенсивности потерь стока (рис. 31.3).

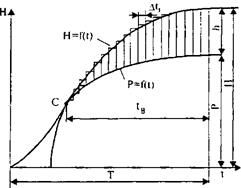
Рис. 31.3. Замена графика хода дождя и впитывания ступенчатым очертанием с шагом D t

Таким образом, можно построить типовые графики хода дождя и потерь (см. рис. 31.3) для каждого ливневого района и решить, какой ход дождя будет наиболее характерным, т.е. предложенная схема определения слоя стока может дополняться сообразно с местными условиями и возможностями.

Для использования этих данных в качестве исходной информации в математической модели формирования ливневого стока кривые хода дождя Н = f (t) и впитывания Р = f (t) заменяют ступенчатым очертанием с шагом по времени D t (см. рис. 31.3).

Для расчета склонового стока на малых водосборах применяют уравнение кинематической волны (схема склонового стока «сплошным слоем»):

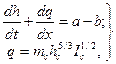где (31.1)

h_c - глубина склонового потока, м;

t - время, сек;

q - погонный расход, м³/с;

х - текущая координата, направленная от водораздела вниз по склону, м;

а - интенсивность ливня, м/с;

b - интенсивность впитывания, м/с;

т_с - показатель ровности склонов (табл. 31.1);

I_с - уклон склона, ‰.

Таблица 31.1.

Показатели ровности поверхности т_с

Морфологические признаки поверхности	Показатель ровности m
Бетонные плиты
Мощение
Засев травой
Незаросшие ровные земляные поверхности; неукрепленные канавы
Русла земляные ровные; русла полугорных рек; незаросшие поймы
Русла земляные извилистые; галечно-валунные; суходолы ровные; поймы, заросшие на 10 %
Русла земляные очень извилистые; суходолы извилистые; поймы, заросшие на 20 %
Суходолы, засоренные камнем и заросшие; поймы, заросшие на 50 %
Поймы, заросшие на 70 %
Поймы, заросшие на 100 %

Систему уравнений (31.1) проще всего решать в конечных разностях по схеме с вперед направленными разностями:

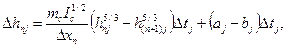где (31.2)

D h_nj - приращение глубины на п -м участке склона за j -й интервал времени D t_j, м;

х_п - расчетный интервал длины, м;

a_j, b_j - интенсивности ливня и впитывания в j -й момент времени, м/с.

Уравнение (31.2) решают последовательно для каждой пары створов сверху вниз по склону, начиная с водораздела для каждого интервала времени (рис. 31.4). При этом в створе на водоразделе (i = 0) принимают глубину h_oj = 0.

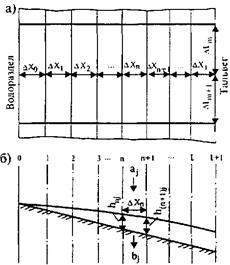
Рис. 31.4. Схема к расчету склонового стока:
а - план; б - продольный разрез

Шероховатости и уклоны склонов могут быть назначены дифференцированно для каждого участка.

Форму живого сечения тальвегов боковых логов и главного лога аппроксимируют многоточечным профилем (рис. 31.5). Такая аппроксимация позволяет с достаточной точностью представлять живые сечения разнообразного очертания, в частности, треугольного, прямоугольного, трапецеидального и т.д.

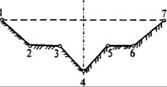
Рис. 31.5. Аппроксимация живого сечения лога семиточечным профилем

Движение ливневых вод по тальвегу главного и боковых логов описывают системой уравнений неустановившегося течения жидкости переменной массы (с боковой приточностью):

динамического

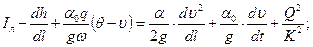(31.3)

неразрывности

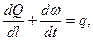где

I_л - уклон дна лога, ‰;

h - глубина потока, м;

l - длина по логу, м;

a₀» 1,03 - коэффициент Буссинеска (корректив количества движения);

q - боковая приточность в единицу времени на единицу длины лога, м³/(с.м);

g - ускорение силы тяжести, м/с²;

w - площадь живого сечения, м²;

q - проекция скорости присоединенных частиц жидкости на направление скорости потока в логу, м/с;

u - скорость потока, м/с;

a» 1,1 - коэффициент Кориолиса (корректив кинетической энергии);

t - время;

Q и К - расход и расходная характеристика, соответственно, м³/с.

Систему уравнений (31.3) решают в конечных разностях:

динамическое уравнение

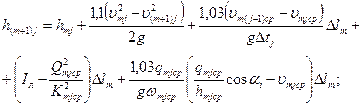(31.4)

уравнение неразрывности

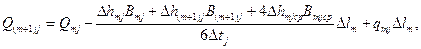где (31.5)

h_mj, h_(m+1)j - глубины потока в m -м и (т +1)-м створах в j -й момент времени, м;

u_mj, u_(m+1)j - соответственно скорости течения в m -м и (т +1)-м створах в j -й момент времени, м/с;

u_{m(j - 1) cp}, u_mjcp - соответственно средние скорости течения в m -м расчетном участке лога в (j -l)-й и j -й моменты времени, м/с;

D l_m - длина т -го участка русла, м;

I_л - уклон лога, ‰;

Q_mjcp, K_mjcp - соответственно расход и расходная характеристика сечения, средние на m -м участке лога в j -м интервале времени, м³/с;

q_mj - боковая приточность на m -м участке лога в j -й момент времени, м³/(с.м);

w_mjcp - средняя на m -м участке лога площадь живого сечения в j -й момент времени, м²;

q_mjcp, h_mjcp - средние на m -м участке лога боковая приточность и глубина в j -й момент времени;

a _i - угол подхода i -го тальвега бокового лога к главному логу;

Q_mj, Q_(m+1)j - соответственно расходы в m -м и (т +1)-м створах в j -й момент времени, м³/с;

D h_mj, D h_(m+1)j - приращения глубины воды в соответствующих створах за время D t_j, м;

B_mj, B_(m+1)j - ширины потока в соответствующих створах, м.

Шероховатости и уклоны тальвегов боковых логов назначают дифференцированно. Шероховатости и уклоны главного лога также можно задавать дифференцированно по его длине.

Последовательность детального расчета ливневого стока с малых водосборов, реализация которого возможна лишь при использовании компьютерной техники, следующая:

расчетный водосбор представляют в виде схематизированных прямоугольных водосборов и определяют исходные параметры (площади, ширины, длины, уклоны, шероховатости и характеристики поперечных сечений тальвегов);

заменяют кривые хода дождя Н = f (t) и впитывания Р = f (t) ступенчатым очертанием с шагом D t_j (см. рис. 31.3);

делят каждый i -й боковой лог по тальвегу, начиная от водораздела до его устья, на необходимое количество расчетных интервалов длины D l_mi;

главный лог по тальвегу также делят на значительное число участков D l_m, начиная от водораздела до замыкающего створа (рис. 31.6);

на первой ступеньке, начиная с момента начала стока (см. рис. 31.3), вычисляют интенсивность ливня a _i = D H_j /D t_j и интенсивность впитывания b_i = D P_j /D t_j;

отыскивают значения боковой приточности, применяя уравнение (31.2) последовательно сверху вниз для каждой пары створов каждого i -го бокового лога, начиная от водораздела;

находят сосредоточенные расходы в устьевых створах каждого i -го бокового лога, решая систему уравнений (31.4-31.5) последовательно для каждой пары створов вниз по тальвегу, начиная с водораздела;

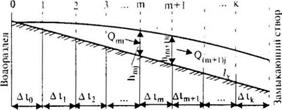
Рис. 31.6. Схема деления главного лога на расчетные интервалы длины D l_m

строят эпюру боковой приточности главного лога, представляемую в виде кусочно-постоянной функции (см. рис. 31.2);

отыскивают значение расхода в замыкающем створе главного лога для первого интервала времени, решая систему уравнений (31.4-31.5) последовательно для каждой пары створов сверху вниз по тальвегу;

затем те же операции выполняют для второго интервала времени с учетом уже вычисленных за предшествующий период времени объемов стока на склонах и в логах и т.д.

На основе изложенного алгоритма канд. техн. наук И.В. Чистяковым в 1983 году разработана программа «STOK» для детального расчета ливневого стока с малых водосборов. Применение этой методики дает в ряде случаев возможность уменьшить расходы на строительство и эксплуатацию малых мостов и труб до 20 %.

Конечным итогом детального компьютерного расчета стока ливневых вод с малых водосборов является получение расчетного гидрографа ливневого стока в замыкающем створе водосбора Q = f (t), используемого в дальнейшем для расчетов отверстий малых водопропускных сооружений на автомобильных дорогах с учетом аккумуляции. Однако в случае необходимости может быть получена и другая информация, которая может интересовать инженера-дорожника: скорости течения, глубины и уровни воды, кривые свободной поверхности воды вдоль лога и т.д. на любой момент паводка.

Для дальнейших расчетов отверстий малых водопропускных сооружений по полученным расчетным гидрографам стока Q = f (t), в конечном итоге необходимо определять следующие величины:

максимальный расход ливневых вод, м³/с;

объем стока ливневых вод, м³;

длительность паводка, мин;

относительное время подъема паводка, мин;

полноту гидрографа расчетного паводка.

Дата добавления: 2015-06-04