Математическое моделирование стока талых вод с малых водосборов

До недавнего времени при проектировании малых водопропускных сооружений аккумуляцию талых вод не учитывали (хотя это явление почти всегда имеет место), что в ряде случаев приводило к назначению завышенных размеров отверстий сооружений и геодезических высот бровок земляного полотна над ними. Это было связано, во-первых, с отсутствием надежных методов расчета объемов стока талых вод и, во-вторых, с неверным представлением о форме и продолжительности гидрографа стока в форме одно-модальной трапеции, которая справедлива только для водосборов площадью более 200 км². Для малых же водосборов гидрограф стока талых вод имеет выраженный внутри суточный ход, причем, максимальные расходы превосходят минимальные в 5-10 раз, что приводит к образованию кратковременного пруда аккумуляции талых вод в периоды дневного стока с последующим его сбросом в периоды ночного минимума.

Современные представления о механизме формирования стока талых вод состоят в следующем:

в результате таяния снега в верхнем его слое жидкость частично удерживается абсорбционными и капиллярными факторами, заполняя, так называемую, водоудерживающую емкость снега и частично проникает в более глубокие слои, постепенно насыщая всю толщу снега, вплоть до подстилающего грунта;

оставшаяся вода стекает вдоль склонов водосборов и затем попадает в русловую сеть тальвегов. Со временем сюда же попадает и часть воды, которая передвигалась вдоль склонов по временным и постоянным водоупорам;

в ходе этого процесса некоторая часть воды испаряется, а некоторая продолжает просачиваться в более глубокие слои почв;

процесс отекания талой воды по склонам при наличии снега качественно отличается от склонового стока ливневых вод. Только после попадания в русловую сеть тальвегов его пропуск аналогичен пропуску ливневого стока.

При формировании талого стока выделяют два основных случая:

талый сток по не промерзшей почве. В этом случае интенсивность впитывания в почву лишь немногим меньше интенсивности снеготаяния и водоотдачи из снега, поэтому сток талых вод незначителен;

талый сток по промерзшей почве. В этом случае почва представляет собой водоупор, по которому происходит склоновый сток талых вод в водонасыщенных слоях снега с последующим попаданием его в русловую сеть тальвегов. Этот случай более опасен, поскольку здесь объемы и максимальные расходы снегового стока могут достигать значительных величин.

В суточных изменениях гидротермического режима таящего снега выделяют 4 основные фазы:

утреннее прогревание слоя снега до температуры таяния;

дневное снеготаяние (пик приходится примерно на 13-14 часов);

вечернее охлаждение поверхности снега;

ночное промерзание (когда температура снега опускается ниже 0°С, талая вода замерзает, склоновый сток прекращается).

Главными факторами, требующими учета при расчетах аккумуляции талой воды перед сооружениями, являются уклоны склонов и русла, их шероховатости и экспозиция водосбора относительно стран света.

Аккумуляция возникает, когда есть стеснение потока. Однако при принятии трапецеидальной формы гидрографа притока с значительной продолжительностью максимального расхода, сбросный расход в сооружении может достичь величины максимального расхода притока только при больших бассейнах (рис. 31.7, а). Для малых же водосборов с выраженным внутрисуточным ходом стока время притока максимального расхода к сооружению недостаточно для уравнивания расходов, что вызывает снижение сбросных расходов по сравнению с максимальными расходами притока (рис. 31.7, б, в). На малом водосборе могут формироваться до 2-3 примерно одинаковых суточных максимума стока, при этом время интенсивного стока составляет около 10 часов в сутки. Поэтому накопленный во время дневного максимума притока пруд аккумуляции талой воды должен быть опорожнен до начала подъема паводка следующих суток.

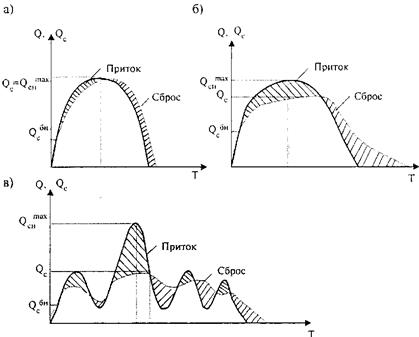
Рис. 31.7. Типы взаимодействия между гидрографами притока и сброса талых вод

Основными генетическими факторами образования стока талых вод являются мощность снежного покрова к началу таяния и максимальные суточные величины радиационного баланса границы «снег-атмосфера».

Максимальный расход неуклонно возрастает при изменении высоты снежного покрова от 15 до 60 см, а затем замедляется и в пределе полностью стабилизируется (в этом случае гидрограф стока растягивается во времени).

С увеличением же радиационного баланса резко возрастают максимумы расхода и суточного объема снегового стока (при этом период снеготаяния уменьшается, а гидрограф стока сокращается во времени).

Таким образом, с точки зрения возможных разрушений водопропускных сооружений наиболее опасными являются половодья, происходящие при наибольших суточных максимумах радиационного баланса, если начальная мощность снежного покрова достаточно велика.

При схематизации гидрографа притока и сброса талых вод треугольниками в ходе 24 часового суточного цикла максимальный сбросный расход имеет следующий вид:

где

Q_c - максимальный сбросный расход в сооружении;

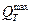- максимальный расход притока талой воды.

Это означает, что предельное снижение расчетных сбросных расходов не должно превышать в 2,4 раза по сравнению с максимальным расходом притока. С некоторым гарантийным запасом эту величину уменьшают до 2-х. Тогда система ограничений для назначения отверстий малых водопропускных сооружений примет вид:

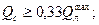
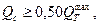где

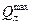- максимальный ливневый расход.

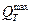- максимальный расход талых вод.

Интенсивность поступления воды на водосбор в период таяния снега зависит от величины снегозапасов, физических свойств снега и количества тепла, поступающего из атмосферы к верхней границе снегового покрова.

Основными составляющими потока тепла на поверхности снежного покрова являются: прямая и рассеянная коротковолновая радиация, длинноволновое излучение из атмосферы и снега, турбулентный теплообмен атмосферы и снега, теплообмен при конденсации и испарении снега, поступление тепла вместе с жидкими осадками. Поток тепла из почвы определяется ее температурой и физическими свойствами, в частности, тепло- и температуропроводимостью.

Гидротермодинамический режим снежного покрова описывают системой дифференциальных уравнений, предложенных Л.С. Кучментом:

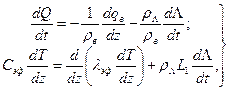где (31.6)

Q - объемная влажность снега в долях единицы;

t - время;

r_в, r_L - плотности воды и льда;

q_в - поток влаги по вертикали;

z - расстояние по вертикали;

L - объемная льдистость снега в долях единицы;

С_эф - эффективный коэффициент теплоемкости снега;

Т - температура снега;

l_эф - эффективный коэффициент теплопроводимости снега;

L ₁ - удельная теплота плавления льда.

С_эф и l_эф определяют по следующим формулам:

С_эф = С _L · r_L · L + С_в · r_в · Q;

l_эф = 0,00005 + 0,004 r_с ² где

С _L и С_в - теплоемкости льда и воды;

r_с - плотность снега.

С _L, С_в, r_в, r_L, r_с и другие гидрофизические константы для расчета талых вод приведены в табл. 31.2.

Таблица 31.2.

Гидрофизические константы для расчета талых вод

№, п/п	Наименование константы	Обозначение	Числовое значение	Размерность
	Плотность воды	rв	1,0	г/см^3
	Плотность льда	rL	0,917	г/см^3
	Теплоемкость воды	Св	1,0	кал/г.град
	Теплоемкость льда	С L	0,5	кал/г.град
	Удельная теплота плавления льда	L 1	80,0	кал/г
	Удельная теплота возгонки льда	L 3	680,0	кал/г
	Константа Стефана-Больцмана	s	8,16·10^-11	кал/(см^2.мин.град)
	Альбедо снега	rc	0,8305	безразмерно

Система уравнений (31.6) описывает гидротермодинамический режим снега как трехфазной среды, состоящей из льда, жидкой воды и воздуха (пара). Систему (31.6) решают в конечных разностях. В качестве исходной метеорологической информации используют данные о ходе радиационного баланса границы «снег-атмосфера» (приток или отток тепла) и мощности снежного покрова к началу таяния. Необходимые метеорологические данные можно получить из климатических справочников рассматриваемых районов.

Для расчета гидротермического режима снега его общую толщину разбивают на N слоев толщиной D z и аппроксимируют системой уравнений (31.6) в конечноразностной форме:

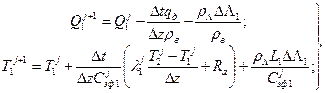
граница снег-атмосфера

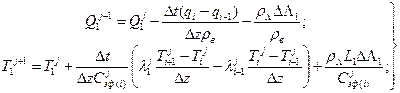
граница снег-почва

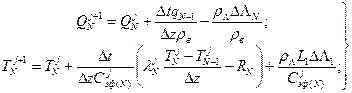где

j - индекс шага (интервала) по времени t;

i - индекс шага (интервала) по вертикали z;

q_д - поток влаги от жидких осадков;

R_a - поток тепла из атмосферы;

R_N - поток тепла в почву.

Поток влаги из верхнего расчетного слоя снега в нижний определяется водоудерживающей способностью снега

q_{i +1} = r_в (Q_i - Q_вc)D z /D t при Q_i > Q_вc;

q_{i +1} = 0 при Q_i £ Q_вc, где

Q_вc - водоудерживающая способность снега, рассчитываемая по формуле:

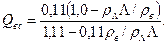
Количество тепла, необходимое для того, чтобы за время D t повысить температуру единичного объема снега до 0° С

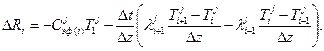
Величина D R_i представляет собой «эффективный запас холода» элемента снега, который слагается из теплосодержания элемента и разности потоков тепла к нему за время D t. D R_i может компенсироваться за счет образования и таяния льда:

D L _{( i )max} = D R_i / r_LL ₁.

Так как температура снега всегда ниже 0° С, то внутри снежного покрова происходит только процесс образования льда. Увеличение льдистости за время D t находят из соотношений:

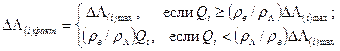
Для поверхностного слоя снега запас холода находят из выражения:

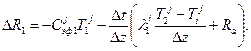
а для нижнего слоя

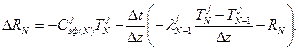
При таянии снега с поверхности (т.е. при D R ₁ <0) высота верхнего расчетного слоя уменьшается на величину

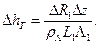
Приращение влажности в верхнем слое определяют по воднобалансовому уравнению:

Изменение льдистости на таящей поверхности

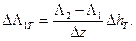
Распределение плотности сухого снега

r_с = 0,1695 + 0,0037 z.

Распределение температуры в толще снега в начальный момент времени вычисляют по линейной формуле:

Т_ci = Т_{с 1} - (Т_{с 1} - Т_n) z, где

Т_n - температура почвы.

Величину радиационного баланса границы «снег-атмосфера» задают по материалам климатических справочников, а при их отсутствии определяют по методике П.П. Кузьмина:

R_R = R ₀ (1 - r_c) (1 - 0,1 N ₀ - 0,47 N_н), где

R_R - поток прямой коротковолновой радиации;

R ₀ - максимально возможная интенсивность суммарной коротковолновой радиации при безоблачном небе;

r_c - альбедо снега;

N ₀ и N_н - общая и нижняя облачность в долях единицы.

Величину R ₀ оценивают по приближенной зависимости:

R ₀ = 0,025 h ₀, где

h ₀ - высота солнца над горизонтом в градусах, определяемая по уравнению:

sin h ₀ = sin j sin d + cos j cos d cos w, где

j - географическая широта местности;

d и w - склонение и часовой угол Солнца, определяемые по формулам:

d = 23,5 sin(2 p)(t_c - 81)/ П; w = p (t_ч - 12)/12, где

П - количество дней в году;

t_c - время в сутках от 1 января;

t_ч - местное время в часах от полуночи.

Альбедо снежного покрова зависит от структуры и влажности поверхностного слоя снега. Интегральной характеристикой этих величин считают плотность поверхностного слоя снега r_сi.

При r_сi > 0,1 г/см³ альбедо снежного покрова вычисляют по формуле:

r_c = 1,03 - r_сi.

Расчет длинноволнового излучения атмосферы производят по формуле:

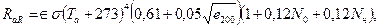где

Î - относительная поглащательная способность длинноволновой радиации;

s - константа Стефана-Больцмана (см. табл. 31.2);

Т_а - температура воздуха;

е ₂₀₀ - упругость водяного пара.

Расчет длинноволнового излучения снега выполняют по формуле:

где

Т_пов - температура поверхности снега.

Турбулентный теплообмен атмосферы и снега определяют по формуле:

R_Т = 1,75(Т_а - Т_пов)(0,18 + 0,098 U)·0,027, где

U - скорость ветра, м/с.

Расчет затрат тепла на испарение снега выполняют по формуле:

R_и = 1,75 (е ₂₀₀ - е_с)(0,18 + 0,098 U)·0,027, где

е_с - максимальная упругость водяного пара надо льдом при температуре Т_пов, которая равна

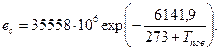
Поток тепла от выпадения жидких осадков

R_ос = r_вС_вT_аR_ж, где

R_ж - интенсивность жидких осадков.

Окончательно радиационный баланс границы «снег-атмосфера» равен

R_а = R_R + R_аR + R_T - R_и - R_CR + R_oc

Поток тепла в почву задают по приближенной формуле:

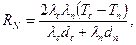где

l_с, l_п - теплопроводимости снега и почвы;

T_с, T_п - температуры нижнего слоя снега и почвы;

d_с, d_п - толщины нижнего слоя снега и расчетного слоя почвы (для приблизительных расчетов допускают d_с = d_п).

Допуская, что теплопроводимость промерзшей минеральной почвы примерно в 10 раз больше теплопроводи мости снега, а ее температура остается постоянной за период таяния и равна -1°С, для задания потока тепла в почву используют формулу:

R_N = 1,8 l_с (T_с + 1), где

l_с, T_с - теплопроводимость и температура нижнего слоя снега.

Для описания склонового стока талых вод используют уравнение кинематической волны в следующем ви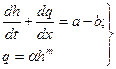де:

где

h - глубина потока, м;

t - время, сек;

q - приток воды в единицу времени на единицу длины склона, м³/(см);

х - расстояние по рассматриваемому направлению склона, м;

а - поступление воды, м/с;

b - потери, м/с;

a, m - множитель и показатель степени, которые: для ламинарного движения a = gi_c /2 v и m = 3, для турбулентных 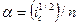и m =5/3;

i_c - уклон склона, ‰;

п - коэффициент Маннинга;

v - кинематическая вязкость.

Преобразуя для описания склонового стока талой воды в водонасыщенных слоях снега, уравнение кинематической волны представляют в виде:

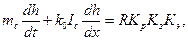где (31.7)

m_c - пористость снега (m_c = 1 - L - Q_c);

L - льдистость снега;

Q_c - влажность снега;

k ₀ = 64,5ехр(-7, 8r_с) - коэффициент гидравлической проводимости водонасыщенного снега;

I_c - уклон склона (при углах наклона поверхности склона j_с = 1-15° sin j_с» I_c);

r_с - плотность снега, г/см³;

R - избыток (дефицит) влаги в снеге относительно водоудерживающей способности склона;

K_p = 1 - 0,8 l_g (1 + 0,1 f_б + 0,05 f_L) - коэффициент, учитывающий перехват талых вод растительностью, заболоченными участками водосбора;

f_б, f_L - средневзвешенная заболоченность и залесенность рассматриваемого склона (правого и левого).

К_з = 0,9(F - F_з)/ F - коэффициент потерь на заполнение углублений;

F, F_з - соответственно площадь водосбора и площадь углублений, ограниченная замкнутыми горизонталями внутри бассейна;

К_э - коэффициент экспозиции относительно стран света:

К_э = 1,0 при экспозиции 3, В;

К_э = 0,8 - 1,0 при экспозиции С;

К_э = 1,0 - 1,2 при экспозиции Ю.

Если глубина талой воды превысит мощность снежного покрова или стекание по склонам происходит на полностью очистившихся склонах, то уравнение кинематической волны представляют в следующем виде:

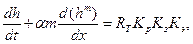где (31.8)

m = 5/3; ;

R_T - приток влаги от таяния последнего слоя снега.

Для решения уравнений (31.7) и (31.8) применяют следующие 2 способа схематизации водосборных бассейнов:

1. Водосбор в виде конической поверхности, сходящейся к замкнутому створу (рис. 31.8, а) - для схематизации пологих и широких водосборов, имеющих плавную, близкую к сектору окружности, конфигурацию.

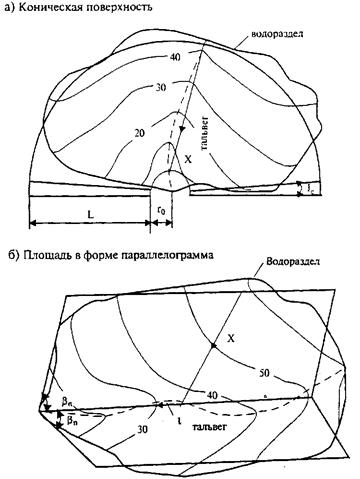
Рис. 31.8. Способы схематизации водосборных бассейнов

В этом случае формулы (31.7) и (31.8) представляют в следующем виде:

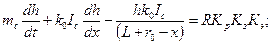(31.9)

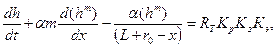(31.10)

где слагаемые

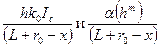
представляют собой увеличение глубин талой воды за счет схождения водораздела к замыкающему створу;

L - радиус схематизации водосбора;

r ₀ - ширина замыкающего створа;

х - текущая координата по расстоянию.

При этой схематизации нет нужды производить расчет руслового стока талых вод в главном тальвеге, т.к. параметры потока талых вод в замыкающем створе определяются уже после решения одного из уравнений (31.9) и (31.10).

2. Водосбор в виде 2-х площадок, имеющих форму параллелограммов и примыкающих к главному тальвегу под углами, которые составляют направления средних уклонов склонов бассейна (рис. 31.8, б), при этом для каждой площади задают свои уклоны, коэффициенты шероховатости, потери, экспозиции и размеры. Этот способ более универсален и может быть использован для схематизации водосборов любой формы.

При обоих способах схематизированные бассейны по площади должны соответствовать реальным.

Решение уравнений (31.9-31.10) производят следующим образом: на склоне выбирают полосу единичной ширины, на которой разбивается конечно-разностная схема с шагом по расстоянию 20-200 м (в зависимости от длины склона), а шаг по времени выбирают, исходя из продолжительности весеннего снеготаяния (как правило, шаг по времени принимают равным шагу, принятому в расчетах гидротермического режима снега).

Аппроксимируя дифференциальные уравнения (31.9-31.10) по разностной схеме, получают:

1. Для схематизации в виде конической поверхности

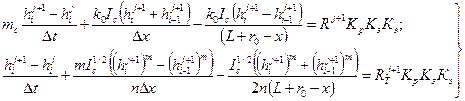(31.11)

2. Для схематизации в виде площадок

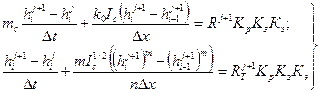(31.12)

i - индекс по интервалу расстояния;

j - индекс по интервалу времени.

За граничные условия для решения уравнений (31.11) и (31.12) принимают глубины на первой расчетной вертикали при всех интервалах времени и на всех расчетных вертикалях в первый момент времени.

Решая уравнения в замыкающем створе водосбора, схематизированного в виде конической поверхности, определяют глубины талых вод, после чего по формулам для водослива с широким порогом рассчитывают скорость n и расход потока Q в этом створе:

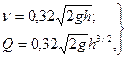где

h - глубина потока, м;

g - ускорение силы тяжести, м/с².

Полный объем стока талых вод и объем за любые дискретные интервалы времени можно определить по рекуррентной формуле:

W = W + Q D t.

Для водосбора в виде площадок на последних расчетных вертикалях определяют величины бокового притока и скорости по формулам:

q_б = n_б (h_п + h_л);

V_б = 0,45g^1/2((h_п)^1/2cos b_п + (h_л)^1/2cos b_л), где (31.13)

q_б - величина бокового притока талой воды в тальвег в единицу времени на единицу его длины, м³/(с.м);

V_б - проекция скорости бокового притока на оси тальвега, м/с;

h_п, h_л - соответственно глубина талой воды на последних расчетных створах правой и левой площадок к тальвегу, м;

b_п, b_л - углы примыкания правой и левой площадок к тальвегу.

Для описания движения талых вод в руслах непризматической формы с переменной боковой приточностью применяют следующую систему уравнений неустановившегося движения жидкости:

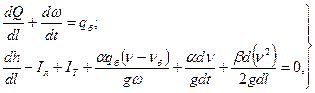где (31.14)

Q - расход воды в русле, м/с;

w - площадь живого сечения потока, м²;

l - длина рассматриваемого участка по тальвегу, м;

t - время;

q_б - боковой приток в тальвег в единицу времени на единицу длины, м³/(с.м);

h - глубина потока в русле, м;

I_л - уклон дна лога, ‰;

I_T - уклон трения;

a - коэффициент Кориолиса (как правило, a = 1,1);

V - скорость потока в русле, м/с;

n_б - проекция скорости бокового притока на ось русла, м/с;

g - ускорение свободного падения;

b - коэффициент Буссинеска.

Уклон трения при установившемся состоянии потока допускают определять на основе формулы Маннинга:

I_T = (Q ² п ² Р ^4/3)/ w ^10/3, где

п - коэффициент шероховатости русла (табл. 31.3);

Р - смоченный периметр сечения.

Таблица 31.3.

Коэффициенты шероховатости для открытых русел

Тип русла и его описание	Коэффициент шероховатости
Искусственные земляные или гладкие из скальных обломков	0,016-0,025
Естественные небольшие, максимальной шириной до 30 м, чистые и прямые	0,025-0,033
Земляные русла периодических водотоков	0,033 - 0,040
Поймы травянистые	0,040 - 0,050
Поймы кустарниковые	0,050 - 0,070

Решение системы уравнений (31.14) производят методом конечных разностей:

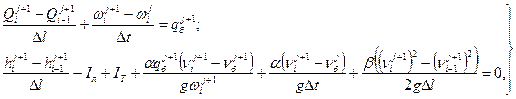(31.15)

Для определения площади живого сечения w и смоченного периметра Р поперечный профиль русла схематизируют семью точками (рис. 31.9), при этом считают, что поперечный профиль одинаков по всей длине русла. Тогда площадь поперечного сечения равна

w = 1/2[(X₁ - Х₂)(Y₁ - Y₂) + (Х₂ - Х₃)(Y₂ + Y₃) +... + (Х_n - Х_n)(Y_n + Y_n)], где

n - общее количество координат (в данном случае n = 7);

X₁... _n, Y₁... _n - прямоугольные координаты точек, зависящие от глубины потока в русле схематизированного поперечного сечения русла.

В результате решения уравнений (31.15) получают глубину, скорость и расход потока талых вод во входном створе проектируемого искусственного сооружения по заданным интервалам времени. Это дает возможность получить гидрограф стока, определить его полный объем и объемы за различные интервалы времени (например, за сутки) и тем самым решить следующее уравнение сбросных расходов для предварительно назначенных вариантов искусственного сооружения:

dW_np = Qdt - Q_cdt, где

W_np - объем пруда, тыс.м³;

Q - расход притока у входа сооружения, м³/с;

Q_c - сбросный расход в сооружении, м³/с.

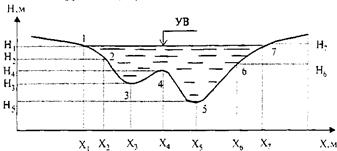
Рис. 31.9. Схема поперечного профиля русла

Необходимо отметить, что снижение сбросных расходов в сооружениях допускается не более чем в 3 раза по сравнению с максимальным расходом притока.

При упрощенной схематизации гидрографа в виде равновеликого по площади треугольника расхождение сбросного расхода не составляет более 10 %.

На основе приведенных теоретических предпосылок д-ром техн. наук К.Н. Макаровым разработана единая физико-математическая модель для расчета снегового стока с малых водосборов, состоящая из следующих трех частей:

моделирования гидротермодинамического режима таящего снежного покрова и водоотдачи из снега;

моделирования снегового стока талых вод в водонасыщенных слоях снега и при отсутствии снега;

моделирования руслового стока талых вод по тальвегу водосбора.

Изложенная выше математическая модель стока талых вод с малых водосборов реализована по следующему алгоритму:

задают начальное значение мощности снежного покрова и число слоев разбиения с учетом ВП (табл. 31.4-31.5);

Таблица 31.4.

Вероятные высоты снежного покрова к началу таяния, осредненные по УГКС, см.

УТКС	Вероятность превышения, %
поле	лес	поле	лес	поле	лес	поле	лес
Мурманское
Северное
Северо-Западное
Уральское
Эстонское	-	-
Латвийское	-	-
Литовское	-	-
Белорусское
Верхне - Волжское
Приволжское
Центр.-Черноземное
Украинское	-	-
Северо- Кавказское	-	-
Омское
Западно-Сибирское	-	-
Казахское	-	-		-		-		-
Красноярское
Якутское	-	-
Иркутское
Забайкальское	-	-
Колымское
Дальне-Восточное
Приморское	-	-
Камчатское
Сахалинское

Таблица 31.5.

Вероятности превышения основных стокообразующих факторов в зависимости от категории дорог

Категории дороги	ВП паводка, %	ВП высоты снега. %	ВП радиационного баланса. %
-	0?1
I
II-III
IV-V

с определенным шагом по времени задают или рассчитывают по соответствующим формулам радиационный баланс границы «снег-атмосфера»;

для каждого расчетного интервала времени и каждого слоя снега рассчитывают значения температуры и влажности, а также величину слоя спаивания снега с поверхности;

для каждого интервала времени вычисляют величину избытка или дефицита влаги в нижнем слое снега относительно его водоудерживающей способности;

для каждого интервала времени решают уравнение склонового стока талых вод в водонасыщенном слое снега или при отсутствии снега и определяют величину и скорость бокового притока со склонов в русло;

решают систему уравнений руслового стока и определяют для каждого интервала времени значения глубины, скорости и расхода потока талых вод в замыкающем створе водосбора.

Изложенный алгоритм расчета стока талых вод с малых водосборов реализован К.Н. Макаровым в виде расчетной программы «СНЕГ». Программа позволяет с заданным шагом по времени от 1 до 6 часовой продолжительности рассчитывать бытовые значения глубины, скорости и расхода потока талых вод в замыкающем створе водосбора. В программе предусмотрено 3 варианта задания исходных данных о радиационном балансе границы «снег-атмосфера», 2 способа схематизации водосборных бассейнов и 2 варианта выдачи результатов.

Экономическая эффективность учета аккумуляции талых вод за счет уменьшения размеров отверстий водопропускных сооружений на автомобильных дорогах в отдельных случаях может достигать до 48 % от суммарной стоимости тела трубы и укреплений.

По результатам массовых расчетов с использованием программы «СНЕГ» К.Н. Макаровым составлены таблицы модуля объема снегового стока с 1 км² за сутки с ВП = 1 % для Европейской и Азиатской территорий России в зависимости от географической широты места и плошали водосбора (табл. 31.6). Для расчетов использовались водосборы от 1 до 120 км² со средними уклонами лога 0,015 и склонов 0,020. В качестве исходных использованы данные о высоте снежного покрова (см. табл. 31.4) и радиационном балансе границы «снег-атмосфера» (табл. 31.7) по климатическим справочникам Гидрометеоиздата.

Таблица 31.6.

Модуль объема снегового стока, 1000 м³/сут.

Широта места (°)	Площадь водосбора, км^2
0,0-2,0	2,0-5,0	5,0-10,0	10,01-20,00	20,01-30,00	30,01-50,00	50,01-100,00	более 100
Для Европейской части России
65-70	38,54	32,96	25,43	24,63	23,28	21,43	21,14	20,98
60-64	45,16	38,83	30,06	29,42	27,71	25,69	25,40	25,20
56-59	51,81	44,03	37,20	34,67	34,59	32,16	31,93	30,41
52-55	56,06	51,26	39,22	38,16	35,83	33,48	31,30	30,78
48-51	49,09	41,96	32,28	31,36	29,57	27,24	25,39	25,22
44-47	28,72	24,43	18,56	17,92	16,82	15,26	12,71	7,69
40-43	15,55	13,41	10,49	10,22	9,89	9,09	8,82	8,51
Для Азиатской части России
72-76	38,52	38,47	35,56	34,14	33,34	32,92	30,83	18,19
68-71	46,41	39,61	30,46	29,63	27,88	25,65	25,30	21,65
64-67	27,61	23,50	18,26	17,67	17,61	15,47	15,38	14,32
60-63	30,69	26,12	20,30	19,68	18,61	17,09	16,01	15,30
56-59	46,50	39,62	30,77	29,97	28,47	26,28	25,58	23,34
52-55	46,64	39,82	30,79	30,09	28,73	26,24	25,90	21,40
48-51	27,61	23,45	18,44	17,92	17,33	17,01	15,70	11,98
44-47	27.76	25.29	23,84	23.90	23,80	23.05	23,02	17.31

Таблица 31.7.

Максимумы и минимумы радиационного баланса границы "снег-атмосфера"

Широта места	Минимумы кал/см\мин	Максимумы кал/см^2.мин
ETC	АТС	ETC	АТС
	-	0,01	-	0,31
	-	0,00	-	0,53
	-	-0,02	-	0,64
	-0,08	-0,07	0,67	0,67
	-0,08	-0,08	0,66	0,56
	-0,08	-0,08	0,72	0,70
	-0,08	-0,08	0,76	0,76
	-0,08	-0,08	0,70	0,68
	-0,08	-0,08	0,75	0,72
	-0,08	-0,08	0,80	0,74
	-0,08	-0,09	0,85	0,76

Расчет снегового стока с малых водосборов по упрошенной методике производят в следующей последовательности:

1. Определяют максимальный суточный объем стока за половодье по формуле:

W_CT = lW ₁ FK_pK_э ×10³, где

W_CT - максимальный суточный объем, м³ снегового стока заданной ВП;

l - коэффициент перехода от модуля объема стока с ВП = 1 % к модулю объема стока заданной ВП, определяемый по табл. 31.8;

Таблица 31.8.

Значения переходного коэффициента l

ВП %	0,1
l	1,70	1,00	0,85	0,78

W ₁ - модуль объема снегового стока с 1 км² с ВП = 1 %, тыс. м³, определяемый по табл. 31.6 в зависимости от площади и местонахождения водосбора;

F - площадь водосбора, км²;

K_э - коэффициент экспозиции водосбора относительно стран света;

K_p - коэффициент перехвата талых вод растительностью и болотами, рассчитываемый по формуле:

K_p = 1 - 0,81g(1 + 0,1 f_б + 0,05 f_л), где

f_б, f_л - средневзвешенная заболоченность и залесенность рассматриваемого склона (правого и левого).

Если принять b = 1+ 0,1 f_б + 0,05 f_л, то b и K_p имеют соотношение:

b................................... 2 3 4 5 6 7 8

K_p................................. 0,76 0,62 0,54 0,44 0,38 0,32 0,28

2. В зависимости от площади водосбора рассчитывают максимальный расход талых вод заданной ВП следующими двумя способами:

а) при F £ 20 км² - гидрограф стока схематизируют в виде треугольника, а продолжительность интенсивного стока принимают равной 10 час, тогда

где

Т_сп - продолжительность снегового паводка за сутки (Т_сп = 10 час);

б) при F >20 км² - гидрограф стока схематизируют в виде параболы, а время интенсивного стока принимают в среднем 14 час, тогда

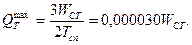
3. Для назначения отверстия сооружения с учетом аккумуляции талых вод на графике водопропускной способности труб (рис. 31.10), построенном в координатах Н ³ и Q_тр (где Н - подпор перед трубой, Q_тр - расход в трубе), строят отрезок прямой сбросных расходов с координатами: Н ³ = 0,85 W_CT / a и 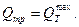Здесь

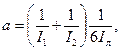где (31.16)

I ₁, I ₂ - уклоны склонов водосбора, ‰;

I_л - уклон лога, ‰.

4. На графике из точки 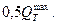восстанавливают перпендикуляр к оси абсцисс, который разделит плоскость чертежа на 2 зоны (см. рис. 31.10). Точки пересечения отрезка прямой сбросных расходов с кривыми пропускной способности труб, лежащие справа от пересечения этой прямой с перпендикуляром к оси абсцисс, дают искомые значения расхода и подпора для соответствующих типоразмеров труб.

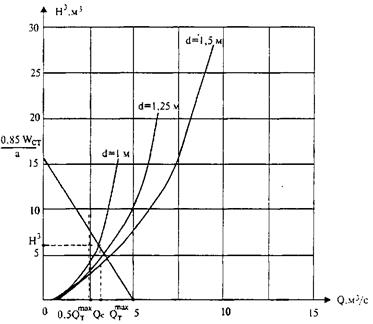
Рис. 31.10. Графическое построение для определения отверстия сооружения с учетом аккумуляции талых вод

Пример. Дано: l = 0,85 (табл. 31.8); W ₁ = 44,03 тыс. м³ (табл. 31.6); F= 2,33 км²; К_р =1 (т. к. лес может быть вырублен за срок эксплуатации); К_э = 1 (восточная экспозиция); I ₁= 0,011, I ₂ = 0,012, I_л = 0,006. Определить 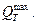и выбрать типоразмер трубы с учетом аккумуляции.

W_CT = lW ₁ FK_pK_э ×10³ = 0,85×44,03×2,33×1,1×1000 = 87201,42 м³.

Поскольку площадь водосбора менее 20 км², то

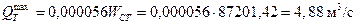
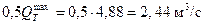
Для пропуска расхода 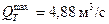без учета аккумуляции может быть запроектирована труба круглого сечения диаметром 1,5 м, пропускающая данный расход при подпоре 1,78 м и скорости на выходе 3,70 м/с. Однако, если рельеф водосбора допускает создание значительного по объему пруда аккумуляции, то производят расчет отверстия трубы с учетом аккумуляции талых вод. Для этого определяют величину а по формуле (31.16), принимая I ₁= 0,011, I ₂ = 0,012, I_л = 0,006, т.е. а = 4839,8, и координаты отрезка прямой сбросных расходов:

Н ³ = 0,85 W_CT / a = 15,3 м³; ;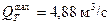

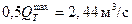
Произведя необходимые графические построения (см. рис. 31.10), можно принимать круглую трубу d =1,0 м, для которой сбросный расход Q_c = 3,05 м³/с и Н ³ = 5,9 м³. Следовательно, подпор составляет (5,9)^1/3 =1,81 м, а скорость на выходе трубы v = 4,10 м/с.

По изложенному упрощенному методу расчета расхождение по сравнению с результатами компьютерных расчетов составляет:

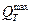
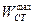
Для............................... 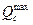Н скорости на выходе

До, %........................... 15 % 5 % 10 % 5 % 3 %

Дата добавления: 2015-06-04