Способы табличного и графического представления результатов эксперимента 2 страница

Часть II. Введение в научное психологическое исследование

случае степенью свободы будет число, равное и — 2, где п — ко­личество данных в коррелируемых рядах.) Заметим, что значи­мость коэффициента корреляции зависит и от заданного уров­ня значимости или принятой вероятности допустимой ошибки в расчетах. Если, к примеру, коррелируется друг с другом два ря­да цифр по 10 единиц в каждом и получен коэффициент корре­ляции между ними, равный 0,65, то он будет значимым на уров­не 0,95 (он больше критического табличного значения, состав­ляющего 0,6319 для вероятности допустимой ошибки 0,05, и меньше критического значения 0,7646 для вероятности допусти­мой ошибки 0,01).

Метод множественных корреляций в отличие от метода пар­ных корреляций позволяет выявить общую структуру корреля­ционных зависимостей, существующих внутри многомерного экспериментального материала, включающего более двух пере­менных, и представить эти корреляционные зависимости в виде некоторой системы.

Один из наиболее распространенных вариантов этого мето­да — факторный анализ — позволяет определить совокупность внутренних взаимосвязей, возможных причинно-следственных связей, существующих в экспериментальном материале. В ре­зультате факторного анализа обнаруживаются так называемые факторы — причины, объясняющие множество частных (пар­ных) корреляционных зависимостей.

Фактор — математико-статистическое понятие. Будучи пере­веденным на язык психологии (эта процедура называется содер­жательной или психологической интерпретацией факторов), он становится психологическим понятием. Например, в известном 16-факторном личностном тесте Р. Кеттела, который подробно рас­сматривался в первой части книги, каждый фактор взаимно одно­значно связан с определенными чертами личности человека.

С помощью выявленных факторов объясняют взаимозави-. симость психологических явлений. Поясним сказанное на при­мере. Допустим, что в некотором психолого-педагогическом экс­перименте изучалось взаимовлияние таких переменных, как ха­рактер, способности, потребности и успеваемость учащихся. Предположим далее, что, оценив каждую из этих переменных у

Глава 3. Статистический анализ экспериментальных данных

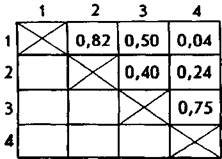
достаточно представительной выборки испытуемых и подсчитав коэффициенты парных корреляций между всевозможными па­рами данных переменных, мы получили следующую матрицу ин­теркорреляций (в ней справа и сверху цифрами обозначены в пе­речисленном выше порядке изученные в эксперименте перемен­ные, а внутри самого квадрата показаны их корреляции друг с другом; поскольку всевозможных пар в данном случае меньше, чем клеток в матрице, то заполнена только верхняя часть матри­цы, расположенная выше ее главной диагонали).

Анализ корреляционной матрицы показывает, что пе­ременная 1 (характер) значи­мо коррелирует с переменны­ми 2 и 3 (способности и по­требности). Переменная 2 (способности) достоверно коррелирует с переменной 3 (потребности), а переменная 3 (потребности) — с перемен­ной 4 (успеваемость). Факти­чески из шести имеющихся в матрице коэффициентов корреля­ции четыре являются достаточно высокими и, если предполо­жить, что они определялись на совокупности испытуемых, пре­вышающей 10 человек, — значимыми.

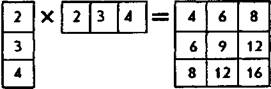
Зададим некоторое правило умножения столбцов цифр на стро­ки матрицы: каждая цифра столбца последовательно умножается на каждую цифру строки и результаты парных произведений за­писываются в строку аналогичной матрицы. Пример: если по это­му правилу умножить друг на друга три цифры столбца и строки, представленные в левой части матричного равенства, то получим матрицу, находящуюся в правой части этого же равенства:

Часть II. Введение в научное психологическое исследование

Задача факторного анализа по отношению к только что рас­смотренной является как бы противоположной. Она сводится к тому, чтобы по уже имеющейся матрице парных корреляций, ана­логичной представленной в правой части показанного выше мат­ричного равенства, отыскать одинаковые по включенным в них цифрам столбец и строку, умножение которых друг на друга по заданному правилу порождает корреляционную матрицу. Иллю­страция:

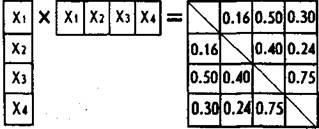
Здесь x_v х_у х₃ и х_А — искомые числа. Для их точного и быст­рого определения существуют специальные математические про­цедуры и программы для ЭВМ.

Допустим, что мы уже нашли эти цифры: х_х = 0,45, х₂= 0,36 х₃ - 1,12, х₄ = 0,67. Совокупность найденных цифр и называется фактором, а сами эти цифры — факторными весами или нагруз­ками.

Эти цифры соответствуют тем психологическим переменным, между которыми вычислялись парные корреляции. х_х — харак­тер, х₂ — способности, х₃ — потребности, х₄ — успеваемость. По­скольку наблюдаемые в эксперименте корреляции между пере­менными можно рассматривать как следствие влияния на них общих причин — факторов, а факторы интерпретируются в пси­хологических терминах, мы можем теперь от факторов перейти к содержательной психологической интерпретации обнаружен­ных статистических закономерностей. Фактор содержит в себе ту же самую информацию, что и вся корреляционная матрица, а факторные нагрузки соответствуют коэффициентам корреляции. В нашем примере х₃ (потребности) имеет наибольшую фактор­ную нагрузку (1,12), а х, (способности) — наименьшую (0,36).

Глава 3. Статистический анализ экспериментальных данных

Следовательно, наиболее значимой причиной, влияющей на все остальные психологические переменные, в нашем случае явля­ются потребности, а наименее значимой — способности. Из кор­реляционной матрицы видно, что связи переменной х₃ со всеми остальными являются наиболее сильными (от 0,40 до 0,75), а кор­реляции переменной х₂ — самыми слабыми (от 0,16 до 0,40).

Чаще всего в итоге факторного анализа определяется не один, а несколько факторов, по-разному объясняющих матрицу интер­корреляций переменных. В таком случае факторы делят на ге­неральные, общие и единичные. Генеральными называются фак­торы, все факторные нагрузки которых значительно отличают­ся от нуля (нуль нагрузки свидетельствует о том, что данная пе­ременная никак не связана с остальными и не оказывает на них никакого влияния в жизни). Общие — это факторы, у которых часть факторных нагрузок отлична от нуля. Единичные — это факторы, в которых существенно отличается от нуля только одна из нагрузок. На рис. 75 схематически представлена структура факторного отображения переменных в факторах различной сте­пени общности.

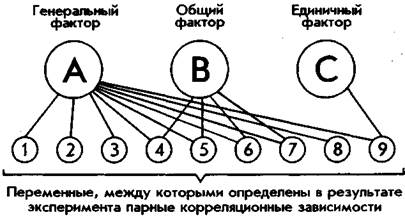
Рис. 75. Структура факторного отображения взаимосвязей переменных.

Отрезки, соединяющие факторы с переменными, указывают на высокие

факторные нагрузки

Часть II. Введение в научное психологическое исследование

Результаты психолого-педагогического эксперимента, или психологического тестирования, кроме их текстового описания, можно представить в виде таблиц, схем, графиков, рисунков и т.п. Таблицы представляют собой упорядоченные по горизонта­ли и по вертикали наборы количественных и качественных дан­ных, заключенных в рамки или без них. Таблицы могут иметь и не иметь названия, подзаголовки, указывающие на то, какие дан­ные в них содержатся.

Таблицы строятся и оформляются не произвольно, а в соот­ветствии с определенными правилами. Рассмотрим эти правила.

Таблицы, если их более двух-трех в тексте, нумеруются. Слово «таблица» обычно пишется справа или в середине вверху над таб­лицей. Непосредственно под ним располагается, если оно есть, название таблицы. Иногда для этого делаются примечания, ка­сающиеся некоторых особенностей материала, содержащегося в таблице. Такие примечания помещаются, как правило, непосред­ственно под таблицей. Таблица имеет заголовки, которые ука­зывают на то, что представлено в отдельных столбцах, а также рубрикацию по строкам, где обозначены особенности представ­ляемого материала.

Рассмотрим в качестве примеров формы и способы построе­ния типичных таблиц:

- не имеющей названия, без общего заголовка и примечаний (табл. 36);

- разграфленной, с названием и заголовком (табл. 37);

- разграфленной, с названием, заголовками и примечанием (табл. 38).

В таблице, построенной по образцу табл. 36, нет общего заго­ловка, который объединил бы названия всех столбцов, а есть толь­ко названия частных подзаголовков, относящиеся к отдельным столбцам. Нет также общего названия таблицы, так как содер­жание представленных в ней данных ясно само по себе. Имеют­ся названия отдельных строк таблицы — без них было бы непо­нятно, что характеризуют собой цифры, имеющиеся в строках

Глава 3. Статистический анализ экспериментальных данных

Таблица 36

	Начальные классы, I-V	Средние классы, VI—VIII	Старшие классы, IX-XI
Количество учащихся
Средний возраст (в годах)	10,5	12,5
Успеваемость (средняя оценка)	3,8	3,5	4,0
Уровень интеллектуального развития (IQ)	102%	104%	105%

таблицы. Подобного рода таблицы рекомендуется строить тог­да, когда общее количество данных, представляемых в столбцах и строках таблицы, относительно невелико (не более четырех раз­личных видов данных по столбцам и строкам, т.е. не более четы­рех столбцов и четырех строк). Во всех других случаях рекомен­дуется строить разграфленные таблицы с названиями, общими и частными подзаголовками (табл. 37).

Таблица 37 Результаты обследования шестилетних и семилетних детей с точки зрения их психологической готовности к обучению в школе (данные представлены в десятибалльной шкале оценок)

Возраст детей. Место их обучения и воспитания до поступления вшколу	Основные показатели психологической готовности детей к обучению в школе
интеллектуальные	личностные	межлич­ностные
вни­ма­ние	вооб­раже­ние	па­мять	мыш­ле­ние	речь	моти­вы уче­ния	ха­рак­тер	спо- соб- нос- ти	об-щи-тель-ность	кон­такт­ность
Шестилетние дети, посещавшие детский сад	7,2	7,6	7,9	8,0	7,1	6,2	7,2	8,0	8,4	8,4
Шестилетние дети, воспитанные дома	7,6	7,4	7,9	8,3	7,4	7,4	6,9	8,3	7,7	7,6
Семилетние дети, посещавшие детский сад	7,9	8,0	8,1	8,4	8,3	8,2	7,3	8,6	8,9	9,0
Семилетние дети, воспитанные дома	7,8	7,9	8,0	8,6	8,5	8,7	7,0	8,8	8,1	8,3

Часть II. Введение в научное психологическое исследование

В тех случаях, когда в таблице необходимо представить очень большое количество данных, которые невозможно полностью описать в подзаголовках столбцов или строк из-за громоздкости самих названий, обращаются к таблицам третьего типа (табл. 38), где соответствующие названия закодированы, а их расшифров­ка дается в примечании к таблице.

Таблица 38 Данные комплексного обследования детей из X классов средней школы

Услов­ные обозна­чения детей

Показатели обследования

I

II

III

А

Б

В

Примечание. А — Иванов, Б — Петров, В — Сидоров,...; I — социально-де­мографические данные о детях; II — успеваемость по отдельным предметам. III — данные о психологическом развитии; 1 — возраст, 2 — пол, 3 — социаль­ное происхождение, 4 — место жительства, 5 — математика, 6 — физика, 7 — история, 8 — география, 9 — внимание, 10 — память, 11 — мышление, 12 — речь.

Другой способ представления экспериментальных данных — графический. График на плоскости представляет собой некото­рую линию, которая изображает зависимость между двумя пе­ременными, а график в пространстве — плоскость, представляю­щую зависимость между тремя переменными. При использова­нии двумерного графика по горизонтальной линии на плоскос­ти обычно размещают независимую переменную — ту, которая из­меняется по намерению экспериментатора и рассматривается в качестве возможной искомой причины. По вертикали распола­гают зависимую переменную — ту, которая является или рассмат­ривается в качестве предполагаемой причины.

Глава 3. Статистический анализ экспериментальных данных

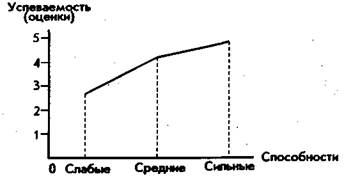
Рис. 76. График зависимости между способностями и успеваемостью учащихся¹.

Рис. 77. Трехмерное распределение экспериментальных данных. По оси X —

уровень эмоционального возбуждения, по оси У— уровень тревожности,

по оси Z — продуктивность деятельности.

Часть II. Введение в научное психологическое исследование

Если речь идет о трехмерном, пространственном графике, то по линиям X и Yb его горизонтальной плоскости чаще всего раз­мещают независимые, а по линии Z в вертикальной плоскости — зависимую переменную. Однако могут быть отступления от это­го правила. Они имеют место, например, тогда, когда в экспери­менте изучаются одна независимая и две зависимые переменные. В этом случае данные, касающиеся независимых переменных, размещаются вдоль вертикальной оси X, а данные, относящиеся к зависимым переменным, — вдоль осей Y и Z.

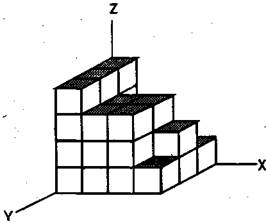
Рис. 79. Пример объёмной, или трёхмерной, гистограммы.

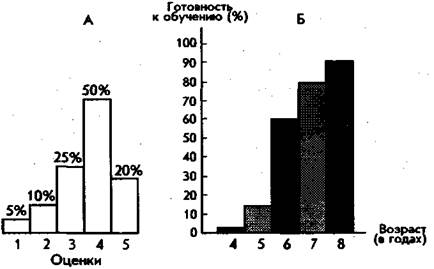
Рис. 78. Виды гистограмм «а плоскости. А — гистограмма распределения оценок в классе. Б — гистограмма распределе­ния показателей готовности де­тей разного возраста к обуче­нию в школе.

Глава 3. Статистический анализ экспериментальных данных

Рассмотрим два примера. На рис. 76 представлен плоско­стной, а на рис. 77 — пространственный графики.

Графики могут строиться по отдельным точкам (рис. 76) или представлять собой непрерывные линии (плоскости, рис. 77).

Особую разновидность графических изображений экспери­ментальных результатов представляют собой гистограммы. Это столбчатые диаграммы (рис. 78), состоящие из вертикальных прямоугольников, расположенных основаниями на одной пря­мой. Их высота отражает степень или уровень развитости того или иного качества у испытуемого. Цифры, указывающие на час­тоту встречаемости качества в выборке испытуемых, размеща­ются или внутри столбцов гистограммы, или над ними, или по вертикальной оси графика. Иногда для наглядности, особенно в том случае, если гистограмма соответствует трехмерному про­странству, ее изображают как объемную (рис. 79).

Контрольные вопросы

1. Для чего необходима математико-статистическая обработ­ка экспериментальных данных?

2. Классификация методов математической статистики и их назначение.

3. Как вычисляются среднее значение и дисперсия?

4. Каким образом определяются мода и медиана, какой цели они служат?

5. Для чего необходимо знать эмпирическое распределение экспериментальных данных?

6. Что такое интервал и с какой целью совокупность выбо­рочных данных разделяют на интервалы?

7. Методы вторичной статистической обработки экспери­ментальных данных.

8. Что такое критерий Стъюдента и в каких случаях он при­меняется?

9. Что такое критерий Фишера?

10. Что такое критерий х²?

11. Понятие о корреляции.

12. Коэффициент линейной корреляции.

13. Коэффициент ранговой корреляции.

14. Понятие о факторном анализе и его назначение.

Часть II. Введение в научное психологическое исследование

15. Общее представление о регрессионном исчислении.

16. Способы графического представления эксперименталь­ных данных.

17. Способы табличного представления экспериментальных данных.

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

1. Готтсданкер Р. Основы психологического эксперимента. М.:
МГУ, 1982. - 464 с.

(Корреляционные исследования: 378-424.)

2. ЗаксЛ. Статистическое оценивание. М., 1976.

(Что такое статистика: 37-39. Нормальная кривая и нормаль­ное распределение: 63-71. Арифметическое среднее и стандарт­ное отклонение: 72-79. Медиана и мода: 91-94. Распределение Стъюдента: 129-136. Хи-квадрат распределение: 136-150. Рас­пределение Фишера: 150-153. Сравнение двух выборочных дис­персий из нормальных совокупностей: 241-245. Сравнение двух выборочных средних из нормальных совокупностей: 245-270. Проверка распределений по хи-квадрат критерию согласия: 295-296. Коэффициент ранговой корреляции Спирмена: 368-372. Оце­нивание прямой регрессии: 371-381. Проверка равенства не­скольких дисперсий: 448-453).

3. Кулагин Б.В. Основы профессиональной психодиагностики. Л.,
1984.-216 с.

(Измерение в психодиагностике: 13-20. Корреляция и фактор­ный анализ: 20-33.)

4. Фресс П., Пиаже Ж. Экспериментальная психология. Вып. I и П.
М., 1966.

(Измерение в психологии: 197-229. Проблема надежности из­мерения: 229-231).

5. Практикум по общей психологии / Под ред. А.И. Щербакова.
М., 1990.-287 с.

[Методы психологии (с элементами математической статисти­ки): 20-39].

6. Психодиагностические методы (в комплексном лонгитюдном
исследовании студентов) / Под ред. А.А. Бодалева, М.Д. Дворя-
шиной, И.М. Палея. Л., 1976. - 248 с.

(Основные математические процедуры психодиагностического исследования: 35-51.)

________ Глава 4. Проведение экспериментального исследования _____

Глава 4.

ПОДГОТОВКА И ПРОВЕДЕНИЕ

ЭКСПЕРИМЕНТАЛЬНОГО

ПСИХОЛОГО-ПЕДАГОГИЧЕСКОГО

ИССЛЕДОВАНИЯ

Краткое содержание

Дата добавления: 2015-06-04