Водородоподобные атомы

Атомы, содержащие один внешний электрон называются водородоподобными. Потенциальная энергия электрона в таких атомах определяется сферически симметричным полем взаимодействия его с ядром (рис. 1.9):

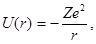(1.54)

где Z - зарядовое число атома, r - расстояние электрона от ядра.

Для электрона, связанного с атомом, E < 0, а для свободно движущегося вне атома соответствует положительная полная энергия (E > 0).

Уравнение Шредингера для электрона в атоме имеет вид

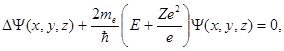(1.55)

где m_e - масса электрона.

В сферической системе координат уравнение (1.55) преобразуется к виду

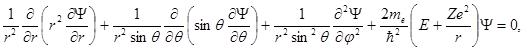(1.56)

где 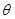и 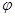- полярный и азимутальный углы соответственно.

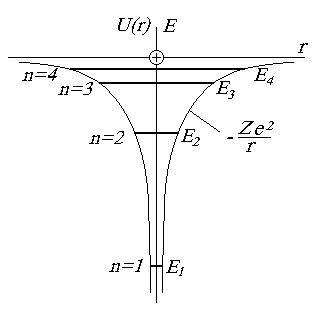
Рис. 1.9. Энергетическая диаграмма водородоподобного атома

Для E < 0 уравнение (1.56) имеет конечные и непрерывные решения только для дискретных значений энергии

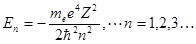, (1.57)

Собственные функции, удовлетворяющие уравнению (1.56), зависят от трех целочисленных параметров n, l и m:

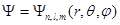
Параметр n называется главным квантовым числом и определяет полную энергию электрона в атоме (см. формулу (1.57)). Этим числом обозначают номер энергетического уровня электрона в атоме (рис. 1.9).

Параметр l определяет модуль момента импульса электрона в атоме:

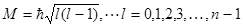
и называется азимутальным или орбитальным квантовым числом. При данном главном квантовом числе n квантовое число l может принимать n различных значений от 0 до n-1.

Параметр m определяет величину проекции момента импульса на некоторое направление z

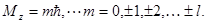
Этот параметр называется магнитным квантовым числом.

Таким образом, каждому значению энергии электрона в атоме соответствует несколько состояний, отличающихся квантовыми числами l и m, и собственными волновыми функциями 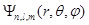. Такие состояния называются вырожденными. Кратность вырождения, т.е. число различных состояний с данным значением энергии, как нетрудно убедиться, будет равно .

Волновая функция 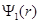состояния с наинизшей энергией (n = 1) в сферически симметричном случае имеет вид

, (1.58)

где . Физический смысл этого параметра будет понятен из дальнейшего анализа.

Функция определяет, как обычно, объемную плотность вероятности обнаружения электрона в пространстве. Более наглядное представление можно получить с помощью радиальной плотности вероятности . Эта величина вводится таким образом, чтобы произведение 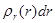определяло вероятность обнаружения электрона на расстоянии от ядра между r и r+dr. Расчеты приводят к следующему выражению для :

.

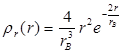На рис. 1.10 представлен график функции . Он имеет максимум при r=r_B. Для атома водорода численное значение r_B совпадает с радиусом первой боровской орбиты. Следовательно, в квантовой физике радиус первой боровской орбиты соответствует такому расстоянию от ядра, на котором вероятность обнаружения электрона максимальна.

Для полного описания состояния электрона в атоме необходимо к трем квантовым числам n, l, m добавить еще одно - спиновое квантовое число (спин) S. Это квантовое число определяет ориентацию собственного момента количества движения электрона на некоторое направление, например, на направление орбитального момента электрона. Квантовое число S может принимать только два значения: и 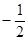. Наличие спина приводит к удвоению состояний электрона в атоме. Спин не имеет классического аналога, это такое же внутреннее свойство электрона, как его заряд и масса.

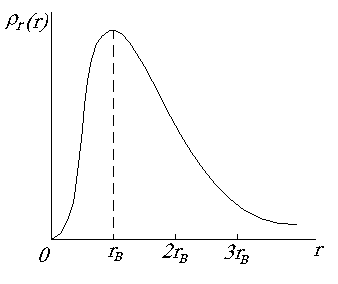
Рис. 1.10. График функции для состояния электрона в атоме водорода с n = 1

ГЛАВА 2

Дата добавления: 2015-06-04