
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уровень Ферми в полупроводниках
|
|
|
|
Понятия энергии Ферми и уровня Ферми были введены ранее для металлов. Поскольку в полупроводниках функция распределения электронов по состояниям имеет тот же вид, что и в металлах, то энергия Ферми в полупроводниках имеет тот же физический смысл: энергия Ферми - это максимально допустимая энергия, ниже которой при нулевой абсолютной температуре все энергетические уровни заняты [ f(E) = 1], а выше которой все уровни пусты [ f(E) = 0]. Для полупроводников, у которых при абсолютном нуле валентная зона полностью заполнена, а зона проводимости совершенно свободна, функция распределения имеет разрыв. Следовательно, уровень Ферми в полупроводнике должен лежать при абсолютном нуле в запрещенной зоне.
Для собственного полупроводника концентрации электронов и дырок равны (n = p), т.к. каждый электрон, покинувший валентную зону, создает одну дырку. Приравнивая равенства (3.17) и (3.19), получим
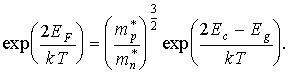
Разрешая последнее равенство относительно ЕF, получим
 (3.23)
(3.23)
Если эффективные массы электронов и дырок равны [ 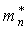 =
= 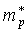 ,
,  = 0] уровень Ферми собственного полупроводника при любой температуре располагается посередине запрещенной зоны.
= 0] уровень Ферми собственного полупроводника при любой температуре располагается посередине запрещенной зоны.
Температурная зависимость положения уровня Ферми в собственном полупроводнике определяется третьим слагаемым в уравнении (3.23). Если эффективная масса дырки в валентной зоне больше эффективной массы электрона в зоне проводимости, то уровень Ферми смещается с повышением температуры ближе к дну зоны проводимости. В противоположном случае уровень Ферми смещается к потолку валентной зоны. Положение уровня Ферми в собственном полупроводнике с изменением температуры схематически показано на рис. 3.5.
Для большинства полупроводников эффективная масса дырки не намного превышает эффективную массу электрона и смещение уровня Ферми с изменением температуры незначительно. Однако у антимонида индия (InSb) 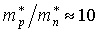 , а ширина запрещенной зоны невелика (Eg = 0,17 эВ), так что при Т > 450 K уровень Ферми входит в зону проводимости. При этой температуре полупроводник переходит в вырожденное состояние.
, а ширина запрещенной зоны невелика (Eg = 0,17 эВ), так что при Т > 450 K уровень Ферми входит в зону проводимости. При этой температуре полупроводник переходит в вырожденное состояние.
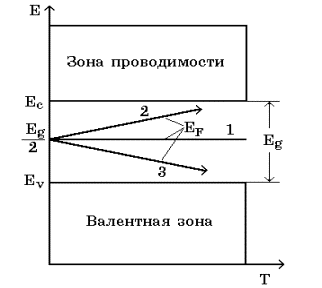 Рис. 3.5. Положение уровня Ферми в собственном полупроводнике
1 -
Рис. 3.5. Положение уровня Ферми в собственном полупроводнике
1 - 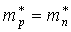 ; 2 - ; 2 - 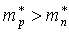 ; 3 - ; 3 - 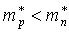 . .
|
Положение уровня Ферми в примесных полупроводниках может быть найдено из условия электронейтральности кристалла. Для донорного полупроводника это условие записывается в виде
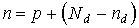 , (3.24)
, (3.24)
здесь Nd - концентрация донорных уровней, nd - концентрация электронов на донорных уровнях. Концентрация электронов в зоне проводимости равна сумме концентраций дырок в валентной зоне и концентрации положительно заряженных ионов доноров (последняя, очевидно, равна Nd - nd).
Концентрацию электронов на донорных уровнях можно вычислить, умножив концентрацию этих уровней Nd на функцию распределения Ферми-Дирака:
 , (3.25)
, (3.25)
где Еd - энергия активации донорных уровней.
Подстановка в условие электронейтральности (3.24) концентраций электронов (3.17) и дырок (3.19), а также концентрации электронов на донорных уровнях (3.25) приводит к следующему уравнению относительно положения уровня Ферми ЕF:
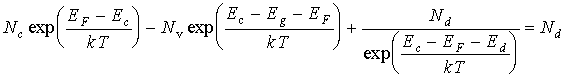 . (3.26)
. (3.26)
При подстановке концентрации электронов на донорных уровнях в уравнение (3.24) было сделано предположение, что газ электронов примесных атомов невырожденный, что позволило пренебречь единицей в знаменателе формулы (3.25).
Уравнение (3.26) ввиду его сложности обычно в общем виде не решают, а ограничиваются рассмотрением частных случаев. Например, при низких температурах, когда электроны в зоне проводимости появляются в основном за счет переходов с примесных уровней, а концентрация дырок близка к нулю, решение уравнения (3.26) имеет вид
 . (3.27)
. (3.27)
Из уравнения (3.27) следует, что при абсолютном нуле температуры энергия Ферми донорного полупроводника находится строго посередине между дном зоны проводимости и донорными уровнями. Температурная зависимость положения уровня Ферми определяется третьим членом в уравнении (3.27), который меняет знак с изменением температуры. Поэтому уровень Ферми с повышением температуры сначала смещается к зоне проводимости, а затем - к валентной зоне (рис. 3.6,а).

Аналогично можно получить выражение для температурной зависимости уровня Ферми в акцепторном полупроводнике. График этой зависимости схематически приведен на рис. 3.6,б.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 3364; Нарушение авторских прав?; Мы поможем в написании вашей работы!