Энергия Ферми. Влияние температуры на распределение Ферми-Дирака

Функция распределения Ферми-Дирака. Уровень Ферми.

Функция распределения Ферми-Дирака, описывающая распределение фермионов по состояниям, имеет следующий вид:

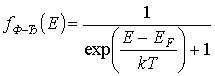, (3.4)

здесь E_F - химический потенциал системы фермионов, т.е. работа, которую необходимо затратить, чтобы изменить число частиц в системе на одну. В случае электронов величина E_F называется энергией Ферми.

Рассмотрим вид функции Ферми-Дирака при температуре, стремящейся к абсолютному нулю. Как нетрудно видеть из формулы (3.4), для любой энергии частицы, большей энергии Ферми, экспонента в знаменателе стремится к бесконечности при 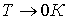, следовательно f(Е) стремится к нулю. Это значит, что все энергетические состояния с Е > E_F совершенно свободны при абсолютном нуле. Если Е < E_F при 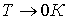, f(E) стремится к единице. Это значит, что все квантовые состояния с энергией, меньше энергии Ферми, полностью заняты электронами. Отсюда понятен физический смысл энергии Ферми как параметра распределения электронов по состояниям: энергия Ферми есть максимально возможная энергия электронов в металле при температуре абсолютного нуля. Энергетический уровень, соответствующий энергии Ферми, называется уровнем Ферми.

Вид функции распределения Ферми-Дирака при Т = 0К представлен на рис. 3.2,а. На рис. 3.2,б показано распределение электронов по энергетическим уровням в зоне проводимости металла при этой же температуре.

Если Т  0К, то при энергии частицы, равной энергии Ферми, функция распределения Ферми-Дирака равна 1/2. Это значит, что при любой температуре, отличающейся от абсолютного нуля, уровень Ферми заполнен наполовину. Вид функции Ферми-Дирака для двух различных температур показан схематически на рис. 3.3. Изменение характера распределения электронов по состояниям связано с тепловым возбуждением электронов. При этом часть электронов переходит в состояния с энергиями, большей энергии Ферми. Соответственно часть состояний ниже уровня Ферми оказывается свободной. В результате функция f(E) "размыта" вблизи энергии Ферми. Тепловому возбуждению подвергается незначительная часть электронов, находящихся вблизи уровня Ферми. Функция Ферми-Дирака заметно отличается от вида, который она имела при абсолютном нуле, лишь при 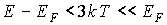. Величина "размытия" пропорциональна температуре (рис. 3.3). Чем выше температура, тем более существенному изменению подвергается функция распределения.

Рис. 3.3. Функция распределения Ферми-Дирака при Т>0K

Рис. 3.2. Функция распределения Ферми-Дирака (а) и распределение электронов в зоне проводимости металла при Т=0К (б)

При условии

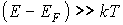(3.5)

экспонента в знаменателе становится значительно больше единицы в формуле (3.4). В этом случае единицей можно пренебречь и распределение Ферми-Дирака преобразуется к виду

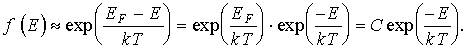(3.6)

Выражение (3.6) совпадает по форме с функцией распределения Максвелла-Больцмана.

Вероятность того, что некоторый энергетический уровень с энергией Е свободен, т.е. занят дыркой, равна

(3.7)

Таким образом, функция распределения Ферми-Дирака для дырок аналогична функции распределения для электронов, если в ней изменить знаки показателей экспонент. Это хорошо согласуется с представлением о том, что дырки являются носителями положительного заряда.

Газ носителей заряда, подчиняющийся статистике Ферми-Дирака, называется вырожденным. Если носители заряда подчиняются статистике Максвелла-Больцмана, то они называются невырожденными.

Дата добавления: 2015-06-04