Титрования

Фотометрическое титрование без индикатора. Вид кривых

Фотометрическое титрование без индикатора возможно, если в точке эквивалентности происходит резкое изменение светопоглощения титруемого раствора.

В зависимости от соотношения величин молярных коэффициентов светопоглощения растворов титруемого вещества, титранта и продукта их взаимодействия и изменения концентраций всех веществ системы при титровании, кривые фотометрического титрования могут иметь разный вид.

Предположим, при титровании протекает реакция:

А + В АВ,

где А – титруемое вещество;

В – титрант;

АВ – продукт реакции.

Концентрация веществ в титруемой системе изменяются так:

до точки эквивалентности [A] – уменьшается,

[B] = 0, не возрастает

[AB] – увеличивается,

после точки эквивалентности [A] = 0, не возрастает

[B] – увеличивается,

[AB] = const, не возрастает

Следует, что изменение оптической плотности титруемой системы до точки эквивалентности определяется разностью

∆А = А(АВ) – А(А), (4)

а после точки эквивалентности –

∆А = А(В) – А(АВ) (5)

В точке эквивалентности оптическая плотность титруемой системы равна А(АВ). В выражениях (4) и (5)

А(А) – оптическая плотность титруемого раствора;

А(В) – оптическая плотность титранта;

А(АВ) – оптическая плотность продукта реакции.

Пользуясь уравнениями (4) и (5), а также основным законом светопоглощения, ход кривых титрования до и после точки эквивалентности, можно предположить и объяснить:

если ∆А > 0, на кривой – подъём;

если ∆А = 0, на кривой – горизонталь;

если ∆А < 0, на кривой – спад.

На рисунке 8 приведены некоторые возможные виды кривых спектрофотометрического титрования для случаев:

Кривая 1 ε (АВ) > 0 (вещество окрашено при заданной λ)

ε (В) = 0 (вещество бесцветно)

ε (АВ) = 0

Кривая 2 ε (А) = 0 Кривая 3 ε (А) = 0

ε (В) = 0 ε (В) > 0

ε (АВ)>0 ε (АВ) = 0

Кривая 4 ε (А) > 0

ε (В) > 0

ε (АВ) = 0

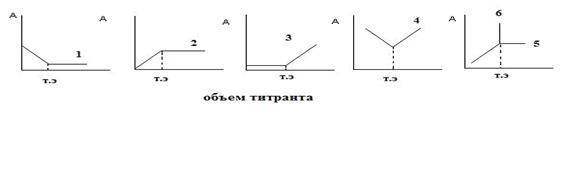
Рисунок 8 – Кривые спектрофотометрического титрования

Кривая 5 ε (А) = 0 Кривая 6 ε (А) = 0

ε (В) > 0 ε (В) > 0

ε (АВ) > 0 ε (АВ) > 0

ε (АВ) > ε (В) ε (АВ) < ε(В)

Возможен ещё один случай: поглощают свет при заданной длине волны, т.е. окрашены все компоненты (ε(А) > 0; ε(В) > 0; ε(АВ) > 0). Вид кривых в этом случае показан на рисунке 9:

V, мл

Рисунок 9

Кривая 7: ε(А) < ε(АВ)

Кривая 8: ε(А) = ε(АВ)

Кривая 9: ε(А) > ε(АВ)

Возможно проводить спектрофотометрическое титрование нескольких веществ при совместном присутствии в растворе. При этом на кривой титровании будет несколько точек эквивалентности. Но условия титрования требуют особого рассмотрения (порядок взаимодействия компонентов титруемой смеси с титрантом, одинаковые или разные длины волн света требуются для определения каждого компонента, мешающее действие всех веществ титруемой системы друг на друга и т.п.).

Дата добавления: 2015-06-04