
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аксиомы стат
|
|
|
|
1. Аксиома о равновесии сист. двух сил. Твердое тело под действием двух сил находится в равновесии тогда и только тогда, когда силы равны по модулю и направлены в противоположные стороны по общей линии действия.
2. Аксиома 2. Состояние тела не изменится если к действующей на него системе сил прибавить или отнять от нее уравновешенную систему сил.
Следствие из аксиом 1,2. Силу, действующую на твердое тело, можно не изменяя состояния тела переносить параллельно себе вдоль линии действия силы в любую точку тела.
3. Аксиома 3 (аксиома параллелограмма). Две силы, приложенные к твердому телу в одной точке, имеют равнодействующую, приложенную в этой же точке и являющейся диагональю параллелограмма, построенного на векторах сил как на сторонах.
4. Аксиома 4 (аксиома равенства действия и противодействия). Силы взаимодействия двух тел всегда равны по модулю и противоположно направлены по одной прямой.
Тело называется свободным, если его перемещение в пространстве не ограничено другими телами, в противном случае тело называется несвободным.
Связи - тела, ограничивающие перемещение данного тела.
Аксиома 6 (аксиома освобождаемости от связей). Любое несвободное тело можно считать свободным, если связи его мысленно отбросить и заменить их действие реакциями связей.
1. Гладкая опорная поверхность. Если твердое тело опирается на идеально гладкую (без трения) поверхность, то реакция поверхности R направлена по нормали к ней в точке соприкосновения, т. е. перпендикулярно к касательной плоскости в данной точке поверхности. Такая реакция называется нормальной реакцией.
2. Гибкая нить.
T – сила натяжения нити, которая направлена вдоль нити и всегда от тела, равновесие которого будет рассматриваться.
3. Прямолинейный стержень, закрепленный шарнирно.
4. Цилиндрический шарник (подшипник). Цилиндрическим шарниром называется совокупность неподвижного валика и надетой на него втулки, соединенной с твердым телом При этом твердое тело может поворачиваться вокруг оси валика. Направление реакции неподвижного цилиндрического шарнира A сразу указать нельзя, поэтому при решении задач реакция шарнира заменяется двумя взаимно перпендикулярными составляющими XA и YA. Определив в ходе решения задачи XA и Y A можно найти модуль и направление реакции шарнира. Реакцию шарнира можно разложить на составляющие по любым двум направлениям.
Если цилиндрический шарнир подвижный то он не противодействует перемещению вдоль прямой, по которой могут катиться колеса, поэтому возникает только одна составляющая RB, перпендикулярная плоскости качения.
5. Сферический шарнир (подпятник). В случае сферического шарнира
(рис. 8) также нельзя заранее указать направление реакции шарнира При решении задач реакция сферического шарнира заменяется тремя взаимно перпендикулярными составляющими XA, YA, Z
6.Жесткая заделка. Балка АВ не может в месте закрепления А ни перемещаться ни вращаться, поэтому реакции такого типа связи имеют составляющие XA, YA ,MA, где МА – это момент пары сил, противодействующий вращению балки вокруг точки А.
Порядок решения задач статики на равновесие твердого тела.
Выбирается объект равновесия (некоторое твердое тело).
1. Показываются активные силы, приложенные к объекту равновесия.
2. Применяется аксиома освобождаемости от связей: связи мысленно отбрасываются, а их действие заменяется реакциями связей, приложенными к объекту равновесия.
3. Определяется вид системы сил, действующей на объект равновесия, и составляются соответствующие уравнения (условия) равновесия.
4. Решая уравнения, определяются неизвестные величины.
Сходящаяся система сил
Система сил называется сходящейся, если линии действия сил пересекаются в одной точке. Сходящуюся систему сил можно заменить равнодействующей геометрическим или векторным способом или аналитически по формулам (1)- (4).
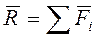 , (
, ( 1)
1)
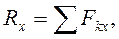
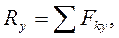
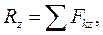 (2)
(2)
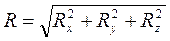 , (3)
, (3)
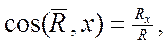
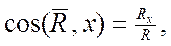
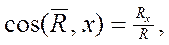 (4)
(4)
Условия равновесия сходящейся системы сил.
Для равновесия сходящейся системы сил необходимо и достаточно, чтобы выполнялись условия:
1. геометрическое или векторное условие: силовой многоугольник, построенный на векторах сил как на сторонах должен быть замкнут
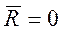 , или
, или 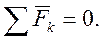 (5)
(5)
2. Аналитические уравнения равновесия:
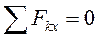 ,
, 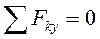 ,
, 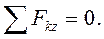 (6)
(6)
Если все силы сходящейся системы лежат в одной плоскости то следует выбрать систему координат в этой плоскости и использовать только два уравнения.
Теорема о трех силах – если тв. тело под действием трех сил, две из которых пересекаются в одной точке, находится в равновесии, то лини действия таких трех сил пересекаются в одной в одной точке.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 475; Нарушение авторских прав?; Мы поможем в написании вашей работы!