Произвольная плоская система сил

Если плоская система сил не является сходящейся, то для вывода условий равновесия нужно заменить систему сил на более простую. Это называется приведением системы сил.

Момент силы относительно точки на плоскости (алгебраический) –это взятое со знаком плюс или минус произведение модуля силы на плечо силы относительно точки. Плечо силы относительно точки – это кратчайшее расстояние от точки до линии действия силы, т е длина перпендикуляра, опущенного из точки на линию действия силы

Теоремы о свойствах пар в плоскости.

1. Момент пары сил равен алгебраической сумме моментов сил образующих пару, вычисленных относительно произвольной точки на плоскости.

2. Две пары сил, лежащие в одной плоскости, эквивалентны тогда и только тогда, когда равны их алгебраические моменты.

3. Система пар сил, лежащих в одной плоскости, эквивалентна одной паре, момент которой равен алгебраической сумме моментов этих пар.

4. Система пар сил, лежащих в одной плоскости, уравновешивается тогда и только тогда, когда алгебраическая сумма моментов этих пар равна нулю.

Условия равновесия произвольной плоской системы сил.
Для равновесия произвольной плоской системы сил необходимо и достаточно чтобы главный вектор R’ и главный момент m_O относительно произвольно выбранного центра приведения равнялись нулю,

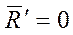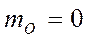, , (10)

или в аналитической форме

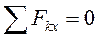
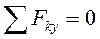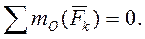, (11)

Оси x, y системы координат и точку в уравнении моментов можно выбирать произвольно.

Теорема Вариньона для произвольной плоской системы сил. Если система сил приводится к равнодействующей, то момент равнодействующей относительно произвольной точки равен сумме моментов слагаемых сил относительно той же точки

Приведение силы к заданному центру: силу можно переносить параллельно самой себе в любую точку тв. тела, добавляя при этом пару сил, векторный момент которой равен векторному моменту переносимой силы относительно новой точки приложения силы

Приведение произвольной сист. сил к силе и паре сил: (теор. Пуансо) любую произвольную сист. сил, действующих на тв. тело, можно в общем случае привести к силе и паре сил (Приведение сист. сил к заданному центру)

Основная теорема статики: любую сист. сил, действующ. на тв. тело, можно привести к силе, равной главному вектору сист. сил, и паре сил, векторный момент которой равен главному моменту сист. сил относительно точки, выбранной за центр приведения.

Частные случаи приведения плоской системы сил

1 случай приведения к равнодействующей силе: если при приведении плоской сист. сил к какому либо центру окажется, что вектор

R 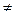0, а главный момент L=0, то такая плоская система сил приводится к одной силе R*-равнодействующей системы сил.

если при приведении плоской сист. сил главн. вектор не равен 0 и главн. мом. не равен 0, то такую сист. можно привести к одной равнодействующей силе R*

2 случай приведения к паре сил: если при превидении плоской сист. сил к какому либо центру окажется, что главный вектор R=0, а главн мом L 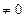,то такую плоскую систему можно привести к одной паре сил, алгебраический момент которой равен главному мом системы сил относительно центра пиведения, и в этом случае главный момент не зависит от выбора центра приведения.

Теорема Вариньона о моменте равнодействующей: векторный момент равнодействующей рассматриваемой системы сил относительно любой точки равен сумме векторных моментов всех сил этой системы относительно той же точки.

(для плоской системы сил) алгебраический момент равнодействующей плоской сист. сил относительно любой точки, лежащей в плоскости действия сил, равен сумме алгебраических моментов всех сил этой системы относит. той же точки.

Дата добавления: 2015-06-04