Плоскости частного положения

Способы задания плоскости

Плоскость считается заданной; если из всех точек пространства можно выделить только те точки, которые принадлежат данной плоскости. Плоскость на чертеже может быть определена следующими способами (каждый из способов допускает переход к любому другому способу).

1. Тремя точками, не лежащими на одной прямой (рис. 4.1а).

2. Прямой и точкой вне прямой (рис. 4.1б).

3. Двумя пересекающимися прямыми (рис. 4.1в).

4. Двумя параллельными прямыми (рис. 4.1г).

5. Любой плоской фигурой-отсеком пространства (рис. 4.1д).

Рис. 4.1а. Три точки.

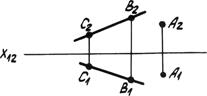
Рис. 4.1б. Прямая и точка.

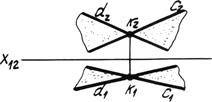
Рис. 4.1в. Пересекающиеся прямые.

Рис. 4.1г. Параллельные прямые.

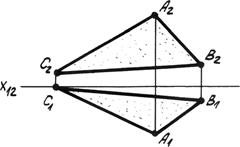
Рис. 4.1д. Фигура.

6. Следами плоскости (рис. 4.2).

Следы плоскости - это линии пересечения плоскости с плоскостями проекций.

Линия пересечения плоскости с плоскостью p₁ называется горизонтальным следом плоскости Q ₁, с плоскостью p₂-фронтальным следом Q ₂, с плоскостью p₃-профильным следом Q ₃. Точки пересечения следов на осях проекций называются точками схода следов Q _x, Q _y, Q _z.

Отрезки OQ _x, OQ _y, OQ _z, отсекаемые осями проекций, называют параметрами плоскости (рис. 4.2).

Рис. 4.2. Следы плоскости.

Плоскости относительно плоскостей проекций могут быть общего и частного положения. Плоскости частного положения - это плоскости перпендикулярные или параллельные какой-либо плоскости проекций.

Плоскости перпендикулярные одной из плоскостей проекций, называются проецирующими.

1. Горизонтально проецирующая плоскость перпендикулярна горизонтальной плоскости проекций p₁ (рис. 4.3а).

Рис. 4.3а. Горизонтально проецирующая плоскость.

Фронтальный след S₁ перпендикулярен оси x. Профильный след S₃ перпендикулярен оси y.

Ða - угол наклона плоскости S к плоскости p₂. Ðb - угол наклона плоскости S к плоскости p₃. Горизонтальная проекция всех точек плоскости S совпадает с её горизонтальными следами.

2. Фронтально проецирующая плоскость перпендикулярна фронтальной плоскости проекций p₂ (рис. 4.3б) горизонтальный след l₁ - перпендикулярен оси x, профильный след l₃ перпендикулярен оси z, Ðj - угол наклона плоскости l к плоскости p₁. Ðb - угол наклона плоскости l к плоскости p₃. Фронтальные проекция всех точек плоскости l совпадают с ее фронтальным следом.

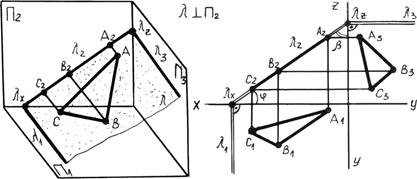
Рис. 4.3б. Фронтально проецирующая плоскость.

3. Профильно проецирующая плоскость перпендикулярна профильной плоскости проекций p₃ (рис. 4.3.в).

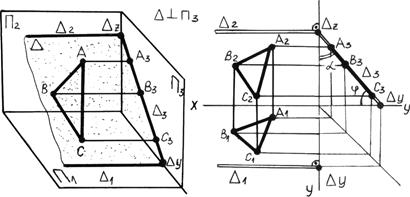
Рис. 4.3в. Профильно проецирующая плоскость.

Горизонтальный след D₁ перпендикулярен оси y, фронтальный след D₂ перпендикулярен оси z.

Ðj - угол наклона плоскости D к плоскости p₁.Ða - угол наклона плоскости D к плоскости p₂. Профильные проекции всех точек плоскости D совпадают с ее профильным следом.

Плоскости параллельные какой-либо из плоскостей проекций и перпендикулярные двум другим называются плоскостями уровня.

1. Горизонтальные плоскость уровня параллельна плоскости p₁ и перпендикулярна плоскостям p₂ и p₃ (рис. 4.4а).

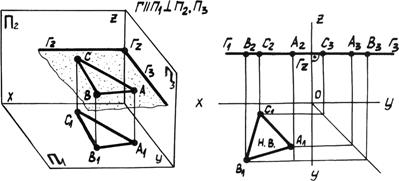
Рис. 4.4а. Горизонтальные плоскость уровня.

Фронтальная и профильная проекции плоскости совпадают с ее следами G₁ и G₂, которые перпендикулярны оси z. На горизонтальную плоскость p₁ любая фигура, расположенная в плоскости G, проецируется без искажения на p₁.

2. Фронтальная плоскость уровня параллельна плоскости p₂ и перпендикулярна плоскостям p₁ и p₃ (рис. 4.4б).

Горизонтальная и профильная проекции плоскости совпадают с её следами q₁ и q₃, которые перпендикулярны оси y. На фронтальную плоскость p₂ любая фигура, расположенная в плоскости q, проецируется без искажения.

Рис. 4.4б. Фронтальная плоскость уровня.

3. Профильная плоскость уровня параллельна плоскости p₃ и перпендикулярна плоскостям p₂ и p₃ (рис. 4.4в).

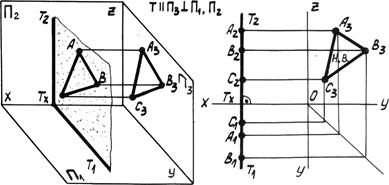
Рис. 4.4в. Профильная плоскость уровня.

Фронтальная и горизонтальная проекции плоскости совпадают с её следами Т₁ и Т₂, которые перпендикулярны оси x. На профильную плоскость p₃ любая фигура, расположенная в плоскости Т, проецируется без искажения.

Свойства плоскостей частного положения:

1. Любая геометрическая фигура расположенная в плоскости, перпендикулярной какой-либо плоскости проекций, проецируется на соответствующий след этой плоскости.

2. Любая геометрическая фигура расположенная в плоскости уровня, проецируется без искажения на ту плоскость проекций, которой данная плоскость параллельна.

Дата добавления: 2015-06-29