Пересекающиеся плоскости

Прямая линия, параллельная плоскости.

Прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в плоскости (рис. 4.12).

Через каждую точку пространства можно провести бесконечное множество прямых, параллельных данной плоскости Р.

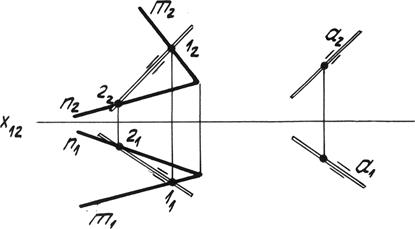
Рис. 4.12. Прямая линия параллельная плоскости.

Задача: Через точку С провести прямую а параллельную плоскости Р (рис. 4.13).

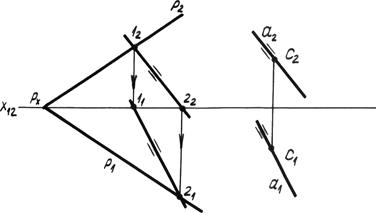
Рис. 4.13.

Решение: Одну из проекций искомой прямой а ₂ проведём произвольно через точку С ₂. Определим в данной плоскости P прямую параллельную прямой а. Горизонтальная проекция прямой а ₁ будет параллельна горизонтальной проекции прямой в плоскости а ₂ || (1₂2₂) и а ₁ || (1₁2₁).

Две плоскости пересекаются по прямой линии, для построения которой достаточно, или определить две общие для плоскостей точки, или одну точку и направление линии пересечения.

Рассмотрим задачи на построение проекций линии пересечения плоскостей и их положения относительно плоскостей проекций.

1. Если плоскости заданы следами и следы пересекаются в пределах чертежа (рис. 4.14а) то, две точки линии пересечения определяются на пересечение одноимённых следов. Точка 1 – пересечение горизонтальных следов, точка 2 – пересечение фронтальных следов. Линия l (1₁1₂) - линия пересечения плоскостей l и å.

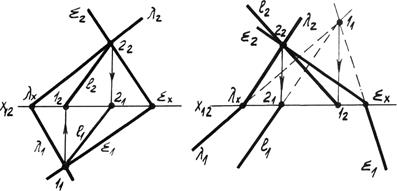
Рис. 4.14а. Плоскости заданы следами.

2. Один из частных случаев пересечения плоскостей, когда одна из них является проецирующей плоскостью (рис. 4.14б).

Задача сводиться к определению второй проекции линии, принадлежащей и проецирующей плоскости, и плоскости общего положения.

Определяем точки пересечения соответствующего следа проецирующей плоскости с плоскостью общего положения точки 1 и 2. По линиям связи определяем вторую проекцию. Затем необходимо определить видимость отсеков плоскости общего положения относительно линии пересечения.

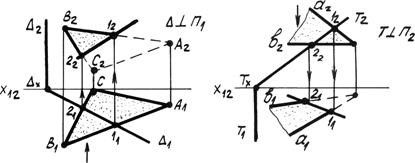
Рис. 4.14б. Одна из плоскостей проецирующая.

3. В некоторых случаях линия пересечения плоскостей является линией частного положения (рис. 4.14в).

Рассмотрим задачи на пересечение плоскостей по горизонтали. В первой задаче одна из плоскостей l является горизонтальной плоскостью уровня, поэтому фронтальная линия проекции пересечения h ₂ совпадает со следом этой плоскости и является горизонталью. Горизонтальная проекция определяется по точке 1 пересечения следов и направлению h ₁ || l₁.

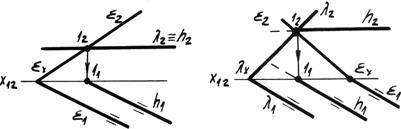
Рис. 4.14в. Пересечение по линиям частного положения.

Во второй задаче горизонтальные следы плоскостей общего положения параллельны l₁ || å₁. Следовательно, горизонтальная проекция линии пересечения будет им параллельна h ₁ || l₁ || å₁, а фронтальная будет проходить через точку 1 пересечения фронтальных следов.

Аналогичны случаи пересечения по фронтали. Существуют другие частные случаи пересечения плоскостей, когда линией пересечения являются проецирующие прямые.

4. Общий случай пересечение плоскостей, когда в пределах чертежа сразу не определяются общие для данных плоскостей точки. Для решения такой задачи используются вспомогательные секущие плоскости обычно частного положения – или плоскости уровня, или проецирующие.

Рассмотрим пример на рис. 4.15.

Даны две плоскости, заданные параллельными прямыми (а || b) и треугольником АВС. Для определения двух общих точек данных плоскостей решаем задачу по алгоритму:

1. Вводим первую вспомогательную горизонтальную плоскость уровня å.

2. Строим линии пересечения каждой данной плоскости со вспомогательной (а || b) Ç å ® h ^å (ABC) Ç å ® h ^å. Эти линии являются горизонталями данных плоскостей.

3. Определяем точку пересечения линии пересечения. Точка I – общая для данных плоскостей.

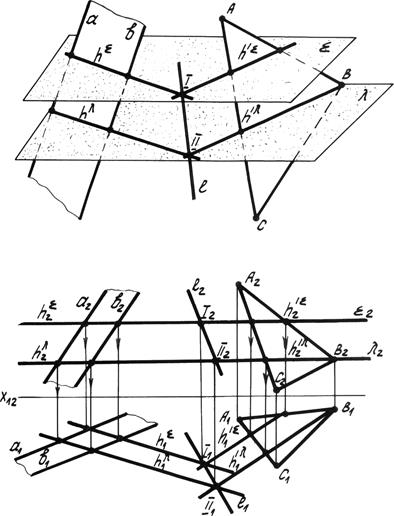
Рис. 4.15. Общий случай пересечения плоскостей.

4. Для определения ещё одной общей точки выводим вторую вспомогательную секущую плоскость уровня. l Выполним те же построения и определим вторую общую точку II.

5. Соединяем получившиеся точки I и II, Которые определяют линии пересечения плоскостей l (l ₁, l ₂).

При решении некоторых задач удобнее использовать вспомогательные проецирующие плоскости.

Дата добавления: 2015-06-29