Взаимно перпендикулярные плоскости

Прямая линия, перпендикулярная плоскости.

Прямая линия перпендикулярна плоскости, если она перпендикулярна любым двум пересекающимся прямым плоскости.

Однако распознать перпендикулярность прямой линии и плоскости в общем случае сложно, т.к. прямой угол проецируется на плоскость проекции в натуральную величину, когда одна из его сторон параллельна данной плоскости проекций. Следовательно, если на некоторой плоскости å (рис. 4.19) провести две пересекающиеся прямые, одна из которых горизонталь h || p, а другая - фронталь f || p₂, то перпендикулярная к плоскости å прямая a проецируется на плоскость p₁ перпендикулярно h ₁, а плоскость p₂ перпендикулярна f ₂.

Рис. 4.19. Прямая линия, перпендикулярная плоскости.

Итак: если прямая линия перпендикулярна к плоскости, то её горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали, а её фронтальная проекция – перпендикулярна фронтальной проекции фронтали, а также к одноимённым следам.

На рис. 4.19 рассмотрены случаи построения перпендикуляра из точки K к треугольнику АВС и к плоскости å, заданной следами. Если плоскости заданы не следами, то первоначально всегда требуется определить горизонталь и фронталь в плоскости.

Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Для построения плоскости перпендикулярной к данной достаточно определить прямую линию ей перпендикулярную. Через перпендикуляр к плоскости можно провести множество плоскостей, перпендикулярных данной (рис. 4.20а).

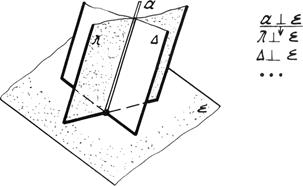
Рис. 4.20а. Взаимно перпендикулярные плоскости.

Рассмотрим построение одной из плоскостей, перпендикулярной данной плоскости (c Ç d) (рис. 4.20б).

рис. 4.20б. Взаимно перпендикулярные плоскости.

Определим горизонталь h и фронталь ¦ данной плоскости. Из произвольной точки K восставим перпендикуляр a на горизонтальной проекции a ₁ ^ h ₁, а на фронтальной проекции a ₂ ^ ¦₂. Дополним прямую a до плоскости пересекающейся с ней произвольной прямой b. Плоскость (a Ç b) перпендикулярна плоскости (c Ç d).

Вопросы и задачи для самоконтроля

1. Какими способами можно задать плоскость на чертеже?

2. Как можно перейти от любого способа задания плоскости к способу задания следами?

3. При каких условиях точка и прямая принадлежат плоскости?

4. Какие прямые линии в плоскости называются главными, и как они направлены?

5. Сформулируйте условия параллельности прямой линии плоскости и условия параллельности плоскостей.

6. Когда прямой угол между прямой линией и плоскостью проецируется в натуральную величину?

7. В каких случаях плоскости пересекаются по линиям частного положения:

a) прямыми уровня;

b) проецирующими прямыми.

8. Определите линию пересечения двух плоскостей, заданных параллельными прямыми (a || b) и пересекающимися прямыми (c || d) (задать самостоятельно).

9. Определите точку пересечения прямой (общего положения) с плоскостью S (общего положения.)

Глава 5. Способы преобразования проекций

Преобразование проекций используется для наиболее выгодного изображения геометрических фигур при их исследовании и решение методических и позиционных задач. В итоге при преобразовании чертежа объекты занимают частное положение относительно плоскостей проекций. Существуют несколько способов преобразования.

- способ замены плоскостей проекций.

- способ вращения вокруг проецирующих прямых и прямых уровня.

- способ плоскопараллельного перемещения.

Принципиальная разница первого способа (замены плоскостей проекций) в том, что объект не меняет своего положения в пространстве, а вводятся новые дополнительные плоскости проекций. При использовании способов вращения и плоскопараллельного перемещения – система плоскостей остаётся неизменной, а объект перемещается относительно системы плоскостей.

Дата добавления: 2015-06-29