Проверка существенности линейной корреляционной связи

Методическая разработка

для студентов фармацевтического факультета

к практическому занятию по теме:

между двумя случайными величинами»

1. Научно - методическое обоснование темы:

В прикладных задачах часто требуется по наблюдениям выборки высказать некоторое суждение (гипотезу) относительно интересующих экспериментатора характеристик генеральной совокупности, из которой эта выборка извлечена.

В таких случаях говорят, что речь идет о проверке статистических гипотез.

Правила, согласно которым выясняется, соответствует или нет интересующая нас гипотеза опытным данным, называются статистическими критериями или просто критериями. Они дают возможность экспериментатору найти разумный ответна вопрос, подобный следующему.

В двух однородных группах больных гриппом, одной из которых проведена вакцинация средством А, а другой — средством В, среднее время выздоровления неодинаково. Указывает ли это обстоятельство на то, что одно противогриппозное средство по эффективности превосходит другое или же выявленное различие случайно?

Пусть случайная величина X является интересующей нас характеристикой генеральной совокупности и мы хотим по наблюдениям выборки подтвердить или опровергнуть некоторую гипотезу, скажем о виде функции распределения этой случайной величины. Такая гипотеза носит название нулевой гипотезы и обозначается H₀.

Наряду с гипотезой H₀ необходимо также рассмотреть конкурирующую гипотезу Н₁, которая является альтернативной по отношению к H₀, т. е. принимается в том случае, если Н₁ не верна.

2. Краткая теория:

Выборочный коэффициент линейной корреляции r_в, является точечной оценкой генерального коэффициента r и в общем случае отличается от него по величине.

В частности, выборочный коэффициент корреляции вследствие случайности выборки может оказаться отличным от нуля даже в отсутствие линейной корреляционной зависимости между изучаемыми величинами X и Y в генеральной совокупности пар их значений, т.е. когда генеральный коэффициент линейной корреляции r равен нулю. Вследствие этого после вычисления по результатам наблюдений выборочного коэффициента линейной корреляции r_в необходимо убедиться в том, что отличие его от нуля не является случайным, а отражает то обстоятельство, что и соответствующий генеральный коэффициент линейной корреляции не равен нулю. Т.е., возникает необходимость проверки гипотезы о существовании линейной корреляционной зависимости между изучаемыми величинами X и У в генеральной совокупности пар их значений, или, по-другому, гипотезы о значимости выборочного коэффициента корреляции.

Для этого в предположении нормальности двумерного распределения величин X и Y вычисляют экспериментальное значение критерия t:

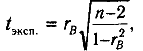(1)

где п — объем выборки (количество экспериментальных пар значений X и Y.)

Далее по таблице критических значений распределения Стьюдента (двусторонняя критическая область) при заданном (или выбранном) уровне значимости р (связанном с доверительной вероятностью γ соотношением

р =1 — γ) и числе степеней свободы f = п — 2 находят соответствующее критическое значение t_крит(p, f) распределения Стьюдента.

Правило:

1.Если окажется справедливым соотношение | t_эксп | > t_крит, то при уровне значимости р (или, что то же самое, при доверительной вероятности γ = 1 — р) делают вывод о значимости выборочного коэффициента корреляции (т.е. о неслучайности его отличия от нуля).

2. Если же | t_эксп | < t_крит, то при заданном уровне значимости такого вывода сделать нельзя.

Пример. При уровне значимости р = 0,05 проверить гипотезу о значимости выборочного коэффициента корреляции r_в ≈ 0,97 между диаметром пыльцы шаровидной фуксии и количеством пор, расположенных в экваториальной плоскости пылинки, полученного по выборке объемом n = 50.

Решение. По формуле (1) найдем экспериментальное значение критерия

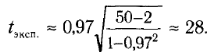
По таблице критических значений распределения Стьюдента (двусторонняя критическая область) при уровне значимости р=0,05 и числе степеней свободы f = 48 находим соответствующее критическое значение t_крит = 2,0.

Поскольку в нашем случае | t_эксп | > t_крит, при уровне значимости р = 0,05 следует сделать вывод о значимости выборочного коэффициента корреляции, т.е. о наличии линейной корреляционной зависимости диаметра пыльцы шаровидной фуксии от количества пор, расположенных в экваториальной плоскости пылинки.

3. Цель деятельности студентов на занятии:

Студент должен знать:

1.Понятия статистической гипотезы, статистического критерия, нулевой и конкурирующей гипотез.

2.Формулы для генерального и выборочного коэффициентов линейной корреляции.

3.Формулу для экспериментального значения критерия при проверке значимости выборочного коэффициента линейной корреляции.

3.Алгоритм проверки существенности линейной корреляционной связи между двумя случайными величинами.

Студент должен уметь:

Проверять значимость выборочного коэффициента линейной корреляции.

4. Содержание обучения:

Теоретическая часть:

1.Необходимость проверки гипотезы о значимости выборочного коэффициента корреляции.

2.Алгоритм проверки существенности линейной корреляционной связи между двумя случайными величинами.

Практическая часть:

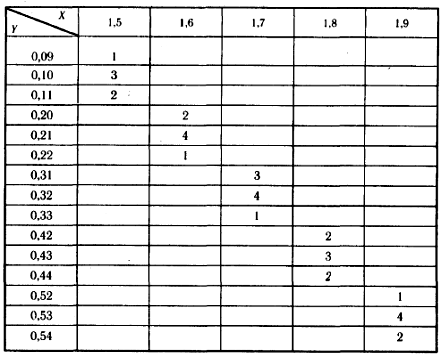
1.При уровне значимости p =0,05 проверить значимость выборочного коэффициента линейной корреляции r_в между оптической плотностью раствора Y и концентрацией растворенного в нем вещества X, рассчитанного по данным следующей корреляционной таблицы:

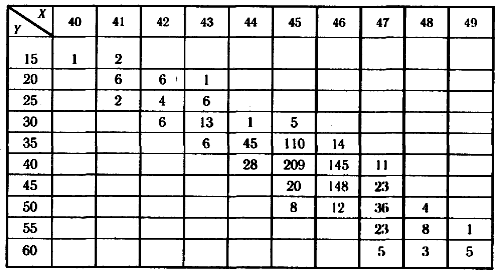
2.При уровне значимости p =0,05 проверить значимость выборочного коэффициента линейной корреляции r_в между массой Y растений некоторого вида и их высотой X, рассчитанного поданным следующей корреляционной таблицы:

5.Перечень вопросов для проверки уровня знаний:

1.Вследствие чего выборочный коэффициент линейной корреляции может оказаться отличным от нуля при отсутствии линейной корреляционной связи между изучаемыми величинами в генеральной совокупности пар их значений?

2.Приведите формулу для экспериментального значения критерия при проверке значимости выборочного коэффициента линейной корреляции.

3.Каков алгоритм проверки значимости выборочного коэффициента корреляции? Приведите соответствующее правило.

6. Хронокарта учебного занятия:

1. Организационный момент – 5 мин.

2. Разбор темы – 20 мин.

3.Решение ситуационных задач - 40 мин.

4. Текущий контроль знаний -30 мин.

5. Подведение итогов занятия – 5 мин.

7. Перечень учебной литературы к занятию:

1. Морозов Ю.В. Основы высшей математики и статистики. М., «Медицина», 2004, § 11.1..

2. Павлушков И.В. и др. Основы высшей математики и математической статистики. М., «ГЭОТАР-Медиа», 2006, § 8.5.

Дата добавления: 2015-06-30