Главные площадки и главные напряжения

Нормальные и касательные напряжения на наклонной площадке зависят от ее положения, то есть от направляющих косинусов l, m, n.

Площадки, на которых касательные напряжения равны нулю и действуют только нормальные напряжения, называются главными. Нормальные напряжения на этих площадках называются главными напряжениями.

Предположим, что наклонная площадка с направляющими косинусами l, m, n является главной, то есть вектор нормали к наклонной площадке совпадает с вектором полного напряжения. Тогда нормальное напряжение на этой площадке равно полному напряжению, а касательное напряжение равно нулю (рис.22). Проекции полного напряжения на координатные оси равны:

P_x = s×l, P_у = s×m, P_z = s×n.

Рис.22

Используя выражения, полученные для наклонной площадки, - (31) и (32), имеем:

P_x = s_x×l + t_yx×m + t_zx×n = s×l,

P_у = t_xy×l + s_y×m + t_zy×n = s×m,

P_z = t_xz×l + t_yz×m + s_z×n = s×n.

В данных уравнениях четыре неизвестных (направляющие косинусы l, m, n и главное напряжение s), поэтому необходимо четвертое уравнение:

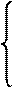(s_x - s)×l + t_yx×m + t_zx×n = 0

t_xy×l + (s_y - s)×m + t_zy×n = 0 (35)

t_xz×l + t_yz×m + (s_z - s)×n = 0

l² + m² + n² = 1

Система уравнений имеет ненулевое решение (нулевое не устраивает из-за четвертого уравнения системы), когда равен нулю главный определитель системы:

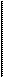
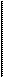s_x - s t_yx t_zx

t_xy s_y - s t_zy = 0 (36)

t_xz t_yz s_z - s

Раскроем определитель

(s_x - s)×(s_y - s)×(s_z - s) + t_yx×t_zy×t_xz + t_xy×t_yz×t_zx - t_xz×(s_y - s)×t_zx - t_xy×t_yx×(s_z - s) -

- t_yz×t_zy×(s_x - s) = 0.

s_x×s_y×s_z - s×s_y×s_z - s_x×s×s_z + s²×s_z - s_x×s×s_у + s²×s_у + s²×s_х - s³ + 2×t_xy×t_yz×t_zx –

- s_y×t_xz² + s×t_xz² - s_z×t_xу² + s×t_xу² - s_х×t_уz² + s×t_уz² = 0.

Сгруппируем слагаемые по степеням главного напряжения

- s³ + s²×(s_x + s_y + s_z) - s×(s_y×s_z + s_x×s_z + s_x×s_у - t_xz² - t_xу² - t_уz²) +

+ (s_x×s_y×s_z + 2×t_xy×t_yz×t_zx - s_y×t_xz² - s_z×t_xу² - s_х×t_уz²₎ = 0.

Запишем это уравнение в более компактной форме

s³ – I₁×s² + I₂×s – I₃ = 0 (37)

где I₁ = s_x + s_y + s_z,

I₂ = s_y×s_z + s_x×s_z + s_x×s_у - t_xz² - t_xу² - t_уz²,

I₃ = s_x×s_y×s_z + 2×t_xy×t_yz×t_zx - s_y×t_xz² - s_z×t_xу² - s_х×t_уz².

Введенные обозначения называются инвариантами напряженного состояния. Так как главные напряжения в точке являются физической характеристикой, то они не зависят от выбора системы координат, а, следовательно, и значения инвариантов также не зависят от выбора системы координат.

Решая кубическое уравнение (37), получим три вещественных корня – три главных напряжения, которые нумеруются в порядке убывания: s₁ ³ s₂ ³ s₃. Подставляя величину главного напряжения в систему (35), можно определить положение главной площадки, т.е. определить ее направляющие косинусы. Три главных площадки в точке взаимно перпендикулярны.

Дата добавления: 2015-06-30