Необходимые теоретические сведения. Методические указания к решению задачи К4.4

Методические указания к решению задачи К4.4

Для стержней, работающих на сжатие, возможна потеря несу­щей способности вследствие их изгиба, т.е. потери устойчивости. По­теря устойчивости очень опасное явление, которое, если оно проис­ходит, приводит к тяжелым последствиям. Поэтому расчёты стерж­ней на устойчивость являются чрезвычайно важными. Стержень те­ряет устойчивость в том случае, если сжимающая сила превышает некоторое критическое значение.

Впервые формулу для определения критической силы Р_{к р} полу­чил российский учёный Л. Эйлер в середине XVIII века

.

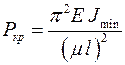(4.4)

Здесь Е – модуль упругости материала стержня; J _min – меньший из главных центральных моментов инерции; l – длина стержня; m – ко­эффициент приведения длины стержня, зависящий от условий закре­пле­ния стержня, его численное значение берут из справочников.

На рис. 27 приведены значения m для расчетных схем к за­даче 4.4.

m = 1 m = 2 m = 0,7 m = 0,5

Рис. 27

Склонность стержня к потере устойчивости характеризуется его гибкостью l, которая определяется по формуле

.

(4.5)

где – минимальный радиус инерции сечения бруса, ; F – площадь поперечного сечения.

В связи с тем, что в формулу Эйлера входит Е – модуль упруго­сти (коэффициент пропорциональности между напряжением и де­формацией), то использовать её можно только для стержней, которые теряют устойчивость при напряжениях, не превышающих s_пц – пре­дела пропорциональности материала, или у которых гибкость l больше или равна предельной гибкости l_пред. По физическому смыслу l_пред есть гибкость стержня, который теряет устойчивость при напря­же­ниях, равных s_пц, и является характеристикой материала. Значения l_пред для различных материалов приводятся в справочниках. В инже­нерных расчетах для всех сталей можно брать l_пред = 100.

Однако в некоторых инженерных конструкциях применяются такие стержни, которые могут потерять устойчивость при напряже­ниях превышающих s_пц. В этом случае предельное напряжение опре­деляется по формуле, ко­торую предложил российский инженер и ученый Ф.С. Ясинский

.

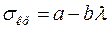(4.6)

С учетом формулы (4.6)

.

(4.7)

Здесь а, b – эмпирические коэффициенты, имеющие размерность на­пря­жений, численное значение которых для различных материалов при­ведено в справочниках. Для стали Ст. 3 а = 310 МПа, b = =1,14 МПа.

При некоторых значениях l s_кр = s_Т (т.е. пределу текучести). Это зна­чение l обозначается как l₀ и называется начальной гибкостью, l₀ может быть определена исходя из формулы (4.6).

.

Так, для стали Ст. 3 s_Т = 240 МПа, тогда получим

.

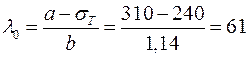При l < l₀ расчет на устойчивость не производится. Стержни с та­кой гибкостью называются стержнями малой гибкости и расcчитыва­ются на сжатие. Однако для единообразия расчета и в этом случае можно считать

.

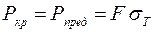(4.8)

Здесь Р_пред – предельная сила из расчета на сжатие.

Для обеспечения надежной работы сжатых стержней сила при­кладываемая к стержню должна быть меньше, чем Р_кр. С этой целью вводится коэффициент запаса по устойчивости n_y (n_y > 1).

Тогда условие устойчивости можно выразить зависимостью

.

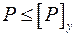(4.9)

Здесь – допускаемая сила по условию устойчивости.

,

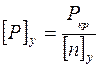(4.10)

где – нормативный коэффициент запаса по устойчивости.

4.4.2. Алгоритм определения Р_кр и [Р] _у с использованием

Дата добавления: 2015-06-30